Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ouwehand, P.
2009.
Algebraically closed algebras in certain small congruence distributive varieties.
Algebra universalis,
Vol. 61,
Issue. 2,
p.
247.

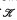 be an elementary class closed under updirected unions (e.g., if
be an elementary class closed under updirected unions (e.g., if 