Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T19:47:21.972Z Has data issue: false hasContentIssue false
  • English
  • Français

A finitary metalanguage for extended basic logic

Published online by Cambridge University Press:  12 March 2014

John Myhill
John Myhill*
Affiliation:
Temple University
Get access Rights & Permissions [Opens in a new window]

Extract

In a series of five papers, Fitch has constructed a system of combinatory logic K′ which is adequate for much of classical analysis, and is demonstrably consistent if we assume the validity of transfinite induction up to a certain ordinal (at present undetermined). The system has the following peculiarities:

1.1. It is non-finitary, i.e. the class of Gödel-numbers of its theorems does not form the range of values of any recursive function (nor, as a matter of fact, of any function definable in elementary number theory).

1.2. It does not permit quantification over real numbers; i.e. it contains no theorems of the form

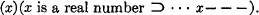
1.3. Because of 1.1, we cannot, except in trivial cases, construct actual proofs in K′; we have to resort to a metalanguage (of undetermined strength) in order to show that certain formulae are theorems of K′. Also because of 1.2, many important theorems of classical mathematics are not forthcoming in K′ itself, but only in the aforementioned metalanguage, e.g. in the form

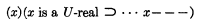
where ‘x’ is a syntactical rather than a numerical variable, a U-real is an expression of K′ rather than a number, and ‘ … x– – –’ ascribes a syntactical rather than a real number-theoretic property to x.

The purpose of this paper is to construct a finitary metalanguage for K′ in which all of Fitch's important theorems may be proved.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 17 , Issue 3 , September 1952 , pp. 164 - 178
Copyright
Copyright © Association for Symbolic Logic 1952

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Chwistek, L.. The limits of science, New York, 1948.Google Scholar
[2]Fitch, F. B.. A basic logic, this Journal, vol. 7 (1942), pp. 105–114.Google Scholar
[3]Fitch, F. B.. Representations of calculi, this Journal, vol. 9 (1944), pp. 57–62.Google Scholar
[4]Fitch, F. B.. An extension of basic logic, this Journal, vol. 13 (1948), pp. 95–106.Google Scholar
[5]Fitch, F. B.. The Heine-Borel theorem in extended basic logic, this Journal, vol. 14 (1949), pp. 9–15.Google Scholar
[6]Fitch, F. B.. A demonstrably consistent mathematics—part I, this Journal, vol. 15 (1950), pp. 17–24.Google Scholar
[7]Fitch, F. B.. A further consistent extension of basic logic, this Journal, vol. 14 (1949), pp. 209–218.Google Scholar
[8]Hetper, W.. Semantische Arithmetik, Sprawozdania Towarzystwa Naukowego Warszawskiego, vol. 27 (1934), part 3, pp. 17–24.Google Scholar
[9]Kemeny, J. G.. Type theory vs. set theory. (Speech at meeting of the Association for Symbolic Logic, Worcester, Mass., 12 1949.) An abstract appears in this Journal, vol. 15 (1950), p. 78.Google Scholar
[10]Martin, R. M.. A homogeneous system for formal logic, this Journal, vol. 8 (1943), pp. 1–23.Google Scholar
[11]Myhill, J. R.. Note on an idea of Fitch, this Journal, vol. 14 (1949), pp. 175–6.Google Scholar
[12]Novak, I. L.. The relative consistency of von Neumann's and Zermelo's axioms for set theory. (Dissertation for the degree of Ph.D. at Radcliffe College, 1948; on file in Harvard University Library.)Google Scholar
[13]Novak, I. L.. The relative consistency of von Neumann's and Zermelo's axioms for set theory. (Speech at meeting of the Association for Symbolic Logic, Columbus, Ohio, 12 1948.) An abstract appears in this Journal, vol. 14 (1949), p. 79.Google Scholar
[14]Quine, W. V.. Mathematical logic, New York, 1940.Google Scholar
[15]Quine, W. V.. Concatenation as a basis for arithmetic, this Journal, vol. 11 (1946), pp. 105–114.Google Scholar
[16]Tarski, A.. Der Wahreitsbegriff in den formalisierten Sprachen. Studio philosophica, vol. 1 (1936), pp. 261–405.Google Scholar
[17]Wang, H.. Possibilities of proving relative consistency. (Speech at meeting of the Association for Symbolic Logic, Worcester, Mass., 12 1949.) An abstract appears in this Journal, vol. 15 (1950), p. 77.Google Scholar
[18]Wang, H.. A formal system of logic, this Journal, vol. 15 (1950), pp. 25–32.Google Scholar