Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T18:31:11.921Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite sets and frege structures

Published online by Cambridge University Press:  12 March 2014

John L. Bell
John L. Bell*
Affiliation:
Department of Philosophy, Talbot College, The University of Western Ontario, London, Ontario., CanadaN6A 3K7, E-mail: jbell@julian.uwo.ca
Get access Rights & Permissions [Opens in a new window]

Extract

Call a family 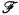of subsets of a set E inductive if 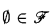and 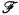is closed under unions with disjoint singletons, that is, if

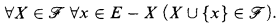
A Frege structure is a pair (E, ν) with ν a map to E whose domain dom(ν) is an inductive family of subsets of E such that

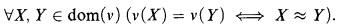
In [2] it is shown in a constructive setting that each Frege structure determines a subset which is the domain of a model of Peano's axioms. In this note we establish, within the same constructive setting, three facts. First, we show that the least inductive family of subsets of a set E is precisely the family of decidable Kuratowski finite subsets of E. Secondly, we establish that the procedure presented in [2] can be reversed, that is, any set containing the domain of a model of Peano's axioms determines a map which turns the set into a minimal Frege structure: here by a minimal Frege structure is meant one in which dom(ν) is the least inductive family of subsets of E. And finally, we show that the procedures leading from minimal Frege structures to models of Peano's axioms and vice-versa are mutually inverse. It follows that the postulation of a (minimal) Frege structure is constructively equivalent to the postulation of a model of Peano's axioms.

All arguments will be formulated within constructive (intuitionistic) set theory.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 64 , Issue 4 , December 1999 , pp. 1552 - 1556
Copyright
Copyright © Association for Symbolic Logic 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bell, John L., Toposes and local set theories: An introduction, Oxford University Press, 1988.Google Scholar
[2]Bell, John L., Frege's theorem in a constructive setting, this Journal, vol. 64 (1999), no. 2, pp. 486–488.Google Scholar