Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T17:32:28.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Flipping properties in arithmetic

Published online by Cambridge University Press:  12 March 2014

L. A. S. Kirby
L. A. S. Kirby*
Affiliation:
Princeton University, Princeton, New Jersey 08540
Get access Rights & Permissions [Opens in a new window]

Extract

Flipping properties were introduced in set theory by Abramson, Harrington, Kleinberg and Zwicker [1]. Here we consider them in the context of arithmetic and link them with combinatorial properties of initial segments of nonstandard models studied in [3]. As a corollary we obtain independence resutls involving flipping properties.

We follow the notation of the author and Paris in [3] and [2], and assume some knowledge of [3]. M will denote a countable nonstandard model of P (Peano arithmetic) and I will be a proper initial segment of M. We denote by N the standard model or the standard part of M. X ↑ I will mean that X is unbounded in I. If X ⊆ M is coded in M and M ≺ K, let X(K) be the subset of K coded in K by the element which codes X in M. So X(K) ⋂ M = X.

Recall that M ≺IK (K is an I-extension of M) if M ≺ K and for some c∈K,

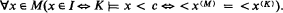
In [3] regular and strong initial segments are defined, and among other things it is shown that I is regular if and only if there exists an I-extension of M.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 47 , Issue 2 , June 1982 , pp. 416 - 422
Copyright
Copyright © Association for Symbolic Logic 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Abramson, F. G., Harrington, L. A., Kleinberg, E. M. and Zwicker, W. S., Flipping properties: A unifying thread in the theory of large cardinals, Annals of Mathematical Logic, vol. 12 (1977), pp. 25–58.CrossRefGoogle Scholar
[2]Kirby, L. A. S., Ph. D. Thesis, Manchester, 1977.Google Scholar
[3]Kirby, L. A. S. and Paris, J. B., Initial segments of models of Peano's axioms, Set theory and hierarchy theory. V, Lecture Notes in Mathematics, vol. 619, Springer-Verlag, Berlin and New York, 1977, pp. 211–226.CrossRefGoogle Scholar
[4]Mints, G. E., Quantifier-free and one-quantifier systems, Journal of Soviet Mathematics, vol. 1 (1) (1973), pp. 71–84.CrossRefGoogle Scholar
[5]Paris, J. B., Some independence results for Peano arithmetic, this Journal, vol. 43 (1978), pp. 725–731.Google Scholar
[6]Paris, J. B., A hierarchy of cuts in models of arithmetic, Proceedings of the 1979 Karpacz Conference, North-Holland, Amsterdam, pp. 312–332.Google Scholar
[7]Paris, J. B. and Kirby, L. A. S., Σn-collection Schemas in arithmetic, Logic Colloquium '77, North-Holland, Amsterdam, 1978, pp. 199–210.CrossRefGoogle Scholar