Article contents
FORCING AXIOMS AND THE DEFINABILITY OF THE NONSTATIONARY IDEAL ON THE FIRST UNCOUNTABLE
Part of:
Set theory
Published online by Cambridge University Press: 19 June 2023
Abstract
We show that under 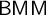 $\mathsf {BMM}$ and “there exists a Woodin cardinal,
$\mathsf {BMM}$ and “there exists a Woodin cardinal, $"$ the nonstationary ideal on
$"$ the nonstationary ideal on 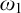 $\omega _1$ cannot be defined by a
$\omega _1$ cannot be defined by a 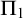 $\Pi _1$ formula with parameter
$\Pi _1$ formula with parameter 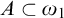 $A \subset \omega _1$. We show that the same conclusion holds under the assumption of Woodin’s
$A \subset \omega _1$. We show that the same conclusion holds under the assumption of Woodin’s  $(\ast )$-axiom. We further show that there are universes where
$(\ast )$-axiom. We further show that there are universes where 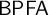 $\mathsf {BPFA}$ holds and
$\mathsf {BPFA}$ holds and 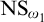 $\text {NS}_{\omega _1}$ is
$\text {NS}_{\omega _1}$ is 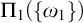 $\Pi _1(\{\omega _1\})$-definable. Lastly we show that if the canonical inner model with one Woodin cardinal
$\Pi _1(\{\omega _1\})$-definable. Lastly we show that if the canonical inner model with one Woodin cardinal 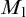 $M_1$ exists, there is a generic extension of
$M_1$ exists, there is a generic extension of 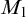 $M_1$ in which
$M_1$ in which 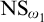 $\text {NS}_{\omega _1}$ is saturated and
$\text {NS}_{\omega _1}$ is saturated and 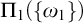 $\Pi _1(\{ \omega _1\} )$-definable, and
$\Pi _1(\{ \omega _1\} )$-definable, and 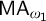 $\mathsf {MA_{\omega _1}}$ holds.
$\mathsf {MA_{\omega _1}}$ holds.
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
Bagaria, J.,
Generic absoluteness and forcing axioms
,
Models, Algebras, and Proofs
(X. Caicedo and C. H. Montenegro, editors), Lecture Notes in Pure and Applied Mathematics, vol. 203, Dekker, New York, 1999, pp. 1–12.Google Scholar
Caicedo, A. and Velickovic, B.,
The bounded proper forcing axiom and well orderings of the reals
.
Mathematical Research Letters
, vol. 13 (2006), nos. 2–3, pp. 393–408.CrossRefGoogle Scholar
Foreman, M. and Magidor, M., Mutually stationary sequences of sets and the non-saturation of the non-stationary ideal on
 ${P}_{\kappa}(\lambda)$
.
Acta Mathematica
, vol. 186 (2001), no. 2, pp. 271–300.CrossRefGoogle Scholar
${P}_{\kappa}(\lambda)$
.
Acta Mathematica
, vol. 186 (2001), no. 2, pp. 271–300.CrossRefGoogle Scholar
Goldstern, M. and Shelah, S.,
The bounded proper forcing axiom
, this Journal, vol. 60 (1995), no. 1, pp. 58–73.Google Scholar
Harrington, L.,
Long projective wellorderings
.
Annals of Mathematical Logic
, vol. 12 (1977), no. 1, pp. 1–24.CrossRefGoogle Scholar
Hoffelner, S.,
 ${NS}_{\omega_1}$
${NS}_{\omega_1}$
 ${\varDelta}_1$
-definable and saturated
, this Journal, vol. 86 (2021), no. 1, pp. 25–59.Google Scholar
${\varDelta}_1$
-definable and saturated
, this Journal, vol. 86 (2021), no. 1, pp. 25–59.Google Scholar
Hoffelner, S., Larson, P. B., Schindler, R., and Wu, L.,
 $\mathsf{PFA}$
and the definability of the nonstationary ideal, in preparation.Google Scholar
$\mathsf{PFA}$
and the definability of the nonstationary ideal, in preparation.Google Scholar
Jech, T.,
Set Theory: The Third Millennium Edition
, Springer, Berlin–Heidelberg, 2003.Google Scholar
Larson, P. B.,
The Stationary Tower. Notes on a Course by W. Hugh Woodin
, University Lecture Series, vol. 32, American Mathematical Society, Providence, 2004.Google Scholar
Larson, P. B.,
Forcing over models of determinacy
,
Handbook of Set Theory
(Foreman, M. and Kanamori, A., editors), Springer, Dordrecht, 2010, pp. 2121–2177.CrossRefGoogle Scholar
Lücke, P., Schindler, R., and Schlicht, P.,
 ${\varSigma}_1(\kappa)$
-definable subsets of
${\varSigma}_1(\kappa)$
-definable subsets of
 $H({\kappa}^{+})$
, this Journal, vol. 82 (2017), no. 3, pp. 1106–1131.Google Scholar
$H({\kappa}^{+})$
, this Journal, vol. 82 (2017), no. 3, pp. 1106–1131.Google Scholar
Miyamoto, T.,
On iterating semiproper preorders
, this Journal, vol. 67 (2002), pp. 1431–1468.Google Scholar
Moore, J. T.,
Set mapping reflection
.
Journal of Mathematical Logic
, vol. 5 (2005), no. 1, pp. 87–97.CrossRefGoogle Scholar
Schindler, R. and Sun, X.,
 $\mathsf{MM}$
and the definability of
$\mathsf{MM}$
and the definability of
 ${\mathrm{NS}}_{\omega_1}\kern-1.2pt$
, preprint, 2022.Google Scholar
${\mathrm{NS}}_{\omega_1}\kern-1.2pt$
, preprint, 2022.Google Scholar
Shelah, S.,
Proper and Improper Forcing
, second ed., Perspectives in Mathematical Logic, vol. 5, Springer, Berlin, 1998, xlviii + 1020 pp.CrossRefGoogle Scholar
Taylor, A.,
Regularity properties of ideals and ultrafilters
.
Annals of Mathematical Logic
, vol. 16 (1979), pp. 33–55.CrossRefGoogle Scholar
Todorcevic, S.,
Localized reflection and fragments of PFA
,
Set Theory (Piscataway, NJ, 1999)
(S. Thomas, editor), DIMACS Series in Discrete Mathematics and Theoretical Computer Science, vol. 58, American Mathematics Society, Providence, 2002, pp. 135–148.CrossRefGoogle Scholar
Todorcevic, S.,
Generic absoluteness and the continuum
.
Mathematical Research Letters
, vol. 9 (2002), no. 4, 465–471.CrossRefGoogle Scholar
Woodin, H. W.,
The Axiom of Determinacy, Forcing Axioms, and the Nonstationary Ideal
, De Gruyter, Berlin–New York, 2001.Google Scholar
- 1
- Cited by


