Hostname: page-component-7dd5485656-wlg5v Total loading time: 0 Render date: 2025-10-28T16:35:19.420Z Has data issue: false hasContentIssue false
  • English
  • Français

A FORCING NOTION COLLAPSING 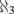$\aleph _3 $ AND PRESERVING ALL OTHER CARDINALS

Published online by Cambridge University Press:  21 December 2018

DAVID ASPERÓ
DAVID ASPERÓ*
Affiliation:
SCHOOL OF MATHEMATICS UNIVERSITY OF EAST ANGLIA NORWICH, NR4 7TJ, UKE-mail:d.aspero@uea.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

I construct, in ZFC, a forcing notion that collapses 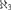$\aleph _3 $ and preserves all other cardinals. The existence of such a forcing answers a question of Uri Abraham from 1983.

Keywords

03E40collapsing ℵ3Bamgartner clubstwo-type chains of modelspartial square sequences

Information

Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 4 , December 2018 , pp. 1579 - 1594
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Abraham, U., On forcing without the continuum hypothesis, this Journal, vol. 48 (1983), no. 3, pp. 658–661.Google Scholar
Asperó, D., Adding many Baumgartner clubs. Archive for Mathematical Logic, vol. 56 (2017), no. 7–8, pp. 797–810.CrossRefGoogle Scholar
Baumgartner, J. E., Applications of the proper forcing axiom, Handbook of Set Theoretic Topology (Kunen, K. and Vaughan, J. E., editors), North Holland, Amsterdam, 1984, pp. 913–959.CrossRefGoogle Scholar
Dolinar, G. and Džamonja, M., Forcing $\square _{\omega _1 } $ with finite conditions. Annals of Pure and Applied Logic , vol. 164 (2013), no. 1, pp. 49–64.CrossRefGoogle Scholar
Jech, T., Set Theory, Springer, Berlin, 2002.Google Scholar
Krueger, J., Coherent adequate sets and forcing square. Fundamenta Mathematicae, vol. 224 (2014), pp. 279–300.CrossRefGoogle Scholar
Kunen, K., Set Theory, An Introduction to Independence Proofs, North-Holland, Amsterdam, 1980.Google Scholar
Magidor, M., Reflecting stationary sets, this Journal, vol. 47 (1982), no. 4, pp. 755–771.Google Scholar
Neeman, I., Forcing with sequences of models of two types. Notre Dame Journal of Formal Logic, vol. 55 (2014), pp. 265–298.CrossRefGoogle Scholar
Neeman, I., Two applications of finite side conditions at ω2. Archive for Mathematical Logic, vol. 56 (2017), no. 7–8, pp. 983–1036.CrossRefGoogle Scholar
Shelah, S., Reflecting stationary sets and successors of singular cardinals. Archive for Mathematical Logic, vol. 31 (1991), no. 1, pp. 25–53.CrossRefGoogle Scholar
Shelah, S., Cardinal Arithmetic, Oxford University Press, London, 1994.Google Scholar
Todorčević, S., A note on the proper forcing axiom, Axiomatic Set Theory (Baumgartner, J. E., Martin, D. A., and Shelah, S., editors), Contemporary Mathematics, American Mathematical Society, Providence, RI, 1984, pp. 209–218.CrossRefGoogle Scholar