Article contents
A form of feasible interpolation for constant depth Frege systems
Published online by Cambridge University Press: 12 March 2014
Abstract
Let L be a first-order language and Φ and Ψ two 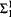 L-sentences that cannot be satisfied simultaneously in any finite L-structure. Then obviously the following principle ChainL,Φ,Ψ(n, m) holds: For any chain of finite L-structures C1, …, Cm with the universe [n] one of the following conditions must fail:
L-sentences that cannot be satisfied simultaneously in any finite L-structure. Then obviously the following principle ChainL,Φ,Ψ(n, m) holds: For any chain of finite L-structures C1, …, Cm with the universe [n] one of the following conditions must fail:
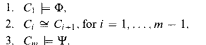
For each fixed L and parameters n, m the principle ChainL,Φ,Ψ(n,m) can be encoded into a propositional DNF formula of size polynomial in n, m.
For any language L containing only constants and unary predicates we show that there is a constant CL such that the following holds: If a constant depth Frege system in DeMorgan language proves ChainL,Φ,Ψ(n, cL . n) by a size s proof then the class of finite L-structures with universe [n] satisfying Φ can be separated from the class of those L-structures on [n] satisfying ψ by a depth 3 formula of size 2log(S)O(1) and with bottom fan-in log(S)O(1).
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2010
References
REFERENCES
- 4
- Cited by

