Article contents
The foundations of Suslin logic
Published online by Cambridge University Press: 12 March 2014
Extract
Let L be a first order logic and 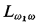 the infinitary logic (as described in [K, p. 6] over L. Suslin logic
the infinitary logic (as described in [K, p. 6] over L. Suslin logic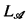 is obtained from
is obtained from 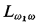 by adjoining new propositional operators
by adjoining new propositional operators 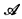 and
and 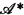 . Let f range over elements of ωω and n range over elements of ω. Seq is the set of all finite sequences of elements of ω. If θ: Seq →
. Let f range over elements of ωω and n range over elements of ω. Seq is the set of all finite sequences of elements of ω. If θ: Seq → 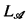 is a mapping into formulas of
is a mapping into formulas of 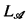 then
then 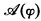 and
and 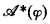 are formulas of LA . If
are formulas of LA . If 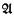 is a structure in which we can interpret
is a structure in which we can interpret 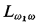 and h is an
and h is an 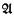 -assignment then we extend the notion of satisfaction from
-assignment then we extend the notion of satisfaction from 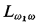 to
to 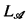 by defining
by defining
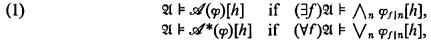
where f ∣ n is the finite sequence consisting of the first n values of f. We assume that 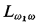 has ω symbols for relations, functions, constants, and ω1 variables. θ is
has ω symbols for relations, functions, constants, and ω1 variables. θ is 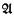 valid if
valid if 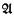 θ ⊧ [h] for every h and is valid if
θ ⊧ [h] for every h and is valid if 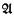 -valid for every
-valid for every 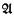 . We address ourselves to the problem of finding syntactical rules (or nearly so) which characterize validity
. We address ourselves to the problem of finding syntactical rules (or nearly so) which characterize validity 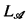 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1975
References
REFERENCES
- 4
- Cited by

