No CrossRef data available.
Article contents
FRACTAL DIMENSIONS OF k-AUTOMATIC SETS
Published online by Cambridge University Press: 25 July 2023
Abstract
This paper seeks to build on the extensive connections that have arisen between automata theory, combinatorics on words, fractal geometry, and model theory. Results in this paper establish a characterization for the behavior of the fractal geometry of “k-automatic” sets, subsets of 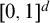 $[0,1]^d$ that are recognized by Büchi automata. The primary tools for building this characterization include the entropy of a regular language and the digraph structure of an automaton. Via an analysis of the strongly connected components of such a structure, we give an algorithmic description of the box-counting dimension, Hausdorff dimension, and Hausdorff measure of the corresponding subset of the unit box. Applications to definability in model-theoretic expansions of the real additive group are laid out as well.
$[0,1]^d$ that are recognized by Büchi automata. The primary tools for building this characterization include the entropy of a regular language and the digraph structure of an automaton. Via an analysis of the strongly connected components of such a structure, we give an algorithmic description of the box-counting dimension, Hausdorff dimension, and Hausdorff measure of the corresponding subset of the unit box. Applications to definability in model-theoretic expansions of the real additive group are laid out as well.
Keywords
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic


