No CrossRef data available.
Article contents
Frege proof system and TNC°
Published online by Cambridge University Press: 12 March 2014
Extract
A Frege proof system F is any standard system of prepositional calculus, e.g., a Hilbert style system based on finitely many axiom schemes and inference rules. An Extended Frege system EF is obtained from F as follows. An EF-sequence is a sequence of formulas ψ1, …, ψκ such that eachψi is either an axiom of F, inferred from previous ψu and ψv (= ψu → ψi ) by modus ponens or of the form q ↔ φ, where q is an atom occurring neither in φ nor in any of ψ1,…,ψi−1. Such q ↔ φ, is called an extension axiom and q a new extension atom. An EF-proof is any EF-sequence whose last formula does not contain any extension atom. In [12], S. A. Cook and R. Reckhow proved that the pigeonhole principle PHP has a simple polynomial size EF-proof and conjectured that PHP does not admit polynomial size F-proof. In [5], S. R. Buss refuted this conjecture by furnishing polynomial size F-proof for PHP. Since then the important separation problem of polynomial size F and polynomial size EF has not shown any progress.
In [11], S. A. Cook introduced the system PV, a free variable equational logic whose provable functional equalities are ‘polynomial time verifiable’ and showed that the metamathematics of F and EF can be developed in PV and the soundness of EF proved in PV. In [3], S. R. Buss introduced the first order system 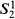 and showed that
and showed that 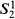 is essentially a conservative extension of PV. There he also introduced a second order system
is essentially a conservative extension of PV. There he also introduced a second order system  (BD).
(BD).
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1998

