Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Downey, Rod
2012.
How the World Computes.
Vol. 7318,
Issue. ,
p.
162.
Downey, Rod
2014.
Turing's Legacy.
p.
90.
Sureson, Claude
2015.
Random reals as measures of natural open sets.
Theoretical Computer Science,
Vol. 589,
Issue. ,
p.
1.
BECHER, VERÓNICA
and
GRIGORIEFF, SERGE
2015.
Wadge hardness in Scott spaces and its effectivization.
Mathematical Structures in Computer Science,
Vol. 25,
Issue. 7,
p.
1520.
Sureson, Claude
2016.
Π11-Martin-Löf random reals as measures of natural open sets.
Theoretical Computer Science,
Vol. 653,
Issue. ,
p.
26.
Barmpalias, George
Cenzer, Douglas
and
Porter, Christopher P.
2017.
The Probability of a Computable Output from a Random Oracle.
ACM Transactions on Computational Logic,
Vol. 18,
Issue. 3,
p.
1.
Barmpalias, George
Cenzer, Douglas
and
Porter, Christopher P.
2017.
Random numbers as probabilities of machine behavior.
Theoretical Computer Science,
Vol. 673,
Issue. ,
p.
1.
Barmpalias, George
and
Lewis-Pye, Andrew
2017.
Differences of halting probabilities.
Journal of Computer and System Sciences,
Vol. 89,
Issue. ,
p.
349.
Becher, Verónica
and
Grigorieff, Serge
2022.
Randomness and uniform distribution modulo one.
Information and Computation,
Vol. 285,
Issue. ,
p.
104857.

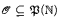 . In particular, we develop methods to transfer
. In particular, we develop methods to transfer 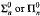 many-one completeness results of index sets to
many-one completeness results of index sets to 