Article contents
A functorial property of the Aczel-Buchholz-Feferman function
Published online by Cambridge University Press: 12 March 2014
Abstract
Let Ω be the least uncountable ordinal. Let 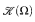 be the category where the objects are the countable ordinals and where the morphisms are the strictly monotonic increasing functions. A dilator is a functor on
be the category where the objects are the countable ordinals and where the morphisms are the strictly monotonic increasing functions. A dilator is a functor on 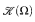 which preserves direct limits and pullbacks. Let τ < ΩE ≔ min{ξ > Ω: ξ = ωξ}. Then τ has a unique “term”-representation in Ω. λξη.ωξ + η and countable ordinals called the constituents of τ. Let δ < Ω and K(τ) be the set of the constituents of τ. Let β = max K(τ). Let [β] be an occurrence of β in τ such that τ[β] = τ. Let
which preserves direct limits and pullbacks. Let τ < ΩE ≔ min{ξ > Ω: ξ = ωξ}. Then τ has a unique “term”-representation in Ω. λξη.ωξ + η and countable ordinals called the constituents of τ. Let δ < Ω and K(τ) be the set of the constituents of τ. Let β = max K(τ). Let [β] be an occurrence of β in τ such that τ[β] = τ. Let 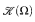 be the fixed point-free version of the binary Aczel-Buchholz-Feferman-function (which is defined explicitly in the text below) which generates the Bachman-hierarchy of ordinals. It is shown by elementary calculations that
be the fixed point-free version of the binary Aczel-Buchholz-Feferman-function (which is defined explicitly in the text below) which generates the Bachman-hierarchy of ordinals. It is shown by elementary calculations that 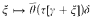 is a dilator for every γ > max{β.δ.ω}.
is a dilator for every γ > max{β.δ.ω}.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1994
References
REFERENCES
- 3
- Cited by

