Functors and ordinal notations. IV: The Howard ordinal and the functor ∧.

Extract

In this paper, we prove a result that J. Y. Girard has conjectured for the last few years. That is,

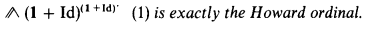
This result is part of a study of ordinal notations. For the proof, we use some concepts introduced in Parts I, II and III of this article (see [GV1], [GV2] and [V]); in particular, in Part III (see [V]) we defined the category GAR of gardens (of type Ω), and we have shown that there is an isomorphism between GAR and the category DIL Ω of dilators which send Ω into Ω. To describe this isomorphism, we defined a functor SYN from GAR to DIL Ω and a functor DEC from DIL Ω to GAR which are inverse to each other. The functor SYN is constructed by induction on the height x of the garden Jx, iterating, at each step of cofinality Ω, the operation UN (unification of variables; see [G1, Chapter 3]). Here, we define the functor S⊿ from GAR to DIL Ω: this construction is very close to that of SYN, but we iterate, at each step of cofinality Ω, the operation ⊿ (identification of variables; see [G, Chapter 3]). Technically, the definition of S⊿ is easier and more natural than that of SYN (as ⊿ is easier than UN) but is not inversible (as ⊿); for example, if we consider the (regular) garden G_εΩ+1 introduced in [GV2],S⊿(G_εΩ+1) is exactly the dilator N = ⋃_0<n<ωN_n, with N₁ = 2 + Id, and 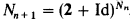, but we are incapable of expressing SYN(G_εΩ+1).