Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-10T09:24:12.203Z Has data issue: false hasContentIssue false
  • English
  • Français

Gδ Sets IN σ-IDEALS GENERATED BY COMPACT SETS

Published online by Cambridge University Press:  04 March 2019

MAYA SARAN
MAYA SARAN*
Affiliation:
DEPARTMENT OF MATHEMATICS ASHOKA UNIVERSITY RAJIV GANDHI EDUCATION CITY SONEPAT, HARYANA131029, INDIA E-mail: maya.saran@ashoka.edu.in
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a compact Polish space E and the hyperspace of its compact subsets 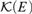${\cal K}\left( E \right)$, we consider Gδσ-ideals of compact subsets of E. Solecki has shown that any σ-ideal in a broad natural class of Gδ ideals can be represented via a compact subset of 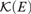${\cal K}\left( E \right)$; in this article we examine the behaviour of Gδ subsets of E with respect to the representing set. Given an ideal I in this class, we construct a representing set that recognises a compact subset of E as being “small” precisely when it is in I, and recognises a Gδ subset of E as being “small” precisely when it is covered by countably many compact sets from I.

Keywords

03E1528A0554H05descriptive set theoryideals of compact sets
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 2 , June 2019 , pp. 781 - 797
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Choquet, G., Theory of capacities. Annales de l’Institut Fourier, vol. 5 (1954), pp. 131–295.Google Scholar
Kechris, A. S., Hereditary properties of the class of closed sets of uniqueness for trigonometric series. Israel Journal of Mathematics, vol. 73 (1991), no. 2, pp. 189–198.Google Scholar
Kechris, A. S., Classical Descriptive Set Theory, Graduate Texts in Mathematics, vol. 156, Springer-Verlag, New York, 1995.Google Scholar
Kechris, A. S., Louveau, A., and Woodin, W. H., The structure of σ-ideals of compact sets. Transactions of the American Mathematical Society, vol. 301 (1987), no. 1, pp. 263–288.Google Scholar
Saran, M., A note on Gδ ideals of compact sets. Commentationes Mathematicae Universitatis Carolinae, vol. 50 (2009), no. 4, pp. 569–573.Google Scholar
Solecki, S., Covering analytic sets by families of closed set, this Journal, vol. 59 (1994), no. 3, pp. 1022–1031.Google Scholar
Solecki, S., Gδ ideals of compact sets. Journal of the European Mathematical Society, vol. 13 (2011), no. 4, pp. 853–882.Google Scholar