Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T08:14:26.459Z Has data issue: false hasContentIssue false
  • English
  • Français

A generalization of Sierpiński's paradoxical decompositions: Coloring semialgebraic grids

Published online by Cambridge University Press:  12 March 2014

James H. Schmerl
James H. Schmerl*
Affiliation:
Department of Mathematics, University of Connecticut, Storrs, CT 06269-3009, E-mail: james.schmerl@uconn.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

A structure 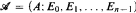is an n-grid if each Ei, is an equivalence relation on A and whenever X and Y are equivalence classes of, respectively, distinct Ei, and Ej, then X ∩ Y is finite. A coloring χ: A → n is acceptable if whenever X is an equivalence class of Ei, then {x ∈ X: χ(x) = i} is finite. If B is any set, then the n-cube Bn = (Bn; E0, …, En−1) is considered as an n-grid, where the equivalence classes of Ei are the lines parallel to the i-th coordinate axis. Kuratowski [9], generalizing the n = 3 case proved by Sierpihski [17], proved that ℝn has an acceptable coloring iff 2ℵ0 ≤ ℵn−2. The main result is: if 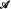is a semialgebraic (i.e., first-order definable in the field of reals) n-grid, then the following are equivalent: (1) if 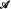embeds all finite n-cubes, then 2ℵ0 ≤ ℵn−2: (2) if 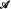embeds ℝn, then 2ℵ0 ≤ ℵn−2; (3) 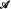has an acceptable coloring.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 77 , Issue 4 , December 2012 , pp. 1165 - 1183
Copyright
Copyright © Association for Symbolic Logic 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bagemihl, Frederick, A proposition of elementary plane geometry that implies the continuum hypothesis, Zeitschrift für Mathematische Logik and Grundlagen der Mathematik, vol. 7 (1961), pp. 77–79.CrossRefGoogle Scholar
[2]Davies, Roy O., The power of the continuum and some propositions of plane geometry, Fundamenta Mathematical, vol. 52 (1962), pp. 277–281.CrossRefGoogle Scholar
[3]Davies, Roy O., On a problem of Erdős concerning decompositions of the plane, Proceedings of the Cambridge Philosophical Society, vol. 59 (1963), pp. 33–36.CrossRefGoogle Scholar
[4]de la Vega, Ramiro, Coloring grids, preprint.Google Scholar
[5]de la Vega, Ramiro, Decompositions of the plane and the size of the continuum, Fundamenta Mathematicae, vol. 203 (2009), pp. 65–74.CrossRefGoogle Scholar
[6]Erdős, P., Jackson, S., and Mauldin, R. D., On partitions of lines and space, Fundamenta Mathematicae, vol. 145 (1994), pp. 101–119.Google Scholar
[7]Graham, R. L., Rothschild, B. L., and Spencer, J. H., Ramsey theory, Wiley & Sons, New York, 1980.Google Scholar
[8]Komjáth, Péter, Three clouds may cover the plane, Annals of Pure and Applied Logic, vol. 109 (2001), pp. 71–75.CrossRefGoogle Scholar
[9]Kuratowski, C., Sur une characterisation des alephs, Fundamenta Mathematicae, vol. 38 (1951), pp. 14–17.CrossRefGoogle Scholar
[10]Miller, Arnold, Set theory of the plane, (2005) http://www.math.wisc.edu/~miller/old/m873-05/index.html.Google Scholar
[11]Schmerl, J. H., Countable partitions of Euclidean space, Mathematical Proceedings of the Cambridge Philosophical Society, vol. 120 (1996), pp. 7–12.CrossRefGoogle Scholar
[12]Schmerl, J. H., Avoidable algebraic subsets of Euclidean space, Transactions of the American Mathematical Society, vol. 352 (2000), pp. 2479–2489.CrossRefGoogle Scholar
[13]Schmerl, J. H., How many clouds cover the plane?, Fundamenta Mathematicae, vol. 177 (2003), pp. 209–211.CrossRefGoogle Scholar
[14]Schmerl, J. H., Partitioning large vector spaces, this Journal, vol. 68 (2003), pp. 1171–1180.Google Scholar
[15]Schmerl, J. H., Covering the plane with sprays, Fundamenta Mathematicae, vol. 208 (2010), pp. 263–272.CrossRefGoogle Scholar
[16]Sierpiński, W., Sur un théoréme équivalent à l'hypothése du continu (2ℵ0 = ℵ1), Bull. Int. Acad. Polon. Lett. Cl. Sci. Math. Nat., Série A: Sciences Mathématiques, (1919), pp. 1–3.Google Scholar
[17]Sierpiński, W., Sur une propriété paradoxale de l'espace à trois dimensions équivalent à l'hypothése du continu, Rendiconti del Circolo Matematico di Palermo. Serie II, vol. 1 (1952), pp. 7–10.CrossRefGoogle Scholar
[18]Sikorski, Roman, A characterization of alephs, Fundamenta Mathematicae, vol. 38 (1951), pp. 18–22.CrossRefGoogle Scholar
[19]Simms, John C., Sierpiński's theorem, Bulletin of the Belgian Mathematical Society–Simon Stevin, vol. 65 (1991), pp. 69–163.Google Scholar
[20]Simms, John C., Another characterization of alephs: decompositions of hyperspace, Notre Dame Journal of Formal Logic, vol. 38 (1997), pp. 19–36.CrossRefGoogle Scholar
[21]van den Dries, Lou, Algebraic theories with definable skolem functions, this Journal, vol. 49 (1984), pp. 625–629.Google Scholar
[22]van den Dries, Lou, Tame topology and o-minimal structures, London Mathematical Society Lecture Note Series, vol. 248, Cambridge University Press, Cambridge, 1998.CrossRefGoogle Scholar