Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T19:18:19.356Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized interpolation theorems

Published online by Cambridge University Press:  12 March 2014

Stephen J. Garland
Stephen J. Garland*
Affiliation:
Dartmouth College, Hanover, New Hampshire 03755 University of California, Los Angeles, California 90024
Get access Rights & Permissions [Opens in a new window]

Extract

Chang [1], [2] has proved the following generalization of the Craig interpolation theorem [3]: For any first-order formulas φ and ψ with free first- and second-order variables among ν1, …, νn, R and ν1, …, νn, S respectively, and for any sequence Q1, …, Qn of quantifiers such that Q1 is universal whenever ν1 is a second-order variable, if

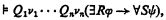
then there is a first-order formula θ with free variables among ν1, …, νn such that

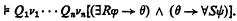
(Note that the Craig interpolation theorem is the special case of Chang's theorem in which Q1, …, Qn are all universal quantifiers.) Chang also raised the question [2, Remark (k)] as to whether the Lopez-Escobar interpolation theorem [6] for the infinitary language Lω1ω possesses a similar generalization. In this paper, we show that the answer to Chang's question is affirmative and, moreover, that several interpolation theorems for applied second-order languages for number theory also possess such generalizations.

Maehara and Takeuti [7] have established independently proof-theoretic interpolation theorems for first-order logic and Lω1ω which have as corollaries both Chang's theorem and its analog for Lω1ω. Our proofs are quite different from theirs and rely on model-theoretic techniques stemming from the analogy between the theory of definability in Lω1ω and the theory of Borel and analytic sets of real numbers, rather than the technique of cut-elimination.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 37 , Issue 2 , June 1972 , pp. 343 - 351
Copyright
Copyright © Association for Symbolic Logic 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Chang, C. C., A generalization of the Craig interpolation theorem, Notices of the American Mathematical Society, vol. 15 (1968), p. 934.Google Scholar
[2]Chang, C. C., Two interpolation theorems, Symposia Mathematica, vol. V, Academic Press, New York, 1970, pp. 5–19.Google Scholar
[3]Craig, W., Three uses of the Herbrand-Gentzen theorem in relating model theory and proof theory, this Journal, vol. 22 (1957), pp. 269–285.Google Scholar
[4]Kueker, D. W., Generalized interpolation and definability, Annals of Mathematical Logic, vol. 1 (1970), pp. 423–468.CrossRefGoogle Scholar
[5]Kuratowski, K., Topology, Academic Press, New York, 1966.Google Scholar
[6]Lopez-Escobar, E. G. K., An interpolation theorem for denumerably long sentences, Fundamenta Mathematicae, vol. 57 (1965), pp. 253–272.CrossRefGoogle Scholar
[7]Maehara, S. and Takeuti, G., Two interpolation theorems for Π11 predicate calculus, this Journal, vol. 36 (1971), pp. 262–270.Google Scholar
[8]Makkai, M., An application of the method of Smullyan to logics on admissible sets, Buttetin l'Académie Polonaise des Sciences. Série des Sciences Mathématiques, Astronomiques et Physiques, vol. 17 (1969), pp. 341–346.Google Scholar
[9]Scott, D., Logic with denumerably long formulas and finite strings of quantifiers, The theory of models, North-Holland, Amsterdam, 1965, pp. 329–341.Google Scholar
[10]Shoenfield, J. R., Mathematical logic, Addison-Wesley, Reading, Mass., 1967.Google Scholar