No CrossRef data available.
Published online by Cambridge University Press: 12 December 2014
We investigate some common points between stable structures and weakly small structures and define a structure M to be fine if the Cantor-Bendixson rank of the topological space 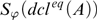 ${S_\varphi }\left( {dc{l^{eq}}\left( A \right)} \right)$ is an ordinal for every finite subset A of M and every formula
${S_\varphi }\left( {dc{l^{eq}}\left( A \right)} \right)$ is an ordinal for every finite subset A of M and every formula 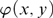 $\varphi \left( {x,y} \right)$ where x is of arity 1. By definition, a theory is fine if all its models are so. Stable theories and small theories are fine, and weakly minimal structures are fine. For any finite subset A of a fine group G, the traces on the algebraic closure
$\varphi \left( {x,y} \right)$ where x is of arity 1. By definition, a theory is fine if all its models are so. Stable theories and small theories are fine, and weakly minimal structures are fine. For any finite subset A of a fine group G, the traces on the algebraic closure 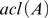 $acl\left( A \right)$ of A of definable subgroups of G over
$acl\left( A \right)$ of A of definable subgroups of G over 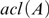 $acl\left( A \right)$ which are boolean combinations of instances of an arbitrary fixed formula can decrease only finitely many times. An infinite field with a fine theory has no additive nor multiplicative proper definable subgroups of finite index, nor Artin-Schreier extensions.
$acl\left( A \right)$ which are boolean combinations of instances of an arbitrary fixed formula can decrease only finitely many times. An infinite field with a fine theory has no additive nor multiplicative proper definable subgroups of finite index, nor Artin-Schreier extensions.