Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Eleftheriou, Pantelis E.
2013.
Non-standard lattices and o-minimal groups.
The Bulletin of Symbolic Logic,
Vol. 19,
Issue. 1,
p.
56.

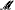 = ⟨
= ⟨