No CrossRef data available.
Article contents
A HIERARCHY ON NON-ARCHIMEDEAN POLISH GROUPS ADMITTING A COMPATIBLE COMPLETE LEFT-INVARIANT METRIC
Published online by Cambridge University Press: 06 February 2024
Abstract
In this article, we introduce a hierarchy on the class of non-archimedean Polish groups that admit a compatible complete left-invariant metric. We denote this hierarchy by 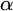 $\alpha $-CLI and L-
$\alpha $-CLI and L-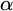 $\alpha $-CLI where
$\alpha $-CLI where 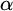 $\alpha $ is a countable ordinal. We establish three results:
$\alpha $ is a countable ordinal. We establish three results:
(1) G is
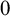 $0$-CLI iff
$0$-CLI iff 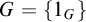 $G=\{1_G\}$;
$G=\{1_G\}$;(2) G is
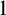 $1$-CLI iff G admits a compatible complete two-sided invariant metric; and
$1$-CLI iff G admits a compatible complete two-sided invariant metric; and(3) G is L-
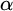 $\alpha $-CLI iff G is locally
$\alpha $-CLI iff G is locally 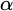 $\alpha $-CLI, i.e., G contains an open subgroup that is
$\alpha $-CLI, i.e., G contains an open subgroup that is 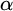 $\alpha $-CLI.
$\alpha $-CLI.
Subsequently, we show this hierarchy is proper by constructing non-archimedean CLI Polish groups 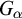 $G_\alpha $ and
$G_\alpha $ and 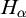 $H_\alpha $ for
$H_\alpha $ for 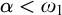 $\alpha <\omega _1$, such that:
$\alpha <\omega _1$, such that:
(1)
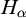 $H_\alpha $ is
$H_\alpha $ is 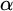 $\alpha $-CLI but not L-
$\alpha $-CLI but not L-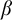 $\beta $-CLI for
$\beta $-CLI for 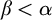 $\beta <\alpha $; and
$\beta <\alpha $; and(2)
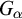 $G_\alpha $ is
$G_\alpha $ is 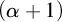 $(\alpha +1)$-CLI but not L-
$(\alpha +1)$-CLI but not L-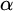 $\alpha $-CLI.
$\alpha $-CLI.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of The Association for Symbolic Logic


