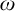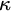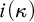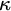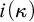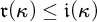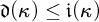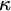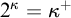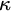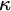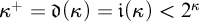1 Introduction
A family
![]() $\mathcal {A}$
contained in
$\mathcal {A}$
contained in
![]() $[\omega ]^{\omega }$
is said to be independent if for every two finite disjoint subfamilies
$[\omega ]^{\omega }$
is said to be independent if for every two finite disjoint subfamilies
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\mathcal {C}$
the set
$\mathcal {C}$
the set
![]() $\bigcap \mathcal {B}\backslash \bigcup \mathcal {C}$
is infinite. We refer to such sets as Boolean combinations. The least size of a maximal (under inclusion) independent family is denoted
$\bigcap \mathcal {B}\backslash \bigcup \mathcal {C}$
is infinite. We refer to such sets as Boolean combinations. The least size of a maximal (under inclusion) independent family is denoted
![]() $\mathfrak {i}$
. For an excellent introduction to the subject of cardinal characteristics of the continuum and definition of various characteristics we refer the reader to [Reference Blass, Foreman and Kanamori2].
$\mathfrak {i}$
. For an excellent introduction to the subject of cardinal characteristics of the continuum and definition of various characteristics we refer the reader to [Reference Blass, Foreman and Kanamori2].
The past decade has seen an increased volume of work regarding natural higher analogues for uncountable cardinals
![]() $\kappa $
of the classical cardinal characteristics. However, even though we already have a comparatively rich literature in this area there is very little known about analogues of the notion of independence. Even in the classical, countable setting, the independence number, and the notion of independence in general, do not seem to be that well-studied. Among the many open questions surrounding independence are the consistency of
$\kappa $
of the classical cardinal characteristics. However, even though we already have a comparatively rich literature in this area there is very little known about analogues of the notion of independence. Even in the classical, countable setting, the independence number, and the notion of independence in general, do not seem to be that well-studied. Among the many open questions surrounding independence are the consistency of
![]() $\text {cof}(\mathfrak {i})=\omega $
and the consistency of
$\text {cof}(\mathfrak {i})=\omega $
and the consistency of
![]() $\mathfrak {i}<\mathfrak {a}$
. A difficulty in the study of the higher independence number is the fact that it is not a priori clear what the natural generalization of the classical independence number should be. Given an uncountable cardinal
$\mathfrak {i}<\mathfrak {a}$
. A difficulty in the study of the higher independence number is the fact that it is not a priori clear what the natural generalization of the classical independence number should be. Given an uncountable cardinal
![]() $\kappa $
Footnote
1
one may consider subfamilies
$\kappa $
Footnote
1
one may consider subfamilies
![]() $\mathcal {A}$
of
$\mathcal {A}$
of
![]() $[\kappa ]^{\kappa }$
which have the property that every Boolean combination generated by strictly less than
$[\kappa ]^{\kappa }$
which have the property that every Boolean combination generated by strictly less than
![]() $\kappa $
many elements of
$\kappa $
many elements of
![]() $\mathcal {A}$
is unbounded. That is, one may require that for every two disjoint subfamilies
$\mathcal {A}$
is unbounded. That is, one may require that for every two disjoint subfamilies
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\mathcal {C}$
of
$\mathcal {C}$
of
![]() $\mathcal {A}$
, such that
$\mathcal {A}$
, such that
![]() $|\mathcal {B}|<\kappa $
and
$|\mathcal {B}|<\kappa $
and
![]() $|\mathcal {C}|<\kappa $
, the Boolean combination
$|\mathcal {C}|<\kappa $
, the Boolean combination
![]() $\bigcap \mathcal {B}\backslash \bigcup \mathcal {C}$
is unbounded. We refer to such families as strongly independent. A major problem presenting itself in the study of this notion of strong independence on
$\bigcap \mathcal {B}\backslash \bigcup \mathcal {C}$
is unbounded. We refer to such families as strongly independent. A major problem presenting itself in the study of this notion of strong independence on
![]() $\kappa $
is the very existence of maximal, under inclusion, strongly independent families. Results regarding these families, together with a number of interesting open questions are included in the last section of the paper. An earlier study of the notion of strong independence can be found in [Reference Kunnen20], where it is shown that the existence of a maximal strongly
$\kappa $
is the very existence of maximal, under inclusion, strongly independent families. Results regarding these families, together with a number of interesting open questions are included in the last section of the paper. An earlier study of the notion of strong independence can be found in [Reference Kunnen20], where it is shown that the existence of a maximal strongly
![]() $\omega _{1}$
-independent family is equiconsistent with the existence of a measurable.
$\omega _{1}$
-independent family is equiconsistent with the existence of a measurable.
A more restrictive, but fruitful, approach towards the generalization of the classical notion of independence is the requirement that for a given family
![]() $\mathcal {A}\subseteq [\kappa ]^{\kappa }$
the finitely generated Boolean combinations are unbounded. That is, given a family
$\mathcal {A}\subseteq [\kappa ]^{\kappa }$
the finitely generated Boolean combinations are unbounded. That is, given a family
![]() $\mathcal {A}\subseteq [\kappa ]^{\kappa }$
we say that
$\mathcal {A}\subseteq [\kappa ]^{\kappa }$
we say that
![]() $\mathcal {A}$
is
$\mathcal {A}$
is
![]() $\kappa $
-independent if for every two disjoint finite subfamilies
$\kappa $
-independent if for every two disjoint finite subfamilies
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\mathcal {C}$
contained in
$\mathcal {C}$
contained in
![]() $\mathcal {A}$
, the set
$\mathcal {A}$
, the set
![]() $\bigcap \mathcal {B}\backslash \bigcup \mathcal {C}$
is unbounded.Footnote
2
The existence of a maximal under inclusion
$\bigcap \mathcal {B}\backslash \bigcup \mathcal {C}$
is unbounded.Footnote
2
The existence of a maximal under inclusion
![]() $\kappa $
-independent family is provided by the Axiom of Choice and thus given an uncountable regular cardinal
$\kappa $
-independent family is provided by the Axiom of Choice and thus given an uncountable regular cardinal
![]() $\kappa $
, one can define the higher independence number, denoted
$\kappa $
, one can define the higher independence number, denoted
![]() $\mathfrak {i}(\kappa )$
, to be the minimal size of a maximal
$\mathfrak {i}(\kappa )$
, to be the minimal size of a maximal
![]() $\kappa $
-independent family. A standard diagonalization argument going over all Boolean combinations, shows that
$\kappa $
-independent family. A standard diagonalization argument going over all Boolean combinations, shows that
![]() $\kappa ^{+}\leq \mathfrak {i}(\kappa )$
. Classical examples of independent families of cardinality
$\kappa ^{+}\leq \mathfrak {i}(\kappa )$
. Classical examples of independent families of cardinality
![]() $2^{\omega }$
do generalize into the uncountable and provide the existence of
$2^{\omega }$
do generalize into the uncountable and provide the existence of
![]() $\kappa $
-independent families and so of maximal
$\kappa $
-independent families and so of maximal
![]() $\kappa $
-independent families of cardinality
$\kappa $
-independent families of cardinality
![]() $2^{\kappa }$
(see Lemma 2.4). An example of a strongly
$2^{\kappa }$
(see Lemma 2.4). An example of a strongly
![]() $\kappa $
-independent family of cardinality
$\kappa $
-independent family of cardinality
![]() $2^{\kappa }$
, under some additional hypothesis on
$2^{\kappa }$
, under some additional hypothesis on
![]() $\kappa $
, is provided in Lemma 10.2.
$\kappa $
, is provided in Lemma 10.2.
One of the main breakthroughs in the study of the classical independence number is the consistency of
![]() $\mathfrak {i}<\mathfrak {u}$
, established in 1992 by Shelah (see [Reference Shelah22]). The consistency proof carries a somewhat hidden construction of a Sacks indestructible maximal independent family, that is a maximal independent family which remains maximal after the countable support product and countable support iterations of Sacks forcing. A tree version of Shelah’s poset, known as party forcing, has been used in [Reference Chodounsky, Grebik and Fischer7] to establish the consistency of
$\mathfrak {i}<\mathfrak {u}$
, established in 1992 by Shelah (see [Reference Shelah22]). The consistency proof carries a somewhat hidden construction of a Sacks indestructible maximal independent family, that is a maximal independent family which remains maximal after the countable support product and countable support iterations of Sacks forcing. A tree version of Shelah’s poset, known as party forcing, has been used in [Reference Chodounsky, Grebik and Fischer7] to establish the consistency of
![]() $\mathfrak {i}=\mathfrak {f}<\mathfrak {u}$
, where
$\mathfrak {i}=\mathfrak {f}<\mathfrak {u}$
, where
![]() $\mathfrak {f}$
is the free sequences number.Footnote
3
For recent studies on Sacks indestructible, co-analytic maximal independent families see [Reference Brendle, Fischer and Khomskii5], as well as [Reference Bergfalk, Fischer and Switzer1, Reference Cruz-Chapital, Fischer, Guzman and Supina9, Reference Switzer23]. In this paper, we prove:
$\mathfrak {f}$
is the free sequences number.Footnote
3
For recent studies on Sacks indestructible, co-analytic maximal independent families see [Reference Brendle, Fischer and Khomskii5], as well as [Reference Bergfalk, Fischer and Switzer1, Reference Cruz-Chapital, Fischer, Guzman and Supina9, Reference Switzer23]. In this paper, we prove:
Theorem. Let
![]() $\kappa $
be a measurable cardinal and let
$\kappa $
be a measurable cardinal and let
![]() $2^{\kappa }=\kappa ^{+}$
. Then there is a maximal
$2^{\kappa }=\kappa ^{+}$
. Then there is a maximal
![]() $\kappa $
-independent family which remains maximal after the
$\kappa $
-independent family which remains maximal after the
![]() $\kappa $
-support product of
$\kappa $
-support product of
![]() $\lambda $
-many copies of
$\lambda $
-many copies of
![]() $\kappa $
-Sacks forcing.
$\kappa $
-Sacks forcing.
The existence of this indestructible maximal
![]() $\kappa $
-independent family is closely related to the properties of a normal measure
$\kappa $
-independent family is closely related to the properties of a normal measure
![]() $\mathcal {U}$
on
$\mathcal {U}$
on
![]() $\kappa $
. With the indestructible family
$\kappa $
. With the indestructible family
![]() $\mathcal {A}$
, we associate a
$\mathcal {A}$
, we associate a
![]() $\kappa ^{+}$
-complete filter
$\kappa ^{+}$
-complete filter
![]() $\operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
which is properly contained in
$\operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
which is properly contained in
![]() $\mathcal {U}$
and its elements meet every Boolean combination on an unbounded set. The properties of this filter capture to a great extent the indestructibility of the associated independent family.
$\mathcal {U}$
and its elements meet every Boolean combination on an unbounded set. The properties of this filter capture to a great extent the indestructibility of the associated independent family.
For readers familiar with the countable setting, we will draw a more detailed comparison. As developed originally in the work of Shelah [Reference Shelah22] and later analyzed for example in [Reference Chodounsky, Grebik and Fischer7], an independent family which is maximal in a strong sense and whose density filter (a similarly to
![]() $\operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
associated filter) is selective (which means both a P-set and Q-set) is indestructible by countable support products and iterations of Sacks forcing. While
$\operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
associated filter) is selective (which means both a P-set and Q-set) is indestructible by countable support products and iterations of Sacks forcing. While
![]() $\operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
is a
$\operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
is a
![]() $\kappa $
-P-set, in the sense that every subfamily of cardinality
$\kappa $
-P-set, in the sense that every subfamily of cardinality
![]() $\leq \kappa $
has a pseudo-intersection in the filter (see Definition 5.4 and Lemma 5.5), the role of the Q-set property from the countable setting is taken by the fact that for every ground model strictly increasing function in
$\leq \kappa $
has a pseudo-intersection in the filter (see Definition 5.4 and Lemma 5.5), the role of the Q-set property from the countable setting is taken by the fact that for every ground model strictly increasing function in
![]() $^{\kappa }\kappa $
there is a set in the filter whose enumeration function grows faster than the given function (see Lemma 5.6 and Corollary 5.7).Footnote
4
In both, the countable and the uncountable setting a strengthening of the maximality of the corresponding maximal independent family plays an important role. In the countable setting this strengthening is known as dense maximality, a property which originally appears in [Reference Goldstern and Shelah16]. The
$^{\kappa }\kappa $
there is a set in the filter whose enumeration function grows faster than the given function (see Lemma 5.6 and Corollary 5.7).Footnote
4
In both, the countable and the uncountable setting a strengthening of the maximality of the corresponding maximal independent family plays an important role. In the countable setting this strengthening is known as dense maximality, a property which originally appears in [Reference Goldstern and Shelah16]. The
![]() $\kappa $
-maximal independent family which we construct is densely maximal in a similar sense (see Definition 6.1). Moreover we make an explicit use of an equivalent characterisation of dense maximality given in Lemma 6.2, characterization which plays a key role in our main theorem. An analogue to the countable setting of the overall approach, which we take in this paper can be found in the more recent studies [Reference Bergfalk, Fischer and Switzer1, Reference Cruz-Chapital, Fischer, Guzman and Supina9, Reference Switzer23]. Note that an analogue of the equivalent characterization given in Lemma 6.2 implicitly appears in [Reference Shelah22].
$\kappa $
-maximal independent family which we construct is densely maximal in a similar sense (see Definition 6.1). Moreover we make an explicit use of an equivalent characterisation of dense maximality given in Lemma 6.2, characterization which plays a key role in our main theorem. An analogue to the countable setting of the overall approach, which we take in this paper can be found in the more recent studies [Reference Bergfalk, Fischer and Switzer1, Reference Cruz-Chapital, Fischer, Guzman and Supina9, Reference Switzer23]. Note that an analogue of the equivalent characterization given in Lemma 6.2 implicitly appears in [Reference Shelah22].
Finally, the existence of a
![]() $\kappa $
-mad family, which remains maximal after an arbitrarily long
$\kappa $
-mad family, which remains maximal after an arbitrarily long
![]() $\kappa $
-supported product of
$\kappa $
-supported product of
![]() $\kappa $
-Sacks reals is a straightforward generalization of the classical case. Moreover, if
$\kappa $
-Sacks reals is a straightforward generalization of the classical case. Moreover, if
![]() $\mathfrak {d}(\kappa )=\kappa ^{+}$
then
$\mathfrak {d}(\kappa )=\kappa ^{+}$
then
![]() $\mathfrak {a}(\kappa )=\kappa ^{+}$
(see [Reference Blass, Hyttinen and Zhang3, Reference Raghavan and Shelah21]). Thus our result leads to the following statement:
$\mathfrak {a}(\kappa )=\kappa ^{+}$
(see [Reference Blass, Hyttinen and Zhang3, Reference Raghavan and Shelah21]). Thus our result leads to the following statement:
Theorem. Let
![]() $\kappa $
be a measurable cardinal and
$\kappa $
be a measurable cardinal and
![]() $2^{\kappa }=\kappa ^{+}$
. Then there is a cardinal preserving generic extension in which
$2^{\kappa }=\kappa ^{+}$
. Then there is a cardinal preserving generic extension in which
One of the very interesting open questions regarding the classical independence number is the consistency of
![]() $\mathfrak {i}<\mathfrak {a}$
. As a very partial result towards this question we obtain the following:
$\mathfrak {i}<\mathfrak {a}$
. As a very partial result towards this question we obtain the following:
Corollary. Let
![]() $\kappa $
be regular uncountable. If
$\kappa $
be regular uncountable. If
![]() $\mathfrak {i}(\kappa )=\kappa ^{+}$
then
$\mathfrak {i}(\kappa )=\kappa ^{+}$
then
![]() $\mathfrak {a}(\kappa )=\kappa ^{+}$
.
$\mathfrak {a}(\kappa )=\kappa ^{+}$
.
1.1 Structure of the paper
In Section 2 we define a notion of independence at
![]() $\kappa $
, for
$\kappa $
, for
![]() $\kappa $
arbitrary infinite cardinal and define the cardinal number
$\kappa $
arbitrary infinite cardinal and define the cardinal number
![]() $\mathfrak {i}(\kappa )$
for
$\mathfrak {i}(\kappa )$
for
![]() $\kappa $
regular uncountable. In Section 3, given a measurable cardinal
$\kappa $
regular uncountable. In Section 3, given a measurable cardinal
![]() $\kappa $
, witnessed by a normal measure
$\kappa $
, witnessed by a normal measure
![]() $\mathcal {U}$
and working under the hypothesis that
$\mathcal {U}$
and working under the hypothesis that
![]() $2^{\kappa }=\kappa ^{+}$
, we define a
$2^{\kappa }=\kappa ^{+}$
, we define a
![]() $\kappa ^{+}$
closed poset
$\kappa ^{+}$
closed poset
![]() $\mathbb {P}_{\mathcal {U}}$
which adjoins a maximal
$\mathbb {P}_{\mathcal {U}}$
which adjoins a maximal
![]() $\kappa $
-independent family, which we denote
$\kappa $
-independent family, which we denote
![]() $\mathcal {A}_{G}$
.Footnote
5
In Section 4 we study the properties of an ideal on
$\mathcal {A}_{G}$
.Footnote
5
In Section 4 we study the properties of an ideal on
![]() $\kappa $
, to which we refer as density ideal and denote
$\kappa $
, to which we refer as density ideal and denote
![]() $\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
, which is contained in the dual ideal of
$\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
, which is contained in the dual ideal of
![]() $\mathcal {U}$
and which naturally captures crucial properties of the independent family
$\mathcal {U}$
and which naturally captures crucial properties of the independent family
![]() $\mathcal {A}_{G}$
. In Section 5.1, we show that the dual filter of this ideal, denoted
$\mathcal {A}_{G}$
. In Section 5.1, we show that the dual filter of this ideal, denoted
![]() $\operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
is a
$\operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
is a
![]() $\kappa $
-P-set. In Section 6 we show that the family
$\kappa $
-P-set. In Section 6 we show that the family
![]() $\mathcal {A}_{G}$
is densely maximal in a natural sense and characterize dense maximality in terms of properties of the density ideal. Section 7 introduces the concepts of preprocessed conditions and outer hulls necessary for the proofs in the last section. In Section 8 we prove our main theorem, by showing that the densely maximal
$\mathcal {A}_{G}$
is densely maximal in a natural sense and characterize dense maximality in terms of properties of the density ideal. Section 7 introduces the concepts of preprocessed conditions and outer hulls necessary for the proofs in the last section. In Section 8 we prove our main theorem, by showing that the densely maximal
![]() $\kappa $
-independent family
$\kappa $
-independent family
![]() $\mathcal {A}_{G}$
remains maximal after the
$\mathcal {A}_{G}$
remains maximal after the
![]() $\kappa $
-support product of
$\kappa $
-support product of
![]() $\lambda $
many copies of
$\lambda $
many copies of
![]() $\kappa $
-Sacks forcing. We conclude the paper with some open questions and an appendix, discussing the notion of strong independence.
$\kappa $
-Sacks forcing. We conclude the paper with some open questions and an appendix, discussing the notion of strong independence.
2 The higher independence number
In the following we set to define a higher analogue of the notion of independent families on
![]() $\omega $
for the special case in which the Boolean combinations are finitely generated.
$\omega $
for the special case in which the Boolean combinations are finitely generated.
Definition 2.1. Let
![]() $\kappa $
be a regular uncountable cardinal and let
$\kappa $
be a regular uncountable cardinal and let
![]() $\operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
be the set of all finite partial functions with domain included in
$\operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
be the set of all finite partial functions with domain included in
![]() $\mathcal {A}$
and range the set
$\mathcal {A}$
and range the set
![]() $\{0,1\}$
. For each
$\{0,1\}$
. For each
![]() $h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
let
$h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
let
![]() $\mathcal {A}^{h}=\bigcap \{\mathcal {A}^{h(A)}:A\in \operatorname {\mathrm {dom}}(h)\}$
where
$\mathcal {A}^{h}=\bigcap \{\mathcal {A}^{h(A)}:A\in \operatorname {\mathrm {dom}}(h)\}$
where
![]() $\mathcal {A}^{h(A)}=A$
if
$\mathcal {A}^{h(A)}=A$
if
![]() $h(A)=0$
and
$h(A)=0$
and
![]() $\mathcal {A}^{h(A)}=\kappa \backslash A$
if
$\mathcal {A}^{h(A)}=\kappa \backslash A$
if
![]() $h(A)=1$
. We refer to sets of the form
$h(A)=1$
. We refer to sets of the form
![]() $\mathcal {A}^{h}$
as Boolean combinations.
$\mathcal {A}^{h}$
as Boolean combinations.
With this we can state the definition of
![]() $\kappa $
-independence. For a discussion of the most general definition in which the Boolean combinations are generated by arbitrarily large subfamilies of the given family, see [Reference Fischer and Eskew10].
$\kappa $
-independence. For a discussion of the most general definition in which the Boolean combinations are generated by arbitrarily large subfamilies of the given family, see [Reference Fischer and Eskew10].
Definition 2.2.
-
(1) A family
 $\mathcal {A}\subseteq [\kappa ]^{\kappa }$
is said to be
$\mathcal {A}\subseteq [\kappa ]^{\kappa }$
is said to be
 $\kappa $
-independent if for each
$\kappa $
-independent if for each
 $h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
the set
$h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
the set
 $\mathcal {A}^{h}$
is unbounded. It is said to be a maximal
$\mathcal {A}^{h}$
is unbounded. It is said to be a maximal
 $\kappa $
-independent family if it is
$\kappa $
-independent family if it is
 $\kappa $
-independent and maximal under inclusion.
$\kappa $
-independent and maximal under inclusion. -
(2) The least size of a maximal
 $\kappa $
-independent family is denoted
$\kappa $
-independent family is denoted
 $\mathfrak {i}(\kappa )$
.
$\mathfrak {i}(\kappa )$
.
Remark 2.3. For
![]() $\kappa =\omega $
the above notions coincide with the classical notions of independence on
$\kappa =\omega $
the above notions coincide with the classical notions of independence on
![]() $[\omega ]^{\omega }$
and
$[\omega ]^{\omega }$
and
![]() $\mathfrak {i}(\kappa )=\mathfrak {i}$
, where
$\mathfrak {i}(\kappa )=\mathfrak {i}$
, where
![]() $\mathfrak {i}$
is the classical independence number.
$\mathfrak {i}$
is the classical independence number.
Lemma 2.4. Let
![]() $\kappa $
be a regular infinite cardinal. Then
$\kappa $
be a regular infinite cardinal. Then
-
(1) Every
 $\kappa $
-independent family is contained in a maximal
$\kappa $
-independent family is contained in a maximal
 $\kappa $
-independent family.
$\kappa $
-independent family. -
(2)
 $\kappa ^{+}\leq \mathfrak {r}(\kappa )\leq \mathfrak {i}(\kappa )$
.
$\kappa ^{+}\leq \mathfrak {r}(\kappa )\leq \mathfrak {i}(\kappa )$
. -
(3) There is a maximal
 $\kappa $
-independent family of cardinality
$\kappa $
-independent family of cardinality
 $2^{\kappa }$
.
$2^{\kappa }$
. -
(4)
 $\mathfrak {d}(\kappa )\leq \mathfrak {i}(\kappa )$
.
$\mathfrak {d}(\kappa )\leq \mathfrak {i}(\kappa )$
.
Proof Since the increasing union of a collection of
![]() $\kappa $
-independent families is
$\kappa $
-independent families is
![]() $\kappa $
-independent, by the Axiom of Choice every
$\kappa $
-independent, by the Axiom of Choice every
![]() $\kappa $
-independent family is contained in a maximal one. Note that if
$\kappa $
-independent family is contained in a maximal one. Note that if
![]() $\mathcal {A}$
is a maximal
$\mathcal {A}$
is a maximal
![]() $\kappa $
-independent family, then the set of Boolean combinations
$\kappa $
-independent family, then the set of Boolean combinations
![]() $\{\mathcal {A}^{h}: h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})\}$
is not split and so
$\{\mathcal {A}^{h}: h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})\}$
is not split and so
![]() $\mathfrak {r}(\kappa )\leq |\mathcal {A}|$
. For a construction of a
$\mathfrak {r}(\kappa )\leq |\mathcal {A}|$
. For a construction of a
![]() $\kappa $
-independent family of cardinality
$\kappa $
-independent family of cardinality
![]() $2^{\kappa }$
, see [Reference Geschke14, Theorem 4.2]. Finally, the proof that
$2^{\kappa }$
, see [Reference Geschke14, Theorem 4.2]. Finally, the proof that
![]() $\mathfrak {d}(\kappa )\leq \mathfrak {i}(\kappa )$
follows closely the proof of the classical case, i.e.,
$\mathfrak {d}(\kappa )\leq \mathfrak {i}(\kappa )$
follows closely the proof of the classical case, i.e.,
![]() $\mathfrak {d}\leq \mathfrak {i}$
(see [Reference Halbeisen18]).
$\mathfrak {d}\leq \mathfrak {i}$
(see [Reference Halbeisen18]).
One of the most interesting open questions, regarding the classical cardinal characteristics is the consistency of
![]() $\mathfrak {i}<\mathfrak {a}$
. By the last item of the above theorem and the fact that if
$\mathfrak {i}<\mathfrak {a}$
. By the last item of the above theorem and the fact that if
![]() $\mathfrak {d}(\kappa )=\kappa ^{+}$
implies that
$\mathfrak {d}(\kappa )=\kappa ^{+}$
implies that
![]() $\mathfrak {a}(\kappa )=\kappa ^{+}$
(see [Reference Blass, Hyttinen and Zhang3, Reference Raghavan and Shelah21]), we obtain the following:
$\mathfrak {a}(\kappa )=\kappa ^{+}$
(see [Reference Blass, Hyttinen and Zhang3, Reference Raghavan and Shelah21]), we obtain the following:
Corollary 2.5. Let
![]() $\kappa $
be a regular uncountable cardinal. Then if
$\kappa $
be a regular uncountable cardinal. Then if
![]() $\mathfrak {i}(\kappa )=\kappa ^{+}$
then
$\mathfrak {i}(\kappa )=\kappa ^{+}$
then
![]() $\mathfrak {a}(\kappa )=\kappa ^{+}$
.
$\mathfrak {a}(\kappa )=\kappa ^{+}$
.
3 Adjoining a maximal
 $\kappa $
-independent family
$\kappa $
-independent family
In this section, we provide a partial order which adjoins a maximal
![]() $\kappa $
-independent family, a family which we will later show to be indestructible by products of
$\kappa $
-independent family, a family which we will later show to be indestructible by products of
![]() $\kappa $
-Sacks forcing.
$\kappa $
-Sacks forcing.
Let
![]() $\kappa $
be a measurable cardinal and
$\kappa $
be a measurable cardinal and
![]() $\mathcal {U}$
a normal measure on
$\mathcal {U}$
a normal measure on
![]() $\kappa $
.
$\kappa $
.
Definition 3.1. Let
![]() $\mathbb {P}_{\mathcal {U}}$
be the poset of all pairs
$\mathbb {P}_{\mathcal {U}}$
be the poset of all pairs
![]() $(\mathcal {A},A)$
where
$(\mathcal {A},A)$
where
![]() $\mathcal {A}$
is a
$\mathcal {A}$
is a
![]() $\kappa $
-independent family of cardinality
$\kappa $
-independent family of cardinality
![]() $\kappa $
and
$\kappa $
and
![]() $A\in \mathcal {U}$
has the property that
$A\in \mathcal {U}$
has the property that
![]() $\forall h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
the set
$\forall h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
the set
![]() $\mathcal {A}^{h}\cap A$
is unbounded. The extension relation is defined as follows:
$\mathcal {A}^{h}\cap A$
is unbounded. The extension relation is defined as follows:
![]() $(\mathcal {A}_{1},A_{1})\leq (\mathcal {A}_{0},A_{0})$
if and only if
$(\mathcal {A}_{1},A_{1})\leq (\mathcal {A}_{0},A_{0})$
if and only if
![]() $\mathcal {A}_{1}\supseteq \mathcal {A}_{0}$
and
$\mathcal {A}_{1}\supseteq \mathcal {A}_{0}$
and
![]() $A_{1}\subseteq ^{*} A_{0}$
.Footnote
6
$A_{1}\subseteq ^{*} A_{0}$
.Footnote
6
Lemma 3.2. Assume
![]() $2^{\kappa }=\kappa ^{+}$
. Then
$2^{\kappa }=\kappa ^{+}$
. Then
![]() $\mathbb {P}_{\mathcal {U}}$
is
$\mathbb {P}_{\mathcal {U}}$
is
![]() $\kappa ^{+}$
-closed and
$\kappa ^{+}$
-closed and
![]() $\kappa ^{++}\mathrm{{-}cc}$
.
$\kappa ^{++}\mathrm{{-}cc}$
.
Proof. Let
![]() $\{(\mathcal {A}_{i},A_{i})\}_{i\in \kappa }$
be a decreasing sequence in
$\{(\mathcal {A}_{i},A_{i})\}_{i\in \kappa }$
be a decreasing sequence in
![]() $\mathbb {P}_{\mathcal {U}}$
. We can assume that
$\mathbb {P}_{\mathcal {U}}$
. We can assume that
![]() $\{A_{i}\}_{i\in \kappa }$
is strictly decreasing, i.e., for each
$\{A_{i}\}_{i\in \kappa }$
is strictly decreasing, i.e., for each
![]() $i>j$
we have
$i>j$
we have
![]() $A_{j}\subseteq A_{i}$
. Then
$A_{j}\subseteq A_{i}$
. Then
![]() $\mathcal {A}=\bigcup _{i\in \kappa }\mathcal {A}_{i}$
is an independent family of cardinality
$\mathcal {A}=\bigcup _{i\in \kappa }\mathcal {A}_{i}$
is an independent family of cardinality
![]() $\kappa $
and the diagonal intersection
$\kappa $
and the diagonal intersection
![]() $A^{\prime }=\Delta _{i\in \kappa }A_{i}\in \mathcal {U}$
.
$A^{\prime }=\Delta _{i\in \kappa }A_{i}\in \mathcal {U}$
.
Now, for each
![]() $i\in \kappa $
, let
$i\in \kappa $
, let
![]() $\{h_{i,j}\}_{j\in \kappa }$
enumerate
$\{h_{i,j}\}_{j\in \kappa }$
enumerate
![]() $\operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
. Recursively we will define a set
$\operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
. Recursively we will define a set
![]() $A^{\prime \prime }=\{k_{i,l,m}\}_{l,m<i; i<\kappa }$
which is a pseudo-intersection of
$A^{\prime \prime }=\{k_{i,l,m}\}_{l,m<i; i<\kappa }$
which is a pseudo-intersection of
![]() $\{A_{i}\}_{i\in \kappa }$
and which meets every Boolean combination
$\{A_{i}\}_{i\in \kappa }$
and which meets every Boolean combination
![]() $\mathcal {A}^{h}$
for
$\mathcal {A}^{h}$
for
![]() $h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
on an unbounded set. Then
$h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
on an unbounded set. Then
![]() $A=A^{\prime }\cup A^{\prime \prime }$
is an element of
$A=A^{\prime }\cup A^{\prime \prime }$
is an element of
![]() $\mathcal {U}$
and
$\mathcal {U}$
and
![]() $(\mathcal {A},A)\in \mathbb {P}_{\mathcal {U}}$
is a common extension of
$(\mathcal {A},A)\in \mathbb {P}_{\mathcal {U}}$
is a common extension of
![]() $\{(\mathcal {A}_{i},A_{i})\}_{i\in \kappa }$
.
$\{(\mathcal {A}_{i},A_{i})\}_{i\in \kappa }$
.
3.1 Construction of
 $A^{\prime \prime }$
$A^{\prime \prime }$
At step i pick
![]() $k_{i,m,l}\in A_{i}\cap \mathcal {A}_{i}^{h_{m,l}}$
for each
$k_{i,m,l}\in A_{i}\cap \mathcal {A}_{i}^{h_{m,l}}$
for each
![]() $m,l<i$
. Then in particular
$m,l<i$
. Then in particular
![]() $k_{i,m,l}\in A_{m}$
for each
$k_{i,m,l}\in A_{m}$
for each
![]() $m\leq i$
and
$m\leq i$
and
![]() $k_{i,m,l}\in \mathcal {A}_{m}^{h_{m,l}}$
for each
$k_{i,m,l}\in \mathcal {A}_{m}^{h_{m,l}}$
for each
![]() $m,l < i$
. Take
$m,l < i$
. Take
![]() $A^{\prime \prime }=\{k_{i,m,l}\}_{m,l<i;i<\kappa }$
. Then
$A^{\prime \prime }=\{k_{i,m,l}\}_{m,l<i;i<\kappa }$
. Then
![]() $A^{\prime \prime }$
meets every Boolean combination on an unbounded set and is a pseudo-intersection. Fix
$A^{\prime \prime }$
meets every Boolean combination on an unbounded set and is a pseudo-intersection. Fix
![]() $\gamma \in \kappa $
. Then for all
$\gamma \in \kappa $
. Then for all
![]() $\xi $
such that
$\xi $
such that
![]() $\xi>\gamma $
and all
$\xi>\gamma $
and all
![]() $m,l<\xi $
we have that
$m,l<\xi $
we have that
![]() $k_{\xi ,l,m}\in A_{\xi }\subseteq A_{\gamma }$
. Thus
$k_{\xi ,l,m}\in A_{\xi }\subseteq A_{\gamma }$
. Thus
![]() $A^{\prime \prime }\backslash A_{\gamma }\subseteq \{k_{\xi ,l,m}\}_{\xi <\gamma; l,m<\xi }$
, which is a bounded set.
$A^{\prime \prime }\backslash A_{\gamma }\subseteq \{k_{\xi ,l,m}\}_{\xi <\gamma; l,m<\xi }$
, which is a bounded set.
The poset has the
![]() $\kappa ^{++}$
-cc, because
$\kappa ^{++}$
-cc, because
![]() $|\mathbb {P}_{\mathcal {U}}|=\kappa ^{+}$
. Indeed,
$|\mathbb {P}_{\mathcal {U}}|=\kappa ^{+}$
. Indeed,
![]() $\Big |\big [[\kappa ]^{\kappa }\big ]^{\kappa }\Big |=\kappa ^{+}$
.⊣
$\Big |\big [[\kappa ]^{\kappa }\big ]^{\kappa }\Big |=\kappa ^{+}$
.⊣
Lemma 3.3. If
![]() $(\mathcal {A},A)\in \mathbb {P}_{\mathcal {U}}$
, then there is
$(\mathcal {A},A)\in \mathbb {P}_{\mathcal {U}}$
, then there is
![]() $B\notin \mathcal {A}$
such that
$B\notin \mathcal {A}$
such that
![]() $B\subseteq A$
and
$B\subseteq A$
and
![]() $(\mathcal {A}\cup \{B\},A)\leq (\mathcal {A},A)$
.
$(\mathcal {A}\cup \{B\},A)\leq (\mathcal {A},A)$
.
Proof Let
![]() $\{h_{i}\}_{i\in \kappa }$
be a fixed enumeration of
$\{h_{i}\}_{i\in \kappa }$
be a fixed enumeration of
![]() $\operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
. Since
$\operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
. Since
![]() $\mathcal {A}^{h_{0}}\cap A$
is unbounded, we can find distinct
$\mathcal {A}^{h_{0}}\cap A$
is unbounded, we can find distinct
![]() $k_{0,0}$
,
$k_{0,0}$
,
![]() $k_{0,1}$
in
$k_{0,1}$
in
![]() $\mathcal {A}^{h_{0}}\cap A$
. Suppose we have defined
$\mathcal {A}^{h_{0}}\cap A$
. Suppose we have defined
![]() $\{k_{i,j}: i\in \gamma , j\in 2\}$
distinct. Since
$\{k_{i,j}: i\in \gamma , j\in 2\}$
distinct. Since
![]() $\mathcal {A}^{h_{\gamma }}\cap A$
is unbounded, we can find distinct
$\mathcal {A}^{h_{\gamma }}\cap A$
is unbounded, we can find distinct
![]() $k_{\gamma ,0}, k_{\gamma ,1}$
in
$k_{\gamma ,0}, k_{\gamma ,1}$
in
![]() $(\mathcal {A}^{h_{\gamma }}\cap A)\backslash \{k_{i,j}: i\in \gamma , j\in 2\}$
. Finally, take
$(\mathcal {A}^{h_{\gamma }}\cap A)\backslash \{k_{i,j}: i\in \gamma , j\in 2\}$
. Finally, take
![]() $B=\{k_{i,0}\}_{i\in \kappa }$
. Clearly
$B=\{k_{i,0}\}_{i\in \kappa }$
. Clearly
![]() $B\subseteq A$
and
$B\subseteq A$
and
![]() $\mathcal {A}\cup \{B\}$
is independent. To verify the latter note that for each
$\mathcal {A}\cup \{B\}$
is independent. To verify the latter note that for each
![]() $h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
there are unboundedly many
$h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
there are unboundedly many
![]() $h_{i}\supseteq h$
. Then for unboundedly many
$h_{i}\supseteq h$
. Then for unboundedly many
![]() $i\in \kappa $
,
$i\in \kappa $
,
![]() $k_{i,0}\in \mathcal {A}^{h_{i}}\cap B\subseteq \mathcal {A}^{h}\cap B$
and
$k_{i,0}\in \mathcal {A}^{h_{i}}\cap B\subseteq \mathcal {A}^{h}\cap B$
and
![]() $k_{i,1}\in \mathcal {A}^{h_{i}}\backslash B\subseteq \mathcal {A}^{h}\backslash B$
.
$k_{i,1}\in \mathcal {A}^{h_{i}}\backslash B\subseteq \mathcal {A}^{h}\backslash B$
.
Corollary 3.4. Let G be
![]() $\mathbb {P}_{\mathcal {U}}$
-generic filter. Then
$\mathbb {P}_{\mathcal {U}}$
-generic filter. Then
![]() $\mathcal {A}_{G}=\bigcup \{\mathcal {A}: \exists A\in \mathcal {U} \text { with }(\mathcal {A},A)\in G\}$
is a
$\mathcal {A}_{G}=\bigcup \{\mathcal {A}: \exists A\in \mathcal {U} \text { with }(\mathcal {A},A)\in G\}$
is a
![]() $\kappa $
-maximal independent family.
$\kappa $
-maximal independent family.
Proof Suppose
![]() $X\in [\kappa ]^{\kappa }\setminus \mathcal {A}_{G}$
and
$X\in [\kappa ]^{\kappa }\setminus \mathcal {A}_{G}$
and
![]() $\mathcal {A}_{G}\cup \{X\}$
is independent. Take
$\mathcal {A}_{G}\cup \{X\}$
is independent. Take
![]() $(\mathcal {A},A)\in G$
such that
$(\mathcal {A},A)\in G$
such that
Since
![]() $\mathbb {P}_{\mathcal {U}}$
is
$\mathbb {P}_{\mathcal {U}}$
is
![]() $\kappa ^{+}$
-closed, the set X belongs to the ground model. Now, if for each
$\kappa ^{+}$
-closed, the set X belongs to the ground model. Now, if for each
![]() $h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
the intersections
$h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
the intersections
![]() $\mathcal {A}^{h}\cap X\cap A$
and
$\mathcal {A}^{h}\cap X\cap A$
and
![]() $\mathcal {A}^{h}\cap A\cap X^{c}$
are unbounded, then
$\mathcal {A}^{h}\cap A\cap X^{c}$
are unbounded, then
![]() $(\mathcal {A}\cup \{X\},A)\leq (\mathcal {A},A)$
and
$(\mathcal {A}\cup \{X\},A)\leq (\mathcal {A},A)$
and
which is a contradiction. Therefore there is
![]() $h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
such that either
$h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
such that either
![]() $\mathcal {A}^{h}\cap A\cap X$
or
$\mathcal {A}^{h}\cap A\cap X$
or
![]() $\mathcal {A}^{h}\cap A\cap X^{c}$
is bounded. However, by Lemma 3.3, there is
$\mathcal {A}^{h}\cap A\cap X^{c}$
is bounded. However, by Lemma 3.3, there is
![]() $B\notin \mathcal {A}$
such that
$B\notin \mathcal {A}$
such that
![]() $B\subseteq A$
and
$B\subseteq A$
and
![]() $(\mathcal {A}\cup \{B\},A)\leq (\mathcal {A},A)$
. But then,
$(\mathcal {A}\cup \{B\},A)\leq (\mathcal {A},A)$
. But then,
Therefore
![]() $(\mathcal {A}\cup \{B\}, A)\Vdash "\mathcal {A}_{G}\cup \{X\}\text { is not independent},\text{"}$
which is a contradiction.
$(\mathcal {A}\cup \{B\}, A)\Vdash "\mathcal {A}_{G}\cup \{X\}\text { is not independent},\text{"}$
which is a contradiction.
Remark 3.5. Given a measurable cardinal
![]() $\kappa $
and a normal measure
$\kappa $
and a normal measure
![]() $\mathcal {U}$
on
$\mathcal {U}$
on
![]() $\kappa $
, whenever
$\kappa $
, whenever
![]() $\mathcal {A}=\mathcal {A}_{G}$
is the generic maximal
$\mathcal {A}=\mathcal {A}_{G}$
is the generic maximal
![]() $\kappa $
-independent family given by a
$\kappa $
-independent family given by a
![]() $\mathbb {P}_{\mathcal {U}}$
-generic filter G, we will say that
$\mathbb {P}_{\mathcal {U}}$
-generic filter G, we will say that
![]() $\mathcal {A}$
is
$\mathcal {A}$
is
![]() $\mathcal {U}$
-supported.
$\mathcal {U}$
-supported.
4 The density ideal
The density ideal (see [Reference Fischer and Montoya11]) plays an important role in describing the properties of maximal independent families on
![]() $\omega $
. A higher analogue of this notion will play an equally important role in the study of maximal
$\omega $
. A higher analogue of this notion will play an equally important role in the study of maximal
![]() $\kappa $
-independent families indestructible by
$\kappa $
-independent families indestructible by
![]() $\kappa $
-Sacks forcing.
$\kappa $
-Sacks forcing.
Definition 4.1. Let
![]() $\mathcal {A}$
be a
$\mathcal {A}$
be a
![]() $\mathcal {U}$
-supported independent family. The density ideal
$\mathcal {U}$
-supported independent family. The density ideal
![]() $\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
is the ideal of all
$\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
is the ideal of all
![]() $X\in \mathcal {U}^{*}$
, where
$X\in \mathcal {U}^{*}$
, where
![]() $\mathcal {U}^{*}$
is the dual ideal of
$\mathcal {U}^{*}$
is the dual ideal of
![]() $\mathcal {U}$
, such that
$\mathcal {U}$
, such that
![]() $\forall h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
there is
$\forall h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
there is
![]() $h^{\prime }\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
such that
$h^{\prime }\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
such that
![]() $h^{\prime }\supseteq h$
and
$h^{\prime }\supseteq h$
and
![]() $\mathcal {A}^{h^{\prime }}\cap X=\emptyset $
.
$\mathcal {A}^{h^{\prime }}\cap X=\emptyset $
.
Lemma 4.2.
-
(1) If
 $\mathcal {A}$
be an independent family, then
$\mathcal {A}$
be an independent family, then
 $\operatorname {\mathrm {id}}_{<\omega , \kappa }(\mathcal {A})$
is an ideal.
$\operatorname {\mathrm {id}}_{<\omega , \kappa }(\mathcal {A})$
is an ideal. -
(2) If
 $\mathcal {A}_{0},\mathcal {A}_{1}$
are independent families such that
$\mathcal {A}_{0},\mathcal {A}_{1}$
are independent families such that
 $\mathcal {A}_{0}\subseteq \mathcal {A}_{1}$
, then
$\mathcal {A}_{0}\subseteq \mathcal {A}_{1}$
, then
 $\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{0})\subseteq \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{1})$
.
$\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{0})\subseteq \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{1})$
.
Proof To prove item
![]() $(1)$
above consider any
$(1)$
above consider any
![]() $X_{0}$
and
$X_{0}$
and
![]() $X_{1}$
in
$X_{1}$
in
![]() $\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
. Fix any
$\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
. Fix any
![]() $h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
. Then there is
$h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
. Then there is
![]() $h_{0}\supseteq h$
such that
$h_{0}\supseteq h$
such that
![]() $\mathcal {A}^{h_{0}}\cap X_{0}=\emptyset $
and there is
$\mathcal {A}^{h_{0}}\cap X_{0}=\emptyset $
and there is
![]() $h_{1}\supseteq h_{0}$
such that
$h_{1}\supseteq h_{0}$
such that
![]() $\mathcal {A}^{h_{1}}\cap X_{1}=\emptyset $
. But then
$\mathcal {A}^{h_{1}}\cap X_{1}=\emptyset $
. But then
![]() $h_{1}\supseteq h$
and
$h_{1}\supseteq h$
and
![]() $\mathcal {A}^{h_{1}}\cap (X_{0}\cup X_{1})=\emptyset $
. Clearly,
$\mathcal {A}^{h_{1}}\cap (X_{0}\cup X_{1})=\emptyset $
. Clearly,
![]() $\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
is closed under subsets and thus
$\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
is closed under subsets and thus
![]() $\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
is an ideal.
$\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
is an ideal.
To prove item
![]() $(2)$
consider any
$(2)$
consider any
![]() $X\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{0})$
. Let
$X\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{0})$
. Let
![]() $h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}_{1})$
. Then
$h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}_{1})$
. Then
![]() $h^{\prime }=h\upharpoonright \mathcal {A}_{0}\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}_{0})$
and by hypothesis there is
$h^{\prime }=h\upharpoonright \mathcal {A}_{0}\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}_{0})$
and by hypothesis there is
![]() $h_{0}$
in
$h_{0}$
in
![]() $\operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}_{0})$
extending
$\operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}_{0})$
extending
![]() $h^{\prime }$
such that
$h^{\prime }$
such that
![]() $\mathcal {A}_{0}^{h_{0}}\cap X=\emptyset $
. Let
$\mathcal {A}_{0}^{h_{0}}\cap X=\emptyset $
. Let
![]() $h_{1}=h_{0}\cup h\upharpoonright (\mathcal {A}_{1}\backslash \mathcal {A}_{0})$
. Then
$h_{1}=h_{0}\cup h\upharpoonright (\mathcal {A}_{1}\backslash \mathcal {A}_{0})$
. Then
![]() $\mathcal {A}_{1}^{h_{1}}\cap X\subseteq \mathcal {A}_{0}^{h_{0}}\cap X$
and so
$\mathcal {A}_{1}^{h_{1}}\cap X\subseteq \mathcal {A}_{0}^{h_{0}}\cap X$
and so
![]() $\mathcal {A}_{1}^{h_{1}}\cap X=\emptyset $
.
$\mathcal {A}_{1}^{h_{1}}\cap X=\emptyset $
.
Remark 4.3. Note that
![]() $\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
is not necessarily
$\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
is not necessarily
![]() $\kappa $
-complete.
$\kappa $
-complete.
Lemma 4.4.
![]() $\Vdash _{\mathbb {P_{\mathcal {U}}}}\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})=\bigcup \{\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}):\exists A (\mathcal {A},A)\in G\}$
.
$\Vdash _{\mathbb {P_{\mathcal {U}}}}\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})=\bigcup \{\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}):\exists A (\mathcal {A},A)\in G\}$
.
Proof To see
![]() $\Vdash _{\mathbb {P}_{\mathcal {U}}}\bigcup \{\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}):\exists A(\mathcal {A},A)\in G\}\subseteq \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
consider any
$\Vdash _{\mathbb {P}_{\mathcal {U}}}\bigcup \{\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}):\exists A(\mathcal {A},A)\in G\}\subseteq \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
consider any
![]() $\mathbb {P}_{\mathcal {U}}$
-generic filter G. In
$\mathbb {P}_{\mathcal {U}}$
-generic filter G. In
![]() $V[G]$
we have
$V[G]$
we have
![]() $\mathcal {A}_{G}=\bigcup \{\mathcal {A}:\exists A(\mathcal {A},A)\in G\}$
. Now for all
$\mathcal {A}_{G}=\bigcup \{\mathcal {A}:\exists A(\mathcal {A},A)\in G\}$
. Now for all
![]() $(\mathcal {A},A)\in G$
, by Lemma 4.2(2),
$(\mathcal {A},A)\in G$
, by Lemma 4.2(2),
![]() $\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})\subseteq \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
. Therefore
$\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})\subseteq \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
. Therefore
![]() $\bigcup \{\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}):\exists A(\mathcal {A},A)\in G\}\subseteq \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
.
$\bigcup \{\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}):\exists A(\mathcal {A},A)\in G\}\subseteq \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
.
The fact that
![]() $\Vdash _{\mathbb {P_{\mathcal {U}}}}\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})\subseteq \bigcup \{\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}):\exists \mathcal {A} (\mathcal {A},A)\in G\}$
follows from the
$\Vdash _{\mathbb {P_{\mathcal {U}}}}\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})\subseteq \bigcup \{\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}):\exists \mathcal {A} (\mathcal {A},A)\in G\}$
follows from the
![]() $\kappa ^{+}$
-closure of
$\kappa ^{+}$
-closure of
![]() $\mathbb {P}_{\mathcal {U}}$
. Consider any
$\mathbb {P}_{\mathcal {U}}$
. Consider any
![]() $p=(\mathcal {A},A)\in G$
and a
$p=(\mathcal {A},A)\in G$
and a
![]() $\mathbb {P}_{\mathcal {U}}$
-name
$\mathbb {P}_{\mathcal {U}}$
-name
![]() $\dot {X}$
for a subset of
$\dot {X}$
for a subset of
![]() $\kappa $
such that
$\kappa $
such that
![]() $p\Vdash \dot {X}\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
. Fix
$p\Vdash \dot {X}\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
. Fix
![]() $h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
. Then
$h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
. Then
Thus there is
![]() $(\mathcal {A}^{\prime },A^{\prime })\leq (\mathcal {A},A)$
such that
$(\mathcal {A}^{\prime },A^{\prime })\leq (\mathcal {A},A)$
such that
![]() $h^{\prime }\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}^{\prime })$
,
$h^{\prime }\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}^{\prime })$
,
![]() $h^{\prime }\supseteq h$
and
$h^{\prime }\supseteq h$
and
![]() $\mathcal {A}^{h^{\prime }}\cap X=\emptyset $
. Proceed inductively to construct a decreasing sequence
$\mathcal {A}^{h^{\prime }}\cap X=\emptyset $
. Proceed inductively to construct a decreasing sequence
![]() $\{(\mathcal {A}_{i},A_{i})\}_{i\in \kappa }$
of conditions below p such that if
$\{(\mathcal {A}_{i},A_{i})\}_{i\in \kappa }$
of conditions below p such that if
![]() $\mathcal {A}_{\kappa }=\bigcup _{i\in \kappa }\mathcal {A}_{i}$
then for all
$\mathcal {A}_{\kappa }=\bigcup _{i\in \kappa }\mathcal {A}_{i}$
then for all
![]() $h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}_{\kappa })$
there is
$h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}_{\kappa })$
there is
![]() $h^{\prime }\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}_{\kappa })$
extending h and such that
$h^{\prime }\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}_{\kappa })$
extending h and such that
![]() $\mathcal {A}^{h^{\prime }}\cap X=\emptyset $
. Thus
$\mathcal {A}^{h^{\prime }}\cap X=\emptyset $
. Thus
![]() $X\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{\kappa })$
. By the
$X\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{\kappa })$
. By the
![]() $\kappa ^{+}$
-closure of
$\kappa ^{+}$
-closure of
![]() $\mathbb {P}_{\mathcal {U}}$
, there is
$\mathbb {P}_{\mathcal {U}}$
, there is
![]() $p^{\prime }=(\mathcal {B},B)\in \mathbb {P}_{\mathcal {U}}$
which is an extension of all
$p^{\prime }=(\mathcal {B},B)\in \mathbb {P}_{\mathcal {U}}$
which is an extension of all
![]() $(\mathcal {A}_{i},A_{i})$
. Thus
$(\mathcal {A}_{i},A_{i})$
. Thus
![]() $X\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {B})$
,
$X\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {B})$
,
![]() $p^{\prime }\leq p$
and
$p^{\prime }\leq p$
and
Lemma 4.5. Let
![]() $(\mathcal {A},A)\in \mathbb {P}_{\mathcal {U}}$
and let
$(\mathcal {A},A)\in \mathbb {P}_{\mathcal {U}}$
and let
![]() $X\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
. Then
$X\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
. Then
![]() $(\mathcal {A},A\backslash X)\in \mathbb {P}_{\mathcal {U}}$
.
$(\mathcal {A},A\backslash X)\in \mathbb {P}_{\mathcal {U}}$
.
Proof It is sufficient to show that for each
![]() $h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
the set
$h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
the set
![]() $\mathcal {A}^{h}\cap (A\backslash X)$
is unbounded. Fix
$\mathcal {A}^{h}\cap (A\backslash X)$
is unbounded. Fix
![]() $h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
. Since
$h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
. Since
![]() $X\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
there is
$X\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
there is
![]() $h^{\prime }\supseteq h$
,
$h^{\prime }\supseteq h$
,
![]() $h^{\prime }\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
extending h such that
$h^{\prime }\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
extending h such that
![]() $\mathcal {A}^{h^{\prime }}\cap X=\emptyset $
. Thus
$\mathcal {A}^{h^{\prime }}\cap X=\emptyset $
. Thus
![]() $\mathcal {A}^{h^{\prime }}\subseteq \kappa \backslash X$
. However
$\mathcal {A}^{h^{\prime }}\subseteq \kappa \backslash X$
. However
Thus
![]() $\mathcal {A}^{h^{\prime }}\cap A=\mathcal {A}^{h^{\prime }}\cap A\cap X^{c}$
is unbounded. Therefore
$\mathcal {A}^{h^{\prime }}\cap A=\mathcal {A}^{h^{\prime }}\cap A\cap X^{c}$
is unbounded. Therefore
![]() $(\mathcal {A},A\backslash X)$
is a condition.
$(\mathcal {A},A\backslash X)$
is a condition.
Corollary 4.6. Let G be a
![]() $\mathbb {P}_{\mathcal {U}}$
-generic filter. Then in
$\mathbb {P}_{\mathcal {U}}$
-generic filter. Then in
![]() $V[G]$
the density ideal
$V[G]$
the density ideal
![]() $\operatorname {\mathrm {id}}(\mathcal {A}_{G})$
is generated by
$\operatorname {\mathrm {id}}(\mathcal {A}_{G})$
is generated by
![]() $\{\kappa \backslash A:\exists \mathcal {A}(\mathcal {A},A)\in G\}$
. That is
$\{\kappa \backslash A:\exists \mathcal {A}(\mathcal {A},A)\in G\}$
. That is
Proof Let G be a
![]() $\mathbb {P}_{\mathcal {U}}$
-generic filter. By Lemma 4.4,
$\mathbb {P}_{\mathcal {U}}$
-generic filter. By Lemma 4.4,
![]() $\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})=\bigcup \{\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}):\exists A(\mathcal {A},A)\in G\}$
. Let
$\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})=\bigcup \{\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}):\exists A(\mathcal {A},A)\in G\}$
. Let
![]() $\mathcal {I}_{G}$
be the ideal generated by
$\mathcal {I}_{G}$
be the ideal generated by
![]() $\{\kappa \backslash A:\exists \mathcal {A}(\mathcal {A},A)\in G\}$
.
$\{\kappa \backslash A:\exists \mathcal {A}(\mathcal {A},A)\in G\}$
.
First we will show that
![]() $\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})\subseteq \mathcal {I}_{G}$
. Let
$\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})\subseteq \mathcal {I}_{G}$
. Let
![]() $X\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
. Thus there is
$X\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
. Thus there is
![]() $(\mathcal {A},A)\in G$
such that
$(\mathcal {A},A)\in G$
such that
![]() $X\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
. However the set
$X\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
. However the set
![]() $D_{X}=\{(\mathcal {B},B)\in \mathbb {P}_{\mathcal {U}}: X\cap B=\emptyset \}$
is dense below
$D_{X}=\{(\mathcal {B},B)\in \mathbb {P}_{\mathcal {U}}: X\cap B=\emptyset \}$
is dense below
![]() $(\mathcal {A},A)$
(indeed, if
$(\mathcal {A},A)$
(indeed, if
![]() $(\mathcal {B},B)\leq (\mathcal {A},A)$
then
$(\mathcal {B},B)\leq (\mathcal {A},A)$
then
![]() $X\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {B})$
and by Lemma 4.5
$X\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {B})$
and by Lemma 4.5
![]() $(\mathcal {B},B\backslash X)\leq (\mathcal {B},B)$
) and so there is
$(\mathcal {B},B\backslash X)\leq (\mathcal {B},B)$
) and so there is
![]() $(\mathcal {B},B)\in G$
such that
$(\mathcal {B},B)\in G$
such that
![]() $X\cap B=\emptyset $
. That is
$X\cap B=\emptyset $
. That is
![]() $X\subseteq \kappa \backslash B$
and so
$X\subseteq \kappa \backslash B$
and so
![]() $X\in \mathcal {I}_{G}$
.
$X\in \mathcal {I}_{G}$
.
To show that
![]() $\mathcal {I}_{G}\subseteq \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
, consider any
$\mathcal {I}_{G}\subseteq \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
, consider any
![]() $X\in \mathcal {I}_{G}$
. Then there is a finite set of conditions
$X\in \mathcal {I}_{G}$
. Then there is a finite set of conditions
![]() $\{(\mathcal {A}_{i},A_{i})\}_{i\in n}$
in G such that
$\{(\mathcal {A}_{i},A_{i})\}_{i\in n}$
in G such that
![]() $X\subseteq \bigcup _{i\in n}\kappa \backslash A_{i}=\kappa \backslash \bigcap _{i\in n}A_{i}$
. Note that
$X\subseteq \bigcup _{i\in n}\kappa \backslash A_{i}=\kappa \backslash \bigcap _{i\in n}A_{i}$
. Note that
![]() $(\mathcal {B},B)\in G$
, where
$(\mathcal {B},B)\in G$
, where
![]() $(\mathcal {B},B)=(\bigcup _{i\in n} \mathcal {A}_{i}, \bigcap _{i\in n} A_{i})$
. Thus
$(\mathcal {B},B)=(\bigcup _{i\in n} \mathcal {A}_{i}, \bigcap _{i\in n} A_{i})$
. Thus
![]() $X\subseteq \kappa \backslash B$
. Fix any
$X\subseteq \kappa \backslash B$
. Fix any
![]() $h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
. Then there is
$h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
. Then there is
![]() $(\mathcal {C},C)\in G$
such that
$(\mathcal {C},C)\in G$
such that
![]() $h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {C})$
. Take
$h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {C})$
. Take
![]() $(\mathcal {E},E)\in G$
which is a common extension of
$(\mathcal {E},E)\in G$
which is a common extension of
![]() $(\mathcal {B},B)$
and
$(\mathcal {B},B)$
and
![]() $(\mathcal {C},C)$
. Then
$(\mathcal {C},C)$
. Then
![]() $(\mathcal {E}, E)\leq (\mathcal {C}, B)$
and so in particular
$(\mathcal {E}, E)\leq (\mathcal {C}, B)$
and so in particular
![]() $(\mathcal {C},B)\in G$
. However the set
$(\mathcal {C},B)\in G$
. However the set
![]() $H_{B}=\{(\mathcal {C}^{\prime },C^{\prime }):\exists Y\in \mathcal {C}^{\prime }(Y\subseteq B)\}$
is dense below
$H_{B}=\{(\mathcal {C}^{\prime },C^{\prime }):\exists Y\in \mathcal {C}^{\prime }(Y\subseteq B)\}$
is dense below
![]() $(\mathcal {C},B)$
(apply Lemma 3.3) and so there is
$(\mathcal {C},B)$
(apply Lemma 3.3) and so there is
![]() $(\mathcal {C}^{\prime },C^{\prime })\in G$
such that for some
$(\mathcal {C}^{\prime },C^{\prime })\in G$
such that for some
![]() $Y\in \mathcal {C}^{\prime }$
,
$Y\in \mathcal {C}^{\prime }$
,
![]() $Y\subseteq B$
. Then
$Y\subseteq B$
. Then
![]() $h^{\prime }=h\cup \{(Y,0)\}\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
and
$h^{\prime }=h\cup \{(Y,0)\}\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
and
![]() $\mathcal {A}_{G}^{h^{\prime }}\cap X=\emptyset $
. Thus
$\mathcal {A}_{G}^{h^{\prime }}\cap X=\emptyset $
. Thus
![]() $X\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
.
$X\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
.
5 The density filter
Of particular interest for our investigations will be the dual filter of the density ideal. Note that the density filter plays an important role in the original work of [Reference Shelah22] on the relative consistency of
![]() $\mathfrak {i}<\mathfrak {u}$
, from which the existence of a Sacks indestructible maximal independent family can be extracted (see also [Reference Fischer and Montoya11]).
$\mathfrak {i}<\mathfrak {u}$
, from which the existence of a Sacks indestructible maximal independent family can be extracted (see also [Reference Fischer and Montoya11]).
Remark 5.1. Let G be
![]() $\mathbb {P}_{\mathcal {U}}$
-generic, let
$\mathbb {P}_{\mathcal {U}}$
-generic, let
![]() $\mathcal {F}_{G}=\{A:\exists \mathcal {A}\text { such that }(\mathcal {A},A)\in G\}$
, and let
$\mathcal {F}_{G}=\{A:\exists \mathcal {A}\text { such that }(\mathcal {A},A)\in G\}$
, and let
![]() $\operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
be the dual filter of
$\operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
be the dual filter of
![]() $\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
. By Corollary 4.6,
$\operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
. By Corollary 4.6,
![]() $\operatorname {\mathrm {fil}}_{<\omega , G}(\mathcal {A}_{G})$
is generated by
$\operatorname {\mathrm {fil}}_{<\omega , G}(\mathcal {A}_{G})$
is generated by
![]() $\mathcal {F}_{G}$
.
$\mathcal {F}_{G}$
.
Lemma 5.2. Let
![]() $(\mathcal {A},A)\in \mathbb {P}_{\mathcal {U}}$
,
$(\mathcal {A},A)\in \mathbb {P}_{\mathcal {U}}$
,
![]() $Y\in [\kappa ]^{\kappa }$
and
$Y\in [\kappa ]^{\kappa }$
and
![]() $h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
. Then there is
$h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
. Then there is
![]() $h^{*}\supseteq h$
in
$h^{*}\supseteq h$
in
![]() $\operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
and
$\operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
and
![]() $B\subseteq A$
such that
$B\subseteq A$
such that
![]() $(\mathcal {A},B)\leq (\mathcal {A},A)$
and
$(\mathcal {A},B)\leq (\mathcal {A},A)$
and
![]() $\mathcal {A}^{h^{*}}\cap B$
is contained either in Y, or in
$\mathcal {A}^{h^{*}}\cap B$
is contained either in Y, or in
![]() $\kappa \backslash Y$
.
$\kappa \backslash Y$
.
Proof If there is
![]() $h^{\prime }$
extending h such that
$h^{\prime }$
extending h such that
![]() $\mathcal {A}^{h^{\prime }}\cap A\cap Y$
is bounded, then
$\mathcal {A}^{h^{\prime }}\cap A\cap Y$
is bounded, then
![]() $\mathcal {A}^{h^{\prime }}\cap A=^{*} \mathcal {A}^{h^{\prime }}\cap A\cap (\kappa \backslash Y)$
and so for all
$\mathcal {A}^{h^{\prime }}\cap A=^{*} \mathcal {A}^{h^{\prime }}\cap A\cap (\kappa \backslash Y)$
and so for all
![]() $h^{\prime \prime }\supseteq h^{\prime }$
the set
$h^{\prime \prime }\supseteq h^{\prime }$
the set
![]() $\mathcal {A}^{h^{\prime \prime }}\cap A\cap (\kappa \backslash Y)$
is unbounded. Then take
$\mathcal {A}^{h^{\prime \prime }}\cap A\cap (\kappa \backslash Y)$
is unbounded. Then take
![]() $B=(\mathcal {A}^{h^{\prime }}\cap A\cap (\kappa \backslash Y))\cup (A\backslash \mathcal {A}^{h^{\prime }})$
. Then
$B=(\mathcal {A}^{h^{\prime }}\cap A\cap (\kappa \backslash Y))\cup (A\backslash \mathcal {A}^{h^{\prime }})$
. Then
![]() $B=^{*} A$
and so
$B=^{*} A$
and so
![]() $B\in \mathcal {U}$
,
$B\in \mathcal {U}$
,
![]() $(\mathcal {A},B)$
is as desired.
$(\mathcal {A},B)$
is as desired.
If there is
![]() $h^{\prime }\supseteq h$
such that
$h^{\prime }\supseteq h$
such that
![]() $\mathcal {A}^{h^{\prime }}\cap A\cap (\kappa \backslash Y)$
is bounded, then
$\mathcal {A}^{h^{\prime }}\cap A\cap (\kappa \backslash Y)$
is bounded, then
![]() $\mathcal {A}^{h^{\prime }}\cap A=^{*} \mathcal {A}^{h^{\prime }}\cap A\cap Y$
and so for all
$\mathcal {A}^{h^{\prime }}\cap A=^{*} \mathcal {A}^{h^{\prime }}\cap A\cap Y$
and so for all
![]() $h^{\prime \prime }\supseteq h^{\prime }$
the set
$h^{\prime \prime }\supseteq h^{\prime }$
the set
![]() $\mathcal {A}^{h^{\prime \prime }}\cap A\cap Y$
is unbounded. Then take
$\mathcal {A}^{h^{\prime \prime }}\cap A\cap Y$
is unbounded. Then take
![]() $B=(\mathcal {A}^{h^{\prime }}\cap A\cap Y)\cup (A\backslash \mathcal {A}^{h^{\prime }})$
. Then
$B=(\mathcal {A}^{h^{\prime }}\cap A\cap Y)\cup (A\backslash \mathcal {A}^{h^{\prime }})$
. Then
![]() $B=^{*} A$
and so
$B=^{*} A$
and so
![]() $B\in \mathcal {U}$
, and the condition
$B\in \mathcal {U}$
, and the condition
![]() $(\mathcal {A},B)$
is as desired.
$(\mathcal {A},B)$
is as desired.
Suppose, none of the above two cases holds. Thus for every
![]() $h^{\prime }\supseteq h$
, the sets
$h^{\prime }\supseteq h$
, the sets
![]() $\mathcal {A}^{h^{\prime }}\cap A\cap Y$
and
$\mathcal {A}^{h^{\prime }}\cap A\cap Y$
and
![]() $\mathcal {A}^{h^{\prime }}\cap A\cap (\kappa \backslash Y)$
are unbounded. Then each of the sets
$\mathcal {A}^{h^{\prime }}\cap A\cap (\kappa \backslash Y)$
are unbounded. Then each of the sets
![]() $B_{0}=(\mathcal {A}^{h}\cap A\cap Y)\cup (A\backslash \mathcal {A}^{h})$
and
$B_{0}=(\mathcal {A}^{h}\cap A\cap Y)\cup (A\backslash \mathcal {A}^{h})$
and
![]() $B_{1}=(\mathcal {A}^{h}\cap A\cap (\kappa \backslash Y))\cup (A\backslash \mathcal {A}^{h})$
meets every Boolean combination
$B_{1}=(\mathcal {A}^{h}\cap A\cap (\kappa \backslash Y))\cup (A\backslash \mathcal {A}^{h})$
meets every Boolean combination
![]() $\mathcal {A}^{h^{\prime }}$
for
$\mathcal {A}^{h^{\prime }}$
for
![]() $h^{\prime }\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
on an unbounded set. Thus if
$h^{\prime }\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
on an unbounded set. Thus if
![]() $A\backslash \mathcal {A}^{h}\in \mathcal {U}$
, both B and
$A\backslash \mathcal {A}^{h}\in \mathcal {U}$
, both B and
![]() $B^{\prime }$
are as desired. Suppose
$B^{\prime }$
are as desired. Suppose
![]() $A\backslash \mathcal {A}^{h}\notin \mathcal {U}$
. Then
$A\backslash \mathcal {A}^{h}\notin \mathcal {U}$
. Then
![]() $A\cap \mathcal {A}^{h}\in \mathcal {U}$
and so either
$A\cap \mathcal {A}^{h}\in \mathcal {U}$
and so either
![]() $A\cap \mathcal {A}^{h}\cap Y$
or
$A\cap \mathcal {A}^{h}\cap Y$
or
![]() $A\cap \mathcal {A}^{h}\cap (\kappa \backslash Y)$
is in the normal measure. We can choose appropriately.
$A\cap \mathcal {A}^{h}\cap (\kappa \backslash Y)$
is in the normal measure. We can choose appropriately.
Corollary 5.3. Let
![]() $\mathcal {E}=\{Y,\kappa \backslash Y\}$
be a partition. Then the set of
$\mathcal {E}=\{Y,\kappa \backslash Y\}$
be a partition. Then the set of
![]() $(\mathcal {A},A)\in \mathbb {P}_{\mathcal {U}}$
such that for each
$(\mathcal {A},A)\in \mathbb {P}_{\mathcal {U}}$
such that for each
![]() $h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
there is
$h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
there is
![]() $h^{\prime }\supseteq h$
in
$h^{\prime }\supseteq h$
in
![]() $\operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
with the property that
$\operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
with the property that
![]() $\mathcal {A}^{h^{\prime }}$
is either contained in Y, or in
$\mathcal {A}^{h^{\prime }}$
is either contained in Y, or in
![]() $\kappa \backslash Y$
is dense in
$\kappa \backslash Y$
is dense in
![]() $\mathbb {P}_{\mathcal {U}}$
.
$\mathbb {P}_{\mathcal {U}}$
.
Proof Consider an arbitrary
![]() $(\mathcal {A},A)\in \mathbb {P}_{\mathcal {U}}$
. Fix
$(\mathcal {A},A)\in \mathbb {P}_{\mathcal {U}}$
. Fix
![]() $h_{0}\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
. Then there is
$h_{0}\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
. Then there is
![]() $A_{0}\subseteq A$
such that
$A_{0}\subseteq A$
such that
![]() $(\mathcal {A},A_{0})\leq (\mathcal {A},A)$
and there is
$(\mathcal {A},A_{0})\leq (\mathcal {A},A)$
and there is
![]() $h_{1}\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
extending
$h_{1}\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
extending
![]() $h_{0}$
and
$h_{0}$
and
![]() $B\subseteq A$
such that
$B\subseteq A$
such that
![]() $\mathcal {A}^{h_{1}}\cap B$
is contained either in Y, or in
$\mathcal {A}^{h_{1}}\cap B$
is contained either in Y, or in
![]() $\kappa \backslash Y$
. However, by Lemma 3.3 there is
$\kappa \backslash Y$
. However, by Lemma 3.3 there is
![]() $B_{0}\subseteq B$
such that
$B_{0}\subseteq B$
such that
![]() $(\mathcal {A}\cup \{B_{0}\},B)\leq (\mathcal {A}, B)$
. Then extend
$(\mathcal {A}\cup \{B_{0}\},B)\leq (\mathcal {A}, B)$
. Then extend
![]() $h_{1}$
to
$h_{1}$
to
![]() $h_{1}^{\prime }=h_{1}\cup \{(B_{0},0)\}$
and note that
$h_{1}^{\prime }=h_{1}\cup \{(B_{0},0)\}$
and note that
![]() $h_{1}^{\prime }\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}_{1})$
, where
$h_{1}^{\prime }\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}_{1})$
, where
![]() $\mathcal {A}_{1}=\mathcal {A}\cup \{B_{0}\}$
, and that
$\mathcal {A}_{1}=\mathcal {A}\cup \{B_{0}\}$
, and that
![]() $\mathcal {A}_{1}^{h_{1}^{\prime }}$
is either contained in Y or in
$\mathcal {A}_{1}^{h_{1}^{\prime }}$
is either contained in Y or in
![]() $\kappa \backslash Y$
. Proceed inductively and use the fact that
$\kappa \backslash Y$
. Proceed inductively and use the fact that
![]() $\mathbb {P}_{\mathcal {U}}$
is
$\mathbb {P}_{\mathcal {U}}$
is
![]() $\kappa ^{+}$
-closed.
$\kappa ^{+}$
-closed.
Definition 5.4. Let
![]() $\mathcal {F}\subseteq [\kappa ]^{\kappa }$
. We say that
$\mathcal {F}\subseteq [\kappa ]^{\kappa }$
. We say that
![]() $\mathcal {F}$
is a
$\mathcal {F}$
is a
![]() $\kappa \text {-P-set}$
if every
$\kappa \text {-P-set}$
if every
![]() $\mathcal {H}\subseteq \mathcal {F}$
of cardinality
$\mathcal {H}\subseteq \mathcal {F}$
of cardinality
![]() $\leq \kappa $
has a pseudo-intersection in
$\leq \kappa $
has a pseudo-intersection in
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
Lemma 5.5. Let G be a
![]() $\mathbb {P}_{\mathcal {U}}$
-generic filter. Then
$\mathbb {P}_{\mathcal {U}}$
-generic filter. Then
![]() $\mathcal {F}_{G}$
is a
$\mathcal {F}_{G}$
is a
![]() $\kappa \mathrm{-P-}{set}$
.
$\kappa \mathrm{-P-}{set}$
.
Proof Suppose
![]() $\mathcal {F}_{G}$
is not a
$\mathcal {F}_{G}$
is not a
![]() $\kappa \text {-P-set}$
. Thus there is
$\kappa \text {-P-set}$
. Thus there is
![]() $p\in \mathbb {P}_{\mathcal {U}}$
such that
$p\in \mathbb {P}_{\mathcal {U}}$
such that
Fix G a
![]() $\mathbb {P}_{\mathcal {U}}$
-generic filter such that
$\mathbb {P}_{\mathcal {U}}$
-generic filter such that
![]() $p\in G$
. Since
$p\in G$
. Since
![]() $\mathbb {P}_{\mathcal {U}}$
is
$\mathbb {P}_{\mathcal {U}}$
is
![]() $\kappa ^{+}$
-closed, we can find
$\kappa ^{+}$
-closed, we can find
![]() $\mathcal {H}^{\prime }=\{A_{i}\}_{i\in \kappa }$
in the ground model witnessing the above property. For each
$\mathcal {H}^{\prime }=\{A_{i}\}_{i\in \kappa }$
in the ground model witnessing the above property. For each
![]() $i\in \kappa $
, let
$i\in \kappa $
, let
![]() $\mathcal {A}_{i}$
be such that
$\mathcal {A}_{i}$
be such that
![]() $(\mathcal {A}_{i}, A_{i})\in G$
. We can assume that
$(\mathcal {A}_{i}, A_{i})\in G$
. We can assume that
![]() $\tau =\{(\mathcal {A}_{i},A_{i})\}_{i\in \kappa }$
is decreasing and that
$\tau =\{(\mathcal {A}_{i},A_{i})\}_{i\in \kappa }$
is decreasing and that
![]() $(\mathcal {A}_{0},A_{0})\leq p$
. Now, take
$(\mathcal {A}_{0},A_{0})\leq p$
. Now, take
![]() $q=(\mathcal {A},A)$
in
$q=(\mathcal {A},A)$
in
![]() $\mathbb {P}_{\mathcal {U}}$
to be a common lower bound of
$\mathbb {P}_{\mathcal {U}}$
to be a common lower bound of
![]() $\tau $
. Then
$\tau $
. Then
![]() $q\leq p$
and q forces that A is a pseudo-intersection of
$q\leq p$
and q forces that A is a pseudo-intersection of
![]() $\mathcal {H}^{\prime }$
, which is a contradiction.
$\mathcal {H}^{\prime }$
, which is a contradiction.
5.1 Increasing functions and the density filter
In the countable setting a key feature of the Sacks indestructible maximal independent family appearing in [Reference Shelah22] is the fact that the associated density filter is a Q-set. The existence of sufficiently fast growing sets in
![]() $\operatorname {\mathrm {fil}}_{<\omega , \kappa }(\mathcal {A}_{G})$
, which we discuss in this section, will be of vital importance for our main result.
$\operatorname {\mathrm {fil}}_{<\omega , \kappa }(\mathcal {A}_{G})$
, which we discuss in this section, will be of vital importance for our main result.
If
![]() $E\subseteq \kappa $
is an unbounded set and for each
$E\subseteq \kappa $
is an unbounded set and for each
![]() $\alpha \in \kappa $
let
$\alpha \in \kappa $
let
![]() $s_{E}(\alpha )=\min \{\beta \in E: \beta>\alpha \}$
.
$s_{E}(\alpha )=\min \{\beta \in E: \beta>\alpha \}$
.
Lemma 5.6. Let
![]() $f\in V\cap {^{\kappa }\kappa }$
be a strictly increasing function and let
$f\in V\cap {^{\kappa }\kappa }$
be a strictly increasing function and let
![]() $(\mathcal {A},A)\in \mathbb {P}_{\mathcal {U}}$
. Then there is
$(\mathcal {A},A)\in \mathbb {P}_{\mathcal {U}}$
. Then there is
![]() $A^{*}\subseteq A$
such that
$A^{*}\subseteq A$
such that
![]() $(\mathcal {A},A^{*})\leq (\mathcal {A},A)$
and if
$(\mathcal {A},A^{*})\leq (\mathcal {A},A)$
and if
![]() $\{a(i)\}_{i<\kappa }$
is the increasing enumeration of
$\{a(i)\}_{i<\kappa }$
is the increasing enumeration of
![]() $A^{*}$
then
$A^{*}$
then
![]() $f(a(i))<a(i+1)$
for all i.
$f(a(i))<a(i+1)$
for all i.
Proof Let
![]() $C_{f}=\{\xi <\kappa : \forall \zeta <\xi (f(\zeta )<\xi )\}$
. Thus
$C_{f}=\{\xi <\kappa : \forall \zeta <\xi (f(\zeta )<\xi )\}$
. Thus
![]() $C_{f}$
is a club and so
$C_{f}$
is a club and so
![]() $C_{f}\in \mathcal {U}$
. Then
$C_{f}\in \mathcal {U}$
. Then
![]() $E=A\cap C_{f}\in \mathcal {U}$
. Let
$E=A\cap C_{f}\in \mathcal {U}$
. Let
![]() $\{h_{i}\}_{i<\kappa }$
be an enumeration of the elements of
$\{h_{i}\}_{i<\kappa }$
be an enumeration of the elements of
![]() $\operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
such that each element occurs unboundedly often. The set
$\operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
such that each element occurs unboundedly often. The set
![]() $A^{*}$
will be constructed as the union of an increasing sequence
$A^{*}$
will be constructed as the union of an increasing sequence
![]() $\{B_{\xi }\}_{\xi <\kappa }$
of subsets of A.
$\{B_{\xi }\}_{\xi <\kappa }$
of subsets of A.
Let
![]() $B_{0}=\emptyset $
. If
$B_{0}=\emptyset $
. If
![]() $\mathcal {A}^{h_{0}}\cap E\neq \emptyset $
, let
$\mathcal {A}^{h_{0}}\cap E\neq \emptyset $
, let
![]() $a_{0}=\min \mathcal {A}^{h_{0}}\cap E$
. Otherwise, take
$a_{0}=\min \mathcal {A}^{h_{0}}\cap E$
. Otherwise, take
![]() $a_{0}=\min \mathcal {A}^{h_{0}}\cap A$
. Let
$a_{0}=\min \mathcal {A}^{h_{0}}\cap A$
. Let
Suppose we have defined
![]() $B_{\xi }$
. If
$B_{\xi }$
. If
![]() $(\mathcal {A}^{h_{\xi +1}}\cap E)\backslash (B_{\xi }\cup \{\sup B_{\xi }\})\neq \emptyset $
, let
$(\mathcal {A}^{h_{\xi +1}}\cap E)\backslash (B_{\xi }\cup \{\sup B_{\xi }\})\neq \emptyset $
, let
![]() $a_{\xi +1}=\min ((\mathcal {A}^{h_{\xi +1}}\cap E)\backslash (B_{\xi }\cup \{\sup B_{\xi }\}))$
. Otherwise, let
$a_{\xi +1}=\min ((\mathcal {A}^{h_{\xi +1}}\cap E)\backslash (B_{\xi }\cup \{\sup B_{\xi }\}))$
. Otherwise, let
![]() $a_{\xi +1}=\min \{a\in \mathcal {A}^{h_{\xi +1}}\cap A: a>\sup B_{\xi }\}$
. Let
$a_{\xi +1}=\min \{a\in \mathcal {A}^{h_{\xi +1}}\cap A: a>\sup B_{\xi }\}$
. Let
Now, suppose
![]() $\xi $
is a limit and for all
$\xi $
is a limit and for all
![]() $\zeta <\xi $
, the set
$\zeta <\xi $
, the set
![]() $B_{\zeta }$
has been defined. Take
$B_{\zeta }$
has been defined. Take
![]() $B_{\xi }^{*}=\bigcup _{\zeta <\xi } B_{\zeta }$
. If
$B_{\xi }^{*}=\bigcup _{\zeta <\xi } B_{\zeta }$
. If
![]() $(\mathcal {A}^{h_{\xi }}\cap E)\backslash (B_{\xi }^{*}\cup \{\sup B_{\xi }^{*}\})\neq \emptyset $
, let
$(\mathcal {A}^{h_{\xi }}\cap E)\backslash (B_{\xi }^{*}\cup \{\sup B_{\xi }^{*}\})\neq \emptyset $
, let
![]() $a_{\xi }=\min (\mathcal {A}^{h_{\xi }}\cap E)\backslash (B_{\xi }^{*}\cup \{\sup B_{\xi }^{*}\})\neq \emptyset $
. Otherwise, let
$a_{\xi }=\min (\mathcal {A}^{h_{\xi }}\cap E)\backslash (B_{\xi }^{*}\cup \{\sup B_{\xi }^{*}\})\neq \emptyset $
. Otherwise, let
![]() $a_{\xi }=\min \{a\in \mathcal {A}^{h_{\xi }}\cap A: a>\sup B^{*}_{\xi }\}$
. Let
$a_{\xi }=\min \{a\in \mathcal {A}^{h_{\xi }}\cap A: a>\sup B^{*}_{\xi }\}$
. Let
Finally, take
![]() $A^{*}=\bigcup _{\xi <\kappa } B_{\xi }$
. Then
$A^{*}=\bigcup _{\xi <\kappa } B_{\xi }$
. Then
![]() $A^{*}$
meets every Boolean combination
$A^{*}$
meets every Boolean combination
![]() $\mathcal {A}^{h}$
of
$\mathcal {A}^{h}$
of
![]() $\mathcal {A}$
on an unbounded set (witnessed by the
$\mathcal {A}$
on an unbounded set (witnessed by the
![]() $a_{\xi }$
’s),
$a_{\xi }$
’s),
![]() $A^{*}\subseteq A$
and since
$A^{*}\subseteq A$
and since
![]() $\{a_{\xi }\}_{\xi <\kappa }$
is unbounded in
$\{a_{\xi }\}_{\xi <\kappa }$
is unbounded in
![]() $\kappa $
and
$\kappa $
and
for each
![]() $\xi $
, we also have that
$\xi $
, we also have that
![]() $E\subseteq A^{*}$
. Let
$E\subseteq A^{*}$
. Let
![]() $b<a$
be elements of
$b<a$
be elements of
![]() $A^{*}$
. If
$A^{*}$
. If
![]() $a\in E$
, then by definition of
$a\in E$
, then by definition of
![]() $C_{f}$
we have that
$C_{f}$
we have that
![]() $f(b)<a$
. If
$f(b)<a$
. If
![]() $a\notin E$
and
$a\notin E$
and
![]() $a=a_{\xi +1}$
for some
$a=a_{\xi +1}$
for some
![]() $\xi $
, then
$\xi $
, then
by construction. If
![]() $\xi $
is a limit,
$\xi $
is a limit,
![]() $a=a_{\xi }$
and
$a=a_{\xi }$
and
![]() $f(a_{\zeta })<s_{E}(f(a_{\zeta }))<a_{\xi }$
for each
$f(a_{\zeta })<s_{E}(f(a_{\zeta }))<a_{\xi }$
for each
![]() $\zeta <\xi $
again by construction. Since
$\zeta <\xi $
again by construction. Since
![]() $b=a_{\zeta }$
for some
$b=a_{\zeta }$
for some
![]() $\zeta <\xi $
,
$\zeta <\xi $
,
![]() $f(b)<a$
.
$f(b)<a$
.
The following corollary will play an important role in the main result of the paper.
Corollary 5.7. Let G be
![]() $\mathbb {P}_{\mathcal {U}}$
-generic,
$\mathbb {P}_{\mathcal {U}}$
-generic,
![]() $f\in V\cap {^{\kappa }\kappa }$
be strictly increasing. Then there is
$f\in V\cap {^{\kappa }\kappa }$
be strictly increasing. Then there is
![]() $A\in \operatorname {\mathrm {fil}}_{<\omega , \kappa }(\mathcal {A}_{G})$
such that if
$A\in \operatorname {\mathrm {fil}}_{<\omega , \kappa }(\mathcal {A}_{G})$
such that if
![]() $\{a(i)\}_{i\in \kappa }$
is the increasing enumeration of A then
$\{a(i)\}_{i\in \kappa }$
is the increasing enumeration of A then
![]() $f(a(i))<a(i+1)$
for all
$f(a(i))<a(i+1)$
for all
![]() $i \in \kappa $
.
$i \in \kappa $
.
Proof Since
![]() $\operatorname {\mathrm {fil}}_{<\omega , \kappa }(\mathcal {A}_{G})$
is generated by
$\operatorname {\mathrm {fil}}_{<\omega , \kappa }(\mathcal {A}_{G})$
is generated by
![]() $\mathcal {F}_{G}$
(the set of second coordinated of elements of the generic filter G) we may use the previous lemma and get the result.
$\mathcal {F}_{G}$
(the set of second coordinated of elements of the generic filter G) we may use the previous lemma and get the result.
Indeed, this is a standard density argument: Let
![]() $D_{f}$
be the set of all
$D_{f}$
be the set of all
![]() $(\mathcal {A},A)\in \mathbb {P}_{\mathcal {U}}$
such that if
$(\mathcal {A},A)\in \mathbb {P}_{\mathcal {U}}$
such that if
![]() $\{a(i)\}_{i<\kappa }$
is the enumeration function of A then
$\{a(i)\}_{i<\kappa }$
is the enumeration function of A then
![]() $f(a(i))< a(i+1)$
for all
$f(a(i))< a(i+1)$
for all
![]() $i<\kappa $
. By Lemma 5.6 the set
$i<\kappa $
. By Lemma 5.6 the set
![]() $D_{f}$
is dense. Thus,
$D_{f}$
is dense. Thus,
![]() $G\cap D_{f}\neq \emptyset $
and so there is
$G\cap D_{f}\neq \emptyset $
and so there is
![]() $(\mathcal {A},A)\in G\cap D_{f}$
. But, by definition of the set
$(\mathcal {A},A)\in G\cap D_{f}$
. But, by definition of the set
![]() $\mathcal {F}_{G}$
, we have that
$\mathcal {F}_{G}$
, we have that
![]() $A\in \mathcal {F}_{G}$
(see also Remark 5.1), and by the same remark
$A\in \mathcal {F}_{G}$
(see also Remark 5.1), and by the same remark
![]() $A\in \operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
. Since
$A\in \operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
. Since
![]() $(\mathcal {A}, A)\in D_{f}$
, we obtain that
$(\mathcal {A}, A)\in D_{f}$
, we obtain that
![]() $f(a(i))<a(i+1)$
.
$f(a(i))<a(i+1)$
.
6 Dense maximality
The notion of densely maximal independent families on
![]() $\omega $
appears for the first time in [Reference Goldstern and Shelah16]. Moreover, the maximal independent family constructed in [Reference Shelah22] which becomes a witness to
$\omega $
appears for the first time in [Reference Goldstern and Shelah16]. Moreover, the maximal independent family constructed in [Reference Shelah22] which becomes a witness to
![]() $\mathfrak {i}=\aleph _{1}$
in the model of [Reference Shelah22, Theorem 3.1] is densely maximal. A similar notion will play a vital role for our considerations:
$\mathfrak {i}=\aleph _{1}$
in the model of [Reference Shelah22, Theorem 3.1] is densely maximal. A similar notion will play a vital role for our considerations:
Definition 6.1. An independent family
![]() $\mathcal {A}$
is said to be densely maximal if for every
$\mathcal {A}$
is said to be densely maximal if for every
![]() $X\in [\kappa ]^{\kappa }\backslash \mathcal {A}$
and every
$X\in [\kappa ]^{\kappa }\backslash \mathcal {A}$
and every
![]() $h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
there is
$h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
there is
![]() $h^{\prime }\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
extending h such that either
$h^{\prime }\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
extending h such that either
![]() $\mathcal {A}^{h^{\prime }}\cap X=\emptyset $
or
$\mathcal {A}^{h^{\prime }}\cap X=\emptyset $
or
![]() $\mathcal {A}^{h^{\prime }}\cap (\kappa \backslash X)=\emptyset $
.
$\mathcal {A}^{h^{\prime }}\cap (\kappa \backslash X)=\emptyset $
.
The following characterization of dense maximality on
![]() $\omega $
appears implicitly in the proof of [Reference Shelah22, Theorem 3.1]. This characterization will be the main tool in showing that a specially designed normal measure supported
$\omega $
appears implicitly in the proof of [Reference Shelah22, Theorem 3.1]. This characterization will be the main tool in showing that a specially designed normal measure supported
![]() $\kappa $
-maximal independent family preserves its maximality after forcing with a large product of
$\kappa $
-maximal independent family preserves its maximality after forcing with a large product of
![]() $\kappa $
-Sacks forcing.
$\kappa $
-Sacks forcing.
Lemma 6.2. Let
![]() $\mathcal {A}$
be an independent family. Then
$\mathcal {A}$
be an independent family. Then
![]() $\mathcal {A}$
is densely maximal if and only if
$\mathcal {A}$
is densely maximal if and only if
![]() $(\ast )\ \forall h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}) \forall X\subseteq \mathcal {A}^{h}$
either there is
$(\ast )\ \forall h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}) \forall X\subseteq \mathcal {A}^{h}$
either there is
![]() $B\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
such that
$B\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
such that
![]() $\mathcal {A}^{h}\backslash X\subseteq B$
, or there is
$\mathcal {A}^{h}\backslash X\subseteq B$
, or there is
![]() $h^{\prime }\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
such that
$h^{\prime }\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
such that
![]() $h^{\prime }\supseteq h$
and
$h^{\prime }\supseteq h$
and
![]() $\mathcal {A}^{h^{\prime }}\subseteq \mathcal {A}^{h}\backslash X$
.
$\mathcal {A}^{h^{\prime }}\subseteq \mathcal {A}^{h}\backslash X$
.
Proof Suppose
![]() $\mathcal {A}$
satisfies property
$\mathcal {A}$
satisfies property
![]() $(\ast )$
. Let
$(\ast )$
. Let
![]() $X\in [\kappa ]^{\kappa }$
,
$X\in [\kappa ]^{\kappa }$
,
![]() $h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
and consider
$h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
and consider
![]() $Y=X\cap \mathcal {A}^{h}$
. Apply property
$Y=X\cap \mathcal {A}^{h}$
. Apply property
![]() $(*)$
. If there is
$(*)$
. If there is
![]() $B\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
such that
$B\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
such that
![]() $\mathcal {A}^{h}\backslash X\subseteq B$
, then
$\mathcal {A}^{h}\backslash X\subseteq B$
, then
![]() $\mathcal {A}^{h}\backslash X\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
. Then there is
$\mathcal {A}^{h}\backslash X\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
. Then there is
![]() $h^{\prime }\supseteq h$
such that
$h^{\prime }\supseteq h$
such that
![]() $\mathcal {A}^{h^{\prime }}\cap (\mathcal {A}^{h}\backslash X)=\mathcal {A}^{h^{\prime }}\backslash X=\emptyset $
. If there is
$\mathcal {A}^{h^{\prime }}\cap (\mathcal {A}^{h}\backslash X)=\mathcal {A}^{h^{\prime }}\backslash X=\emptyset $
. If there is
![]() $h^{\prime }\supseteq h$
such that
$h^{\prime }\supseteq h$
such that
![]() $\mathcal {A}^{h^{\prime }}\subseteq \mathcal {A}^{h}\backslash X$
, then
$\mathcal {A}^{h^{\prime }}\subseteq \mathcal {A}^{h}\backslash X$
, then
![]() $\mathcal {A}^{h^{\prime }}\cap X=\emptyset $
. Thus
$\mathcal {A}^{h^{\prime }}\cap X=\emptyset $
. Thus
![]() $\mathcal {A}$
is densely maximal.
$\mathcal {A}$
is densely maximal.
Now suppose
![]() $\mathcal {A}$
is densely maximal. Fix
$\mathcal {A}$
is densely maximal. Fix
![]() $h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
such that
$h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
such that
![]() $X\subseteq \mathcal {A}^{h}$
. We will show that
$X\subseteq \mathcal {A}^{h}$
. We will show that
![]() $\mathcal {A}$
satisfies property
$\mathcal {A}$
satisfies property
![]() $(\ast )$
. Suppose, there is no
$(\ast )$
. Suppose, there is no
![]() $B\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
such that
$B\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
such that
![]() $\mathcal {A}^{h}\backslash X\subseteq B$
. Thus in particular
$\mathcal {A}^{h}\backslash X\subseteq B$
. Thus in particular
![]() $\mathcal {A}^{h}\backslash X\notin \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
and so there is
$\mathcal {A}^{h}\backslash X\notin \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
and so there is
![]() $h^{\prime }\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
such that for all
$h^{\prime }\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
such that for all
![]() $h^{\prime \prime }\supseteq h^{\prime }$
the set
$h^{\prime \prime }\supseteq h^{\prime }$
the set
![]() $\mathcal {A}^{h^{\prime \prime }}\cap (\mathcal {A}^{h}\backslash X)\neq \emptyset $
. If h and
$\mathcal {A}^{h^{\prime \prime }}\cap (\mathcal {A}^{h}\backslash X)\neq \emptyset $
. If h and
![]() $h^{\prime }$
are incompatible as conditions in
$h^{\prime }$
are incompatible as conditions in
![]() $\operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
, then
$\operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
, then
![]() $\mathcal {A}^{h^{\prime }}\cap (\mathcal {A}^{h}\backslash X)=\emptyset $
, which is a contradiction. Therefore h and
$\mathcal {A}^{h^{\prime }}\cap (\mathcal {A}^{h}\backslash X)=\emptyset $
, which is a contradiction. Therefore h and
![]() $h^{\prime }$
are compatible. Without loss of generality,
$h^{\prime }$
are compatible. Without loss of generality,
![]() $h^{\prime }\supseteq h$
(otherwise pass to a common extension of h and
$h^{\prime }\supseteq h$
(otherwise pass to a common extension of h and
![]() $h^{\prime }$
). Thus h has an extension, namely
$h^{\prime }$
). Thus h has an extension, namely
![]() $h^{\prime }$
, such that for all
$h^{\prime }$
, such that for all
![]() $h^{\prime \prime }\supseteq h^{\prime }$
the set
$h^{\prime \prime }\supseteq h^{\prime }$
the set
![]() $\mathcal {A}^{h^{\prime \prime }}\backslash X$
is non-empty. Apply the fact that
$\mathcal {A}^{h^{\prime \prime }}\backslash X$
is non-empty. Apply the fact that
![]() $\mathcal {A}$
is densely maximal to
$\mathcal {A}$
is densely maximal to
![]() $\mathcal {A}^{h^{\prime }}$
and X. Thus, there is
$\mathcal {A}^{h^{\prime }}$
and X. Thus, there is
![]() $h^{\prime \prime }\supseteq h^{\prime }$
such that
$h^{\prime \prime }\supseteq h^{\prime }$
such that
![]() $\mathcal {A}^{h^{\prime \prime }}\cap X=\emptyset $
. Therefore
$\mathcal {A}^{h^{\prime \prime }}\cap X=\emptyset $
. Therefore
![]() $\mathcal {A}^{h^{\prime \prime }}\subseteq \mathcal {A}^{h^{\prime }}\backslash X\subseteq \mathcal {A}^{h}\backslash X$
, which completes the proof of property
$\mathcal {A}^{h^{\prime \prime }}\subseteq \mathcal {A}^{h^{\prime }}\backslash X\subseteq \mathcal {A}^{h}\backslash X$
, which completes the proof of property
![]() $(\ast )$
.
$(\ast )$
.
Lemma 6.3. Let G be
![]() $\mathbb {P}_{\mathcal {U}}$
-generic. Then in
$\mathbb {P}_{\mathcal {U}}$
-generic. Then in
![]() $V_{0}=V[G]$
the family
$V_{0}=V[G]$
the family
![]() $\mathcal {A}_{G}:=\bigcup \{\mathcal {A}:\exists A(\mathcal {A},A)\in G\}$
is densely maximal.
$\mathcal {A}_{G}:=\bigcup \{\mathcal {A}:\exists A(\mathcal {A},A)\in G\}$
is densely maximal.
Proof It is sufficient to show that
![]() $\mathcal {A}_{G}$
satisfies property
$\mathcal {A}_{G}$
satisfies property
![]() $(\ast )$
from Lemma 6.2. Thus, fix h and X as in
$(\ast )$
from Lemma 6.2. Thus, fix h and X as in
![]() $(\ast )$
. Suppose there is no
$(\ast )$
. Suppose there is no
![]() $B\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
such that
$B\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
such that
![]() $\mathcal {A}_{G}^{h}\backslash X\subseteq B$
. Then, in particular
$\mathcal {A}_{G}^{h}\backslash X\subseteq B$
. Then, in particular
![]() $\mathcal {A}_{G}^{h}\backslash X\notin \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
and so there is
$\mathcal {A}_{G}^{h}\backslash X\notin \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
and so there is
![]() $h_{0}\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
such that for all
$h_{0}\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
such that for all
![]() $h_{1}\supseteq h_{0}$
the set
$h_{1}\supseteq h_{0}$
the set
![]() $\mathcal {A}^{h_{1}}\cap (\mathcal {A}^{h}\backslash X)\neq \emptyset $
(by definition of the density ideal). Consider the partition
$\mathcal {A}^{h_{1}}\cap (\mathcal {A}^{h}\backslash X)\neq \emptyset $
(by definition of the density ideal). Consider the partition
and the set
![]() $\mathcal {A}^{h_{0}}$
. By Corollary 5.3 there is
$\mathcal {A}^{h_{0}}$
. By Corollary 5.3 there is
![]() $h_{1}\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
extending
$h_{1}\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A}_{G})$
extending
![]() $h_{0}$
such that
$h_{0}$
such that
![]() $\mathcal {A}^{h_{1}}$
is contained in one element of
$\mathcal {A}^{h_{1}}$
is contained in one element of
![]() $\mathcal {E}$
. However, if
$\mathcal {E}$
. However, if
![]() $\mathcal {A}^{h_{1}}\subseteq \kappa \backslash (\mathcal {A}^{h}\backslash X)$
, then
$\mathcal {A}^{h_{1}}\subseteq \kappa \backslash (\mathcal {A}^{h}\backslash X)$
, then
![]() $\mathcal {A}^{h_{1}}\cap (\mathcal {A}^{h}\backslash X)=\emptyset $
, which is a contradiction to the choice of
$\mathcal {A}^{h_{1}}\cap (\mathcal {A}^{h}\backslash X)=\emptyset $
, which is a contradiction to the choice of
![]() $h_{0}$
. Thus
$h_{0}$
. Thus
![]() $\mathcal {A}^{h_{1}}\subseteq \mathcal {A}^{h}\backslash X$
and so
$\mathcal {A}^{h_{1}}\subseteq \mathcal {A}^{h}\backslash X$
and so
![]() $\mathcal {A}^{h_{1}}\cap X=\emptyset $
.
$\mathcal {A}^{h_{1}}\cap X=\emptyset $
.
7 Preprocessed conditions and outer hulls
In this section we introduce the notions of preprocessed conditions and outer hulls for the special case of
![]() $\kappa $
-Sacks forcing and its products. Note that both of these notions play a key role in Shelah’s proof of
$\kappa $
-Sacks forcing and its products. Note that both of these notions play a key role in Shelah’s proof of
![]() $\mathfrak {i}<\mathfrak {u}$
from [Reference Shelah22]: preprocessed conditions appear in [Reference Shelah22, Claim 1.11], while outer hulls appear in proof of [Reference Shelah22, Theorem 3.1] (page 440 of the article). Throughout this section we work under the assumption of GCH (at least
$\mathfrak {i}<\mathfrak {u}$
from [Reference Shelah22]: preprocessed conditions appear in [Reference Shelah22, Claim 1.11], while outer hulls appear in proof of [Reference Shelah22, Theorem 3.1] (page 440 of the article). Throughout this section we work under the assumption of GCH (at least
![]() $2^{\kappa }=\kappa ^{+}$
and
$2^{\kappa }=\kappa ^{+}$
and
![]() $2^{<\kappa }=\kappa $
) and
$2^{<\kappa }=\kappa $
) and
![]() $\kappa $
measurable. Thus in particular
$\kappa $
measurable. Thus in particular
![]() $\kappa $
is strongly inaccessible. We will work with the generalization of Sacks forcing and its products to the uncountable, both of which were first studied by Kanamori [Reference Kanamori19].
$\kappa $
is strongly inaccessible. We will work with the generalization of Sacks forcing and its products to the uncountable, both of which were first studied by Kanamori [Reference Kanamori19].
Recall that
![]() $p \subseteq 2^{< \kappa }$
is a tree if it is closed under initial segments. That is,
$p \subseteq 2^{< \kappa }$
is a tree if it is closed under initial segments. That is,
![]() $u \in p$
and
$u \in p$
and
![]() $v \subseteq u$
imply
$v \subseteq u$
imply
![]() $v \in p$
. Whenever p is a tree,
$v \in p$
. Whenever p is a tree,
![]() $t,r\in p$
, and t is a proper initial segment or equal to r, we write
$t,r\in p$
, and t is a proper initial segment or equal to r, we write
![]() $t\unlhd r$
and
$t\unlhd r$
and
![]() $r\unrhd t$
. A node
$r\unrhd t$
. A node
![]() $u\in p$
splits in p if both
$u\in p$
splits in p if both
![]() $u^{\frown } 0$
and
$u^{\frown } 0$
and
![]() $u^{\frown } 1$
belong to p. Given a tree p, we denote by
$u^{\frown } 1$
belong to p. Given a tree p, we denote by
![]() $\text {split}(p)$
the set of splitting nodes of p.
$\text {split}(p)$
the set of splitting nodes of p.
Definition 7.1. For a strongly inaccessible
![]() $\kappa $
, the
$\kappa $
, the
![]() $\kappa $
-Sacks forcing, denoted
$\kappa $
-Sacks forcing, denoted
![]() $\mathbb {S}_{\kappa }$
, is the poset consisting of sub-trees p of
$\mathbb {S}_{\kappa }$
, is the poset consisting of sub-trees p of
![]() $2^{<\kappa }$
such that:
$2^{<\kappa }$
such that:
-
(1) for each
 $u \in p$
there is
$u \in p$
there is
 $t \in p$
such that
$t \in p$
such that
 $u\unlhd t$
and t splits in p (t is said to be a splitting extension of u);
$u\unlhd t$
and t splits in p (t is said to be a splitting extension of u); -
(2) for any
 $\alpha < \kappa $
, if
$\alpha < \kappa $
, if
 $(u_{\beta }: \beta < \alpha )$
is a sequence of nodes in p such that
$(u_{\beta }: \beta < \alpha )$
is a sequence of nodes in p such that
 $\beta < \gamma < \alpha \to u_{\beta } \subseteq u_{\gamma }$
, then
$\beta < \gamma < \alpha \to u_{\beta } \subseteq u_{\gamma }$
, then
 $\bigcup \{u_{\beta }: \beta < \alpha \} \in p$
;
$\bigcup \{u_{\beta }: \beta < \alpha \} \in p$
; -
(3) if
 $\delta < \kappa $
is a limit ordinal,
$\delta < \kappa $
is a limit ordinal,
 $u \in 2^{\delta }$
, and for arbitrarily large
$u \in 2^{\delta }$
, and for arbitrarily large
 $\beta < \delta $
the node
$\beta < \delta $
the node
 $u \restriction \beta $
splits in p, then u splits in p.
$u \restriction \beta $
splits in p, then u splits in p.
The extension relation on
![]() $\mathbb {S}_{\kappa }$
is defined by
$\mathbb {S}_{\kappa }$
is defined by
![]() $p \leq q$
if and only if
$p \leq q$
if and only if
![]() $p \subseteq q$
.
$p \subseteq q$
.
As in the countable case we define the
![]() $\operatorname {\mathrm {stem}}(p)$
where p is a condition in
$\operatorname {\mathrm {stem}}(p)$
where p is a condition in
![]() $\mathbb {S}_{\kappa }$
as the unique splitting node that is comparable with all elements in p. By recursion on
$\mathbb {S}_{\kappa }$
as the unique splitting node that is comparable with all elements in p. By recursion on
![]() $\kappa $
define:
$\kappa $
define:
Definition 7.2 (The
 $\alpha $
-th splitting level of p).
$\alpha $
-th splitting level of p).
Given
![]() $p \in \mathbb {S}_{\kappa }$
let
$p \in \mathbb {S}_{\kappa }$
let
-
•
 $\operatorname {\mathrm {split}}_{0} (p) = \operatorname {\mathrm {stem}}(p)$
,
$\operatorname {\mathrm {split}}_{0} (p) = \operatorname {\mathrm {stem}}(p)$
, -
•
 $\operatorname {\mathrm {split}}_{\alpha +1}(p) = \{ \operatorname {\mathrm {stem}}(p_{u^{\frown } i}) : u \in \operatorname {\mathrm {split}}_{\alpha }(p)$
and
$\operatorname {\mathrm {split}}_{\alpha +1}(p) = \{ \operatorname {\mathrm {stem}}(p_{u^{\frown } i}) : u \in \operatorname {\mathrm {split}}_{\alpha }(p)$
and
 $i \in 2 \}$
,
$i \in 2 \}$
, -
• for
 $\delta <\kappa $
is a limit ordinal,
$\delta <\kappa $
is a limit ordinal,
 $\operatorname {\mathrm {split}}_{\delta }(p)= \{s \in p: s \text { is a limit of nodes in } \bigcup _{\alpha < \delta } \operatorname {\mathrm {split}}_{\alpha }(p)\} $
.
$\operatorname {\mathrm {split}}_{\delta }(p)= \{s \in p: s \text { is a limit of nodes in } \bigcup _{\alpha < \delta } \operatorname {\mathrm {split}}_{\alpha }(p)\} $
.
We refer to
![]() $\operatorname {\mathrm {split}}_{\alpha }(p)$
as the
$\operatorname {\mathrm {split}}_{\alpha }(p)$
as the
![]() $\alpha $
-th splitting level of p. Moreover for
$\alpha $
-th splitting level of p. Moreover for
![]() $t\in \text {split}(p)$
, let
$t\in \text {split}(p)$
, let
![]() $\operatorname {\mathrm {sl}}(t,p)= \alpha $
where
$\operatorname {\mathrm {sl}}(t,p)= \alpha $
where
![]() $t\in \text {split}_{\alpha }(p)$
.
$t\in \text {split}_{\alpha }(p)$
.
Using this splitting levels we define the fusion orderings
![]() $\leq _{\alpha }$
on
$\leq _{\alpha }$
on
![]() $\mathbb {S}_{\kappa }$
: Given q and p in
$\mathbb {S}_{\kappa }$
: Given q and p in
![]() $\mathbb {S}_{\kappa }$
let
$\mathbb {S}_{\kappa }$
let
![]() $q \leq _{\alpha } p$
if and only if
$q \leq _{\alpha } p$
if and only if
![]() $q \leq p$
and
$q \leq p$
and
![]() $\operatorname {\mathrm {split}}_{\alpha }(p)= \operatorname {\mathrm {split}}_{\alpha }(q)$
.
$\operatorname {\mathrm {split}}_{\alpha }(p)= \operatorname {\mathrm {split}}_{\alpha }(q)$
.
Definition 7.3. A fusion sequence
![]() $(p_{\alpha }: \alpha < \kappa ) \subseteq \mathbb {S}_{\kappa }$
is sequence of conditions in
$(p_{\alpha }: \alpha < \kappa ) \subseteq \mathbb {S}_{\kappa }$
is sequence of conditions in
![]() $\mathbb {S}_{\kappa }$
such that
$\mathbb {S}_{\kappa }$
such that
![]() $p_{\alpha +1} \leq _{\alpha } p_{\alpha }$
for all
$p_{\alpha +1} \leq _{\alpha } p_{\alpha }$
for all
![]() $\alpha <\kappa $
and whenever
$\alpha <\kappa $
and whenever
![]() $\delta < \kappa $
is a limit, then
$\delta < \kappa $
is a limit, then
![]() $p_{\delta } \leq _{\alpha } p_{\alpha }$
for all
$p_{\delta } \leq _{\alpha } p_{\alpha }$
for all
![]() $\alpha < \delta $
.
$\alpha < \delta $
.
For any regular uncountable cardinal
![]() $\lambda $
we denote by
$\lambda $
we denote by
![]() $\mathbb {S}^{\lambda }_{\kappa }$
the
$\mathbb {S}^{\lambda }_{\kappa }$
the
![]() $\kappa $
-support product of
$\kappa $
-support product of
![]() $\lambda $
many copies of
$\lambda $
many copies of
![]() $\mathbb {S}_{\kappa }$
. Moreover:
$\mathbb {S}_{\kappa }$
. Moreover:
Definition 7.4 (Product fusion, Definition 1.7 in [Reference Kanamori19]).
-
• If
 $(p_{\alpha }: \alpha < \beta ) \subseteq \mathbb {S}^{\lambda }_{\kappa }$
, we define a condition
$(p_{\alpha }: \alpha < \beta ) \subseteq \mathbb {S}^{\lambda }_{\kappa }$
, we define a condition
 $p = \bigwedge _{\alpha < \beta } p_{\alpha }$
with
$p = \bigwedge _{\alpha < \beta } p_{\alpha }$
with
 $\operatorname {\mathrm {dom}}(p) = \bigcup _{\alpha < \beta } \operatorname {\mathrm {dom}}(p_{\alpha })$
and for every
$\operatorname {\mathrm {dom}}(p) = \bigcup _{\alpha < \beta } \operatorname {\mathrm {dom}}(p_{\alpha })$
and for every
 $\gamma \in \operatorname {\mathrm {dom}}(p)$
,
$\gamma \in \operatorname {\mathrm {dom}}(p)$
,
 $p(\gamma )= \bigcap \{ p_{\alpha }(\gamma ): \gamma \in \operatorname {\mathrm {dom}}(p_{\alpha })\}$
. Note that in the case
$p(\gamma )= \bigcap \{ p_{\alpha }(\gamma ): \gamma \in \operatorname {\mathrm {dom}}(p_{\alpha })\}$
. Note that in the case
 $p \restriction \gamma \notin \mathbb {S}^{\gamma }_{\kappa }$
for
$p \restriction \gamma \notin \mathbb {S}^{\gamma }_{\kappa }$
for
 $\gamma \in \operatorname {\mathrm {dom}}(p)$
or
$\gamma \in \operatorname {\mathrm {dom}}(p)$
or
 $\lvert \operatorname {\mathrm {dom}}(p) \lvert> \kappa $
then p is left undefined.
$\lvert \operatorname {\mathrm {dom}}(p) \lvert> \kappa $
then p is left undefined. -
• If
 $p,q \in \mathbb {S}^{\lambda }_{\kappa }$
,
$p,q \in \mathbb {S}^{\lambda }_{\kappa }$
,
 $\alpha < \kappa $
and
$\alpha < \kappa $
and
 $F \subseteq \operatorname {\mathrm {dom}}(q)$
with
$F \subseteq \operatorname {\mathrm {dom}}(q)$
with
 $\lvert F \lvert \leq \kappa $
, we say
$\lvert F \lvert \leq \kappa $
, we say
 $p \leq _{F, \alpha } q$
if and only if
$p \leq _{F, \alpha } q$
if and only if
 $p \leq q$
and for every
$p \leq q$
and for every
 $\beta \in F$
,
$\beta \in F$
,
 $p(\beta ) \leq _{\alpha } q(\beta )$
.
$p(\beta ) \leq _{\alpha } q(\beta )$
.
Lemma 7.5 (Generalized fusion [Reference Kanamori19]).
Suppose
![]() $(p_{\alpha } : \alpha < \kappa )\subseteq \mathbb {S}^{\lambda }_{\kappa }$
and
$(p_{\alpha } : \alpha < \kappa )\subseteq \mathbb {S}^{\lambda }_{\kappa }$
and
![]() $ F_{\alpha } \subseteq \lambda $
have the following properties:
$ F_{\alpha } \subseteq \lambda $
have the following properties:
-
(1)
 $p_{\alpha +1} \leq _{F_{\alpha },\alpha } p_{\alpha }$
and
$p_{\alpha +1} \leq _{F_{\alpha },\alpha } p_{\alpha }$
and
 $p_{\delta } = \bigwedge _{\alpha < \delta } p_{\alpha }$
when
$p_{\delta } = \bigwedge _{\alpha < \delta } p_{\alpha }$
when
 $\delta $
is a limit ordinal
$\delta $
is a limit ordinal
 $< \!\kappa $
.
$< \!\kappa $
. -
(2)
 $\lvert F_{\alpha } \lvert < \kappa $
,
$\lvert F_{\alpha } \lvert < \kappa $
,
 $F_{\alpha } \subseteq F_{\alpha +1}$
,
$F_{\alpha } \subseteq F_{\alpha +1}$
,
 $F_{\delta } = \bigcup _{\alpha < \delta } F_{\alpha }$
for limit
$F_{\delta } = \bigcup _{\alpha < \delta } F_{\alpha }$
for limit
 $\delta < \kappa $
and
$\delta < \kappa $
and
 $\bigcup _{\alpha < \kappa } F_{\alpha } = \bigcup _{\alpha < \kappa } \operatorname {\mathrm {dom}}(p_{\alpha })$
.
$\bigcup _{\alpha < \kappa } F_{\alpha } = \bigcup _{\alpha < \kappa } \operatorname {\mathrm {dom}}(p_{\alpha })$
.
Then
![]() $p = \bigwedge _{\alpha < \kappa } p_{\alpha } \in \mathbb {S}^{\lambda }_{\kappa }$
and we refer to
$p = \bigwedge _{\alpha < \kappa } p_{\alpha } \in \mathbb {S}^{\lambda }_{\kappa }$
and we refer to
![]() $(p_{\alpha }, F_{\alpha } : \alpha < \kappa )$
as a generalized fusion sequence.
$(p_{\alpha }, F_{\alpha } : \alpha < \kappa )$
as a generalized fusion sequence.
In the following, we fix some notation:
Definition 7.6.
-
• Given a condition
 $p \in \mathbb {S}_{\kappa }^{\lambda }$
,
$p \in \mathbb {S}_{\kappa }^{\lambda }$
,
 $\alpha < \kappa $
and
$\alpha < \kappa $
and
 $F \subseteq \operatorname {\mathrm {supp}}(p)$
so that
$F \subseteq \operatorname {\mathrm {supp}}(p)$
so that
 $\lvert F \lvert < \kappa $
let
$\lvert F \lvert < \kappa $
let
 $\Lambda ^{F}_{\alpha }(p)=\prod _{i\in F}\operatorname {\mathrm {split}}_{\alpha }(p(i))$
. That is
$\Lambda ^{F}_{\alpha }(p)=\prod _{i\in F}\operatorname {\mathrm {split}}_{\alpha }(p(i))$
. That is  $$ \begin{align*}\Lambda^{F}_{\alpha}(p) = \{ \bar{\sigma} = (\sigma_{i})_{i \in F} : \sigma_{i} \in \operatorname{\mathrm{split}}_{\alpha}(p(i))\}.\end{align*} $$
$$ \begin{align*}\Lambda^{F}_{\alpha}(p) = \{ \bar{\sigma} = (\sigma_{i})_{i \in F} : \sigma_{i} \in \operatorname{\mathrm{split}}_{\alpha}(p(i))\}.\end{align*} $$
-
• For all
 $\bar {\sigma } \in \Lambda ^{F}_{\alpha }(p)$
let
$\bar {\sigma } \in \Lambda ^{F}_{\alpha }(p)$
let
 $p_{\bar {\sigma }}\leq p$
be defined as follows:
$p_{\bar {\sigma }}\leq p$
be defined as follows:
 $\operatorname {\mathrm {supp}}(p)=\operatorname {\mathrm {supp}}(p_{\bar {\sigma }})$
and
$\operatorname {\mathrm {supp}}(p)=\operatorname {\mathrm {supp}}(p_{\bar {\sigma }})$
and  $$ \begin{align*}p_{\bar{\sigma}}(i) = \begin{cases} (p(i))_{ \sigma_{i}}, & \text{if } i \in F, \\ p(i), & \text{otherwise. } \end{cases} \end{align*} $$
$$ \begin{align*}p_{\bar{\sigma}}(i) = \begin{cases} (p(i))_{ \sigma_{i}}, & \text{if } i \in F, \\ p(i), & \text{otherwise. } \end{cases} \end{align*} $$
-
• Given
 $h \in {^{F}2}$
and
$h \in {^{F}2}$
and
 $\bar {\sigma } \in \Lambda ^{F}_{\alpha }(p)$
, let
$\bar {\sigma } \in \Lambda ^{F}_{\alpha }(p)$
, let
 $p^{h}_{\bar {\sigma }}$
be defined as follows:
$p^{h}_{\bar {\sigma }}$
be defined as follows:
 $\operatorname {\mathrm {supp}}(p^{h}_{\bar {\sigma }})=\operatorname {\mathrm {supp}}(p)$
and
$\operatorname {\mathrm {supp}}(p^{h}_{\bar {\sigma }})=\operatorname {\mathrm {supp}}(p)$
and  $$ \begin{align*}p^{h}_{\bar{\sigma}}(i) = \begin{cases} (p(i))_{ \sigma_{i}^{\smallfrown} h(i)}, & \text{if } i \in F, \\ p(i), & \text{otherwise. } \end{cases} \end{align*} $$
$$ \begin{align*}p^{h}_{\bar{\sigma}}(i) = \begin{cases} (p(i))_{ \sigma_{i}^{\smallfrown} h(i)}, & \text{if } i \in F, \\ p(i), & \text{otherwise. } \end{cases} \end{align*} $$
7.1 Preprocessed conditions
The following notion of begin preprocessed for a condition can be seen for example in [Reference Shelah22, Lemma 1.11]. Given a name for a real
![]() $\tau $
and a condition p in an appropriate partial order, in particular the poset
$\tau $
and a condition p in an appropriate partial order, in particular the poset
![]() $Q_{\mathcal {I}}$
from [Reference Shelah22], Sacks forcing, or Miller partition forcing (see for definition for example [Reference Guzmán, Hrŭsák and Téllez17]), the notion provides a sufficiently good ground model approximation of
$Q_{\mathcal {I}}$
from [Reference Shelah22], Sacks forcing, or Miller partition forcing (see for definition for example [Reference Guzmán, Hrŭsák and Téllez17]), the notion provides a sufficiently good ground model approximation of
![]() $\tau $
realized by a condition q stronger than p.
$\tau $
realized by a condition q stronger than p.
We adapt the notion in the context of
![]() $\kappa $
-Sacks forcing and its products.
$\kappa $
-Sacks forcing and its products.
Definition 7.7.
-
(1) Let
 $\dot {X}$
be an
$\dot {X}$
be an
 $\mathbb {S}_{\kappa }$
-name for a subset of
$\mathbb {S}_{\kappa }$
-name for a subset of
 $\kappa $
. We say that
$\kappa $
. We say that
 $p\in \mathbb {S}_{\kappa }$
is preprocessed for
$p\in \mathbb {S}_{\kappa }$
is preprocessed for
 $\dot {X}$
if for all
$\dot {X}$
if for all
 $\alpha \in \kappa $
and all
$\alpha \in \kappa $
and all
 $t\in \operatorname {\mathrm {split}}_{\alpha }(p)$
there is
$t\in \operatorname {\mathrm {split}}_{\alpha }(p)$
there is
 $x_{t}\in {^{\alpha } 2}$
such that
$x_{t}\in {^{\alpha } 2}$
such that
 $p_{t}\Vdash \chi _{\dot {X}}\upharpoonright \alpha =\check {x}_{t}$
.
$p_{t}\Vdash \chi _{\dot {X}}\upharpoonright \alpha =\check {x}_{t}$
. -
(2)
-
(a) Let
 $\dot {X}$
be an
$\dot {X}$
be an
 $\mathbb {S}_{\kappa }^{\lambda }$
name for a subset of
$\mathbb {S}_{\kappa }^{\lambda }$
name for a subset of
 $\kappa $
,
$\kappa $
,
 $p \in \mathbb {S}_{\kappa }^{\lambda }$
and
$p \in \mathbb {S}_{\kappa }^{\lambda }$
and
 $F \subseteq \operatorname {\mathrm {supp}}(p)$
with
$F \subseteq \operatorname {\mathrm {supp}}(p)$
with
 $\lvert F \lvert < \kappa $
. We say that
$\lvert F \lvert < \kappa $
. We say that
 $p\in \mathbb {S}_{\kappa }^{\lambda }$
is preprocessed for the pair
$p\in \mathbb {S}_{\kappa }^{\lambda }$
is preprocessed for the pair
 $(F,\dot {X})$
if for all
$(F,\dot {X})$
if for all
 $\alpha <\kappa $
and all
$\alpha <\kappa $
and all
 $\bar {\sigma }\in \Lambda _{\alpha }^{F}(p)$
there are
$\bar {\sigma }\in \Lambda _{\alpha }^{F}(p)$
there are
 $F^{\prime } \supseteq F$
, such that
$F^{\prime } \supseteq F$
, such that
 $F^{\prime } \subseteq \operatorname {\mathrm {dom}}(p)$
and
$F^{\prime } \subseteq \operatorname {\mathrm {dom}}(p)$
and
 $\lvert F^{\prime }\lvert < \kappa $
,
$\lvert F^{\prime }\lvert < \kappa $
,
 $\bar {\tau }_{\bar {\sigma }} \in \Lambda _{\alpha }^{F^{\prime }}(p)$
, and
$\bar {\tau }_{\bar {\sigma }} \in \Lambda _{\alpha }^{F^{\prime }}(p)$
, and
 $x_{\bar {\sigma }}\in {^{\alpha } 2}$
such that
$x_{\bar {\sigma }}\in {^{\alpha } 2}$
such that
 $\bar {\sigma } \sqsubseteq \bar {\tau }_{\bar {\sigma }}$
and
$\bar {\sigma } \sqsubseteq \bar {\tau }_{\bar {\sigma }}$
and
 $p_{\bar {\tau }_{\bar {\sigma }}}\Vdash \chi _{\dot {X}}\upharpoonright \alpha =\check {x}_{\bar {\sigma }}$
.Footnote
7
$p_{\bar {\tau }_{\bar {\sigma }}}\Vdash \chi _{\dot {X}}\upharpoonright \alpha =\check {x}_{\bar {\sigma }}$
.Footnote
7
-
(b) We say that a condition
 $p \in \mathbb {S}_{\kappa }^{\lambda }$
is preprocessed for the name
$p \in \mathbb {S}_{\kappa }^{\lambda }$
is preprocessed for the name
 $\dot {X}$
if for all
$\dot {X}$
if for all
 $F \subseteq \operatorname {\mathrm {dom}}(p)$
such that
$F \subseteq \operatorname {\mathrm {dom}}(p)$
such that
 $\lvert F \lvert < \kappa $
, p is preprocessed for
$\lvert F \lvert < \kappa $
, p is preprocessed for
 $(\dot {X}, F)$
.
$(\dot {X}, F)$
.
-
Remark 7.8.
-
(1) Note that if
 $p\in \mathbb {S}_{\kappa }$
is preprocessed for
$p\in \mathbb {S}_{\kappa }$
is preprocessed for
 $\dot {X}$
, then for each
$\dot {X}$
, then for each
 $\alpha \in \kappa $
there is
$\alpha \in \kappa $
there is
 $Y_{\alpha }\subseteq {^{\alpha } 2}$
such that
$Y_{\alpha }\subseteq {^{\alpha } 2}$
such that
 $p\Vdash \chi _{\dot {X}}\upharpoonright \alpha \in \check {Y}_{\alpha }$
. Indeed, take
$p\Vdash \chi _{\dot {X}}\upharpoonright \alpha \in \check {Y}_{\alpha }$
. Indeed, take
 $Y_{\alpha } =\bigcup \{x_{t}:t\in \operatorname {\mathrm {split}}_{\alpha }(p)\}$
where
$Y_{\alpha } =\bigcup \{x_{t}:t\in \operatorname {\mathrm {split}}_{\alpha }(p)\}$
where
 $x_{t}$
is defined as in the definition above.
$x_{t}$
is defined as in the definition above. -
(2) Similarly, if
 $p\in \mathbb {S}_{\kappa }^{\lambda }$
is preprocessed for
$p\in \mathbb {S}_{\kappa }^{\lambda }$
is preprocessed for
 $(F,\dot {X})$
(F like above), then for each
$(F,\dot {X})$
(F like above), then for each
 $\alpha <\kappa $
there is
$\alpha <\kappa $
there is
 $Y_{\alpha }\subseteq {^{\alpha } 2}$
such that
$Y_{\alpha }\subseteq {^{\alpha } 2}$
such that
 $p\Vdash \chi _{\dot {X}}\upharpoonright \alpha \in \check {Y}_{\alpha }$
. Just take
$p\Vdash \chi _{\dot {X}}\upharpoonright \alpha \in \check {Y}_{\alpha }$
. Just take
 $Y_{\alpha } = \bigcup \{ x_{\bar {\sigma }}:\bar {\sigma }\in \Lambda ^{F}_{\alpha }(p) \}$
where
$Y_{\alpha } = \bigcup \{ x_{\bar {\sigma }}:\bar {\sigma }\in \Lambda ^{F}_{\alpha }(p) \}$
where
 $x_{\bar {\sigma }}$
is defined as above.
$x_{\bar {\sigma }}$
is defined as above.
Lemma 7.9.
-
(1) Let
 $p\in \mathbb {S}_{\kappa }$
and let
$p\in \mathbb {S}_{\kappa }$
and let
 $\dot {X}$
be an
$\dot {X}$
be an
 $\mathbb {S}_{\kappa }$
-name for a subset of
$\mathbb {S}_{\kappa }$
-name for a subset of
 $\kappa $
. Then there is
$\kappa $
. Then there is
 $q\leq p$
such that q is preprocessed for
$q\leq p$
such that q is preprocessed for
 $\dot {X}$
.
$\dot {X}$
. -
(2) Let
 $p\in \mathbb {S}_{\kappa }^{\lambda }$
and let
$p\in \mathbb {S}_{\kappa }^{\lambda }$
and let
 $\dot {X}$
be an
$\dot {X}$
be an
 $\mathbb {S}^{\lambda }_{\kappa }$
-name for a subset of
$\mathbb {S}^{\lambda }_{\kappa }$
-name for a subset of
 $\kappa $
. Then, for all
$\kappa $
. Then, for all
 $F \subseteq \operatorname {\mathrm {supp}}(p)$
with
$F \subseteq \operatorname {\mathrm {supp}}(p)$
with
 $\lvert F\lvert < \kappa $
and
$\lvert F\lvert < \kappa $
and
 $\gamma <\kappa $
there is
$\gamma <\kappa $
there is
 $q\leq _{F, \gamma } p$
such that q is preprocessed for
$q\leq _{F, \gamma } p$
such that q is preprocessed for
 $(F,\dot {X})$
.
$(F,\dot {X})$
.
Proof
![]() $(1)$
We build a fusion sequence
$(1)$
We build a fusion sequence
![]() $\langle q_{\alpha }:\alpha <\kappa \rangle $
below p such that for all
$\langle q_{\alpha }:\alpha <\kappa \rangle $
below p such that for all
![]() $\alpha>0$
and all
$\alpha>0$
and all
![]() $t\in \operatorname {\mathrm {split}}_{\alpha }(q_{\alpha })$
there is
$t\in \operatorname {\mathrm {split}}_{\alpha }(q_{\alpha })$
there is
![]() $x_{t}\in {^{\alpha } 2}$
such that
$x_{t}\in {^{\alpha } 2}$
such that
![]() $(q_{\alpha })_{t}\Vdash \chi _{\dot {X}}\upharpoonright \alpha =\check {x}_{t}$
. Start with
$(q_{\alpha })_{t}\Vdash \chi _{\dot {X}}\upharpoonright \alpha =\check {x}_{t}$
. Start with
![]() $q_{0}=p$
. Consider
$q_{0}=p$
. Consider
![]() $t\in \operatorname {\mathrm {split}}_{0}(p)$
, i.e.,
$t\in \operatorname {\mathrm {split}}_{0}(p)$
, i.e.,
![]() $t=\operatorname {\mathrm {stem}}(p)$
. For each
$t=\operatorname {\mathrm {stem}}(p)$
. For each
![]() $i\in \{0,1\}$
there is
$i\in \{0,1\}$
there is
![]() $w_{t,i}\leq p_{t^{\smallfrown } i}$
and
$w_{t,i}\leq p_{t^{\smallfrown } i}$
and
![]() $x(t,i)\in \{0,1\}$
such that
$x(t,i)\in \{0,1\}$
such that
![]() $w_{t,i}\Vdash \chi _{\dot {X}}(0)=\check {x}(t,i)$
. Note that
$w_{t,i}\Vdash \chi _{\dot {X}}(0)=\check {x}(t,i)$
. Note that
![]() $\text {stem}(w_{t,i})\unrhd \operatorname {\mathrm {stem}}(p_{t^{\smallfrown } i})\unrhd t^{\smallfrown } i$
. Define
$\text {stem}(w_{t,i})\unrhd \operatorname {\mathrm {stem}}(p_{t^{\smallfrown } i})\unrhd t^{\smallfrown } i$
. Define
![]() $q_{1}= w^{0}_{t,0}\cup w^{0}_{t,1}$
. Then
$q_{1}= w^{0}_{t,0}\cup w^{0}_{t,1}$
. Then
![]() $q_{1}\leq _{0} q_{0}$
and for all
$q_{1}\leq _{0} q_{0}$
and for all
![]() $s\in \operatorname {\mathrm {split}}_{1}(q_{1})$
there is
$s\in \operatorname {\mathrm {split}}_{1}(q_{1})$
there is
![]() $x_{s}\in {^{1}2}$
such that
$x_{s}\in {^{1}2}$
such that
![]() $(q_{1})_{s}\Vdash \chi _{\dot {X}}\upharpoonright 1=\check {x}_{s}$
. Indeed, if
$(q_{1})_{s}\Vdash \chi _{\dot {X}}\upharpoonright 1=\check {x}_{s}$
. Indeed, if
![]() $s\in \operatorname {\mathrm {split}}_{1}(q_{1})$
then
$s\in \operatorname {\mathrm {split}}_{1}(q_{1})$
then
![]() $s\unrhd t^{\smallfrown } i$
for
$s\unrhd t^{\smallfrown } i$
for
![]() $i\in \{0,1\}$
and so
$i\in \{0,1\}$
and so
![]() $(q_{1})_{s}=w_{t,i}$
. Thus
$(q_{1})_{s}=w_{t,i}$
. Thus
![]() $(q_{1})_{s}\Vdash \chi _{\dot {X}}\upharpoonright 1= x_{s}$
where
$(q_{1})_{s}\Vdash \chi _{\dot {X}}\upharpoonright 1= x_{s}$
where
![]() $x_{s}=(0,x(s,i))$
.
$x_{s}=(0,x(s,i))$
.
Now, suppose
![]() $q_{\alpha }$
has been defined and
$q_{\alpha }$
has been defined and
![]() $\forall t\in \operatorname {\mathrm {split}}_{\alpha }(q_{\alpha })$
there is
$\forall t\in \operatorname {\mathrm {split}}_{\alpha }(q_{\alpha })$
there is
![]() $x_{t}\in {^{\alpha } 2}$
such that
$x_{t}\in {^{\alpha } 2}$
such that
![]() $(q_{\alpha })_{t}\Vdash \chi _{\dot {X}}\upharpoonright \alpha =\check {x}_{t}$
. For each
$(q_{\alpha })_{t}\Vdash \chi _{\dot {X}}\upharpoonright \alpha =\check {x}_{t}$
. For each
![]() $t\in \operatorname {\mathrm {split}}_{\alpha }(q_{\alpha })$
and each
$t\in \operatorname {\mathrm {split}}_{\alpha }(q_{\alpha })$
and each
![]() $i\in \{0,1\}$
find
$i\in \{0,1\}$
find
![]() $w_{t,i}\leq (q_{\alpha })_{t^{\smallfrown } i}$
and
$w_{t,i}\leq (q_{\alpha })_{t^{\smallfrown } i}$
and
![]() $x(t,i)\in \{0,1\}$
such that
$x(t,i)\in \{0,1\}$
such that
![]() $w^{\alpha }_{t,i}\Vdash \chi _{\dot {X}}(\alpha )=\check {x}(t,i)$
. Then, take
$w^{\alpha }_{t,i}\Vdash \chi _{\dot {X}}(\alpha )=\check {x}(t,i)$
. Then, take
![]() $q_{\alpha +1}=\bigcup \{w_{t,i}: t\in \operatorname {\mathrm {split}}_{\alpha }(q_{\alpha }), i\in \{0,1\}\}$
. Then
$q_{\alpha +1}=\bigcup \{w_{t,i}: t\in \operatorname {\mathrm {split}}_{\alpha }(q_{\alpha }), i\in \{0,1\}\}$
. Then
![]() $\operatorname {\mathrm {split}}_{\alpha }(q_{\alpha +1})=\operatorname {\mathrm {split}}_{\alpha }(q_{\alpha })$
and so
$\operatorname {\mathrm {split}}_{\alpha }(q_{\alpha +1})=\operatorname {\mathrm {split}}_{\alpha }(q_{\alpha })$
and so
![]() $q_{\alpha +1}\leq _{\alpha } q_{\alpha }$
. Moreover, for all
$q_{\alpha +1}\leq _{\alpha } q_{\alpha }$
. Moreover, for all
![]() $t\in \operatorname {\mathrm {split}}_{\alpha +1}(q_{\alpha +1})$
there is
$t\in \operatorname {\mathrm {split}}_{\alpha +1}(q_{\alpha +1})$
there is
![]() $x_{t}\in {^{\alpha +1} 2}$
such that
$x_{t}\in {^{\alpha +1} 2}$
such that
![]() $(q_{\alpha +1})_{t}\Vdash \chi _{\dot {X}}\upharpoonright \alpha +1 =\check {x}_{t}$
. Indeed. Fix
$(q_{\alpha +1})_{t}\Vdash \chi _{\dot {X}}\upharpoonright \alpha +1 =\check {x}_{t}$
. Indeed. Fix
![]() $t\in \operatorname {\mathrm {split}}_{\alpha +1}(q_{\alpha +1})$
. Thus
$t\in \operatorname {\mathrm {split}}_{\alpha +1}(q_{\alpha +1})$
. Thus
![]() $r^{\smallfrown } i\unlhd t$
for some
$r^{\smallfrown } i\unlhd t$
for some
![]() $r\in \operatorname {\mathrm {split}}_{\alpha }(q_{\alpha +1})=\operatorname {\mathrm {split}}_{\alpha }(q_{\alpha })$
for some
$r\in \operatorname {\mathrm {split}}_{\alpha }(q_{\alpha +1})=\operatorname {\mathrm {split}}_{\alpha }(q_{\alpha })$
for some
![]() $i\in \{0,1\}$
. By Inductive Hypothesis
$i\in \{0,1\}$
. By Inductive Hypothesis
![]() $(q_{\alpha })_{r}\Vdash \chi _{\dot {X}}\upharpoonright \alpha =\check {x}_{r}$
for some
$(q_{\alpha })_{r}\Vdash \chi _{\dot {X}}\upharpoonright \alpha =\check {x}_{r}$
for some
![]() $x_{r}\in {^{\alpha } 2}$
. However
$x_{r}\in {^{\alpha } 2}$
. However
![]() $t\unrhd r^{\smallfrown } i$
and so
$t\unrhd r^{\smallfrown } i$
and so
![]() $(q_{\alpha +1})_{t}=w_{r,i}\leq (q_{\alpha })_{r^{\smallfrown } i}\leq (q_{\alpha })_{r}$
. Thus,
$(q_{\alpha +1})_{t}=w_{r,i}\leq (q_{\alpha })_{r^{\smallfrown } i}\leq (q_{\alpha })_{r}$
. Thus,
![]() $(q_{\alpha +1})_{t}\Vdash \chi _{\dot {X}}\upharpoonright \alpha =\check {x}_{r}\text { and }\chi _{\dot {X}}(\alpha )=\check {x}(r,i)$
. That is
$(q_{\alpha +1})_{t}\Vdash \chi _{\dot {X}}\upharpoonright \alpha =\check {x}_{r}\text { and }\chi _{\dot {X}}(\alpha )=\check {x}(r,i)$
. That is
![]() $(q_{\alpha +1})_{t}\Vdash \chi _{\dot {X}}\upharpoonright \alpha +1 =\check {x}_{t}$
where
$(q_{\alpha +1})_{t}\Vdash \chi _{\dot {X}}\upharpoonright \alpha +1 =\check {x}_{t}$
where
![]() $x_{t}=x_{r}\cup \{(\alpha , x(r,i))\}$
.
$x_{t}=x_{r}\cup \{(\alpha , x(r,i))\}$
.
It remains to consider the limit case. Suppose
![]() $\langle q_{\beta }:\beta <\alpha \rangle $
have been defined and for all
$\langle q_{\beta }:\beta <\alpha \rangle $
have been defined and for all
![]() $\beta <\alpha $
and all
$\beta <\alpha $
and all
![]() $t\in \operatorname {\mathrm {split}}_{\beta }(q_{\beta })$
there is
$t\in \operatorname {\mathrm {split}}_{\beta }(q_{\beta })$
there is
![]() $x_{t}\in {^{\beta } 2}$
such that
$x_{t}\in {^{\beta } 2}$
such that
![]() $(q_{\beta })_{t}\Vdash \chi _{\dot {X}}\upharpoonright \beta =\check {x}_{t}$
. Then take
$(q_{\beta })_{t}\Vdash \chi _{\dot {X}}\upharpoonright \beta =\check {x}_{t}$
. Then take
![]() $q_{\alpha }=\land _{\beta <\alpha } q_{\beta }$
. Note that if
$q_{\alpha }=\land _{\beta <\alpha } q_{\beta }$
. Note that if
![]() $t\in \operatorname {\mathrm {split}}_{\alpha }(q_{\alpha })$
then there is
$t\in \operatorname {\mathrm {split}}_{\alpha }(q_{\alpha })$
then there is
![]() $\{\eta _{\xi }:\xi <\alpha \}$
unbounded in
$\{\eta _{\xi }:\xi <\alpha \}$
unbounded in
![]() $\alpha $
such that
$\alpha $
such that
![]() $t\upharpoonright \eta _{\xi }\in \operatorname {\mathrm {split}}_{\xi }(q_{\xi })$
and so by inductive hypothesis for some
$t\upharpoonright \eta _{\xi }\in \operatorname {\mathrm {split}}_{\xi }(q_{\xi })$
and so by inductive hypothesis for some
![]() $x_{t\upharpoonright \eta _{\xi }}\in {^{\xi } 2}$
we have
$x_{t\upharpoonright \eta _{\xi }}\in {^{\xi } 2}$
we have
![]() $(q_{\xi })_{t\upharpoonright \eta _{\xi }}\Vdash \chi _{\dot {X}}\upharpoonright \xi =\check {x}_{t\upharpoonright \eta _{\xi }}$
. Then for
$(q_{\xi })_{t\upharpoonright \eta _{\xi }}\Vdash \chi _{\dot {X}}\upharpoonright \xi =\check {x}_{t\upharpoonright \eta _{\xi }}$
. Then for
![]() $x_{t}=\bigcup \{x_{t\upharpoonright \eta _{\xi }}:\xi <\alpha \}$
we have
$x_{t}=\bigcup \{x_{t\upharpoonright \eta _{\xi }}:\xi <\alpha \}$
we have
![]() $(q_{\alpha })_{t}\Vdash \chi _{\dot {X}}\upharpoonright \alpha =\check {x}_{t}$
.
$(q_{\alpha })_{t}\Vdash \chi _{\dot {X}}\upharpoonright \alpha =\check {x}_{t}$
.
![]() $(2)$
The argument for the product runs similarly as the above case: Let
$(2)$
The argument for the product runs similarly as the above case: Let
![]() $p \in \mathbb {S}_{\kappa }^{\lambda }$
,
$p \in \mathbb {S}_{\kappa }^{\lambda }$
,
![]() $\gamma < \kappa $
and
$\gamma < \kappa $
and
![]() $F \subseteq \operatorname {\mathrm {supp}}(p)$
so that
$F \subseteq \operatorname {\mathrm {supp}}(p)$
so that
![]() $\lvert F \lvert < \kappa $
. We shall define a fusion sequence
$\lvert F \lvert < \kappa $
. We shall define a fusion sequence
![]() $\langle q_{\alpha }, F_{\alpha }: \alpha <\kappa \rangle \subseteq \mathbb {S}_{\kappa }^{\lambda }$
below p, ordinals
$\langle q_{\alpha }, F_{\alpha }: \alpha <\kappa \rangle \subseteq \mathbb {S}_{\kappa }^{\lambda }$
below p, ordinals
![]() $(\eta _{\alpha }: \alpha < \kappa )$
and bijections
$(\eta _{\alpha }: \alpha < \kappa )$
and bijections
![]() $g_{\alpha }: F_{\alpha } \to \eta _{\alpha }$
such that for all
$g_{\alpha }: F_{\alpha } \to \eta _{\alpha }$
such that for all
![]() $\alpha <\kappa $
:
$\alpha <\kappa $
:
-
(1)
 $q_{\alpha +1} \leq _{F_{\alpha }, \gamma + \alpha } q_{\alpha }$
.
$q_{\alpha +1} \leq _{F_{\alpha }, \gamma + \alpha } q_{\alpha }$
. -
(2)
 $\eta _{\alpha } \geq \alpha $
.
$\eta _{\alpha } \geq \alpha $
. -
(3) For all
 $\alpha < \alpha ^{\prime }<\kappa $
,
$\alpha < \alpha ^{\prime }<\kappa $
,
 $g_{\alpha } \subseteq g_{\alpha ^{\prime }}$
and for limit ordinals
$g_{\alpha } \subseteq g_{\alpha ^{\prime }}$
and for limit ordinals
 $\delta < \kappa g_{\delta } = \bigcup _{\alpha < \delta } g_{\alpha }$
.
$\delta < \kappa g_{\delta } = \bigcup _{\alpha < \delta } g_{\alpha }$
. -
(4) For all
 ${\bar {\sigma }}\in \Lambda _{\gamma + \alpha }^{F_{\alpha }}(q_{\alpha }) $
there is
${\bar {\sigma }}\in \Lambda _{\gamma + \alpha }^{F_{\alpha }}(q_{\alpha }) $
there is
 $x_{\bar {\sigma }}\in {^{\alpha } 2}$
such that
$x_{\bar {\sigma }}\in {^{\alpha } 2}$
such that
 $(q_{\alpha +1})_{\bar {\sigma }}\Vdash \chi _{\dot {X}}\upharpoonright \alpha =\check {x}_{\bar {\sigma }}$
.
$(q_{\alpha +1})_{\bar {\sigma }}\Vdash \chi _{\dot {X}}\upharpoonright \alpha =\check {x}_{\bar {\sigma }}$
.
Since similar arguments will be used in the upcoming results we give the proof in full detail. Start with
![]() $q_{0} = p$
and
$q_{0} = p$
and
![]() $F_{0}= F$
, in order to arrange that
$F_{0}= F$
, in order to arrange that
![]() $q_{\alpha +1} \leq _{F_{\alpha }, \gamma + \alpha } q_{\alpha }$
start the following construction at some indecomposable ordinal
$q_{\alpha +1} \leq _{F_{\alpha }, \gamma + \alpha } q_{\alpha }$
start the following construction at some indecomposable ordinal
![]() $\alpha>\gamma $
(otherwise for all ordinals
$\alpha>\gamma $
(otherwise for all ordinals
![]() $\beta < \alpha $
,
$\beta < \alpha $
,
![]() $\beta +\alpha = \alpha $
and so, at
$\beta +\alpha = \alpha $
and so, at
![]() $\alpha $
we would just get
$\alpha $
we would just get
![]() $q_{\alpha +1} \leq _{F_{\alpha },\alpha } q_{\alpha }$
) and letting
$q_{\alpha +1} \leq _{F_{\alpha },\alpha } q_{\alpha }$
) and letting
![]() $q_{\beta } = p$
for all
$q_{\beta } = p$
for all
![]() $\beta <\alpha $
. At limit stages
$\beta <\alpha $
. At limit stages
![]() $\delta <\kappa $
the construction of
$\delta <\kappa $
the construction of
![]() $q_{\delta }$
and
$q_{\delta }$
and
![]() $F_{\delta }$
is determined by the conditions in Definition 7.4. Let
$F_{\delta }$
is determined by the conditions in Definition 7.4. Let
![]() $\eta _{\delta } = \sup _{\alpha <\delta } \eta _{\alpha }$
and
$\eta _{\delta } = \sup _{\alpha <\delta } \eta _{\alpha }$
and
![]() $g_{\delta }$
as above.
$g_{\delta }$
as above.
Finally for the successor case, suppose
![]() $q_{\alpha }$
,
$q_{\alpha }$
,
![]() $\eta _{\alpha }$
,
$\eta _{\alpha }$
,
![]() $g_{\alpha }$
, and
$g_{\alpha }$
, and
![]() $F_{\alpha }$
have been defined. Fix an enumeration
$F_{\alpha }$
have been defined. Fix an enumeration
![]() $\{\gamma _{l}=(\bar {\sigma }_{l}, h_{l}): l< \rho \}$
of all pairs of the form
$\{\gamma _{l}=(\bar {\sigma }_{l}, h_{l}): l< \rho \}$
of all pairs of the form
![]() $(\bar {\sigma }, h)$
such that
$(\bar {\sigma }, h)$
such that
![]() $\bar {\sigma } \in \Lambda _{\sigma }^{F_{\alpha }}(q_{\alpha })$
and
$\bar {\sigma } \in \Lambda _{\sigma }^{F_{\alpha }}(q_{\alpha })$
and
![]() $h \in {^{F_{\alpha }}2}$
. Note that the ordinals
$h \in {^{F_{\alpha }}2}$
. Note that the ordinals
![]() $\rho $
is
$\rho $
is
![]() $<\kappa $
.
$<\kappa $
.
Inductively, we will construct a sequence
![]() $\{r^{\alpha }_{l}:l<\rho \}$
of conditions below
$\{r^{\alpha }_{l}:l<\rho \}$
of conditions below
![]() $q_{\alpha }$
satisfying:
$q_{\alpha }$
satisfying:
-
(1)
 $r^{\alpha }_{0} = q_{\alpha }$
,
$r^{\alpha }_{0} = q_{\alpha }$
, -
(2)
 $r^{\alpha }_{l+1} \leq _{F_{\alpha },\gamma +\alpha } r^{\alpha }_{l}$
,
$r^{\alpha }_{l+1} \leq _{F_{\alpha },\gamma +\alpha } r^{\alpha }_{l}$
, -
(3)
 $(r^{\alpha }_{l+1})_{\bar {\sigma }_{l}}^{h_{l}}$
forces a value
$(r^{\alpha }_{l+1})_{\bar {\sigma }_{l}}^{h_{l}}$
forces a value
 $\check {x}(\alpha ,l)$
for
$\check {x}(\alpha ,l)$
for
 $\chi _{\dot {X}}\upharpoonright \alpha $
,
$\chi _{\dot {X}}\upharpoonright \alpha $
, -
(4) For l limit ordinal
 $r^{\alpha }_{l} = \bigwedge _{k< l} r^{\alpha }_{k}$
.
$r^{\alpha }_{l} = \bigwedge _{k< l} r^{\alpha }_{k}$
.
It is enough to explain how the successor step is built: Suppose that we have constructed
![]() $r^{\alpha }_{l}$
satisfying the conditions above and consider the pair
$r^{\alpha }_{l}$
satisfying the conditions above and consider the pair
![]() $\gamma _{l} =(\bar {\sigma }, h)$
, then find a condition
$\gamma _{l} =(\bar {\sigma }, h)$
, then find a condition
![]() $w_{l} \leq (r_{l})_{\bar {\sigma }}^{h}$
forcing a value
$w_{l} \leq (r_{l})_{\bar {\sigma }}^{h}$
forcing a value
![]() $x(\bar {\sigma },l)$
for
$x(\bar {\sigma },l)$
for
![]() $\chi _{\dot {X}}\upharpoonright \alpha $
. Note that
$\chi _{\dot {X}}\upharpoonright \alpha $
. Note that
![]() $w_{l}$
is clearly not a condition that satisfies (2), so we build
$w_{l}$
is clearly not a condition that satisfies (2), so we build
![]() $r^{\alpha }_{l+1}$
as follows:
$r^{\alpha }_{l+1}$
as follows:
![]() $\operatorname {\mathrm {supp}}(r^{\alpha }_{l+1})=\operatorname {\mathrm {supp}}(w_{l})$
and
$\operatorname {\mathrm {supp}}(r^{\alpha }_{l+1})=\operatorname {\mathrm {supp}}(w_{l})$
and
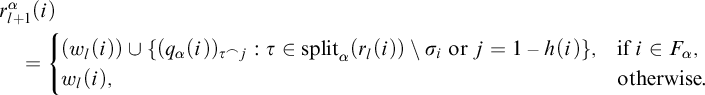 $$ \begin{align*}& r^{\alpha}_{l+1}(i)\\ &\quad = \begin{cases} (w_{l}(i)) \cup \{ (q_{\alpha}(i))_{\tau {}^{\frown} j}: \tau \in \operatorname{\mathrm{split}}_{\alpha} (r_{l}(i)) \setminus \sigma_{i} \text{ or } j= 1-h(i) \}, & \text{if } i \in F_{\alpha}, \\ w_{l}(i), & \text{otherwise. } \end{cases} \end{align*} $$
$$ \begin{align*}& r^{\alpha}_{l+1}(i)\\ &\quad = \begin{cases} (w_{l}(i)) \cup \{ (q_{\alpha}(i))_{\tau {}^{\frown} j}: \tau \in \operatorname{\mathrm{split}}_{\alpha} (r_{l}(i)) \setminus \sigma_{i} \text{ or } j= 1-h(i) \}, & \text{if } i \in F_{\alpha}, \\ w_{l}(i), & \text{otherwise. } \end{cases} \end{align*} $$
Note that this is now a condition satisfying the properties above. Put
![]() $q_{\alpha +1}= \bigwedge _{l< \rho } r^{\alpha }_{l} F_{\alpha +1}=F_{\alpha }\cup \{\min (\operatorname {\mathrm {supp}}(q_{\alpha +1})\backslash F_{\alpha })\}$
,
$q_{\alpha +1}= \bigwedge _{l< \rho } r^{\alpha }_{l} F_{\alpha +1}=F_{\alpha }\cup \{\min (\operatorname {\mathrm {supp}}(q_{\alpha +1})\backslash F_{\alpha })\}$
,
![]() $\eta _{\alpha +1} = \eta _{\alpha } +1$
, and
$\eta _{\alpha +1} = \eta _{\alpha } +1$
, and
![]() $g_{\alpha +1} = g_{\alpha } \cup \{(\min (\operatorname {\mathrm {supp}}(q_{\alpha +1})\backslash F_{\alpha }), \eta _{\alpha })\}$
.
$g_{\alpha +1} = g_{\alpha } \cup \{(\min (\operatorname {\mathrm {supp}}(q_{\alpha +1})\backslash F_{\alpha }), \eta _{\alpha })\}$
.
In order to finish the proof, we check that the condition q is indeed preprocessed for
![]() $(F, \dot {X})$
. Fix
$(F, \dot {X})$
. Fix
![]() $\alpha < \kappa $
and
$\alpha < \kappa $
and
![]() $\bar {\sigma } \in \Lambda _{\alpha }^{F}(q)$
. First, extend
$\bar {\sigma } \in \Lambda _{\alpha }^{F}(q)$
. First, extend
![]() $\bar {\sigma }$
to a sequence
$\bar {\sigma }$
to a sequence
![]() $\bar {\sigma }^{\prime }= \bar {\sigma }^{\frown } \bar {\rho }_{0}$
in
$\bar {\sigma }^{\prime }= \bar {\sigma }^{\frown } \bar {\rho }_{0}$
in
![]() $\Lambda _{\alpha }^{F_{\alpha }}(q)$
by adding a fix tail
$\Lambda _{\alpha }^{F_{\alpha }}(q)$
by adding a fix tail
![]() $\bar {\rho }_{0}$
of splitting nodes in
$\bar {\rho }_{0}$
of splitting nodes in
![]() $q(i)$
at level
$q(i)$
at level
![]() $\alpha $
for each
$\alpha $
for each
![]() $i \in F_{\alpha } \backslash F$
.
$i \in F_{\alpha } \backslash F$
.
Since
![]() $q \leq _{\alpha , F_{\alpha }} q_{\alpha }$
we get that
$q \leq _{\alpha , F_{\alpha }} q_{\alpha }$
we get that
![]() $\Lambda _{\alpha }^{F_{\alpha }}(q)= \Lambda _{\alpha }^{F_{\alpha }}(q_{\alpha })$
and so
$\Lambda _{\alpha }^{F_{\alpha }}(q)= \Lambda _{\alpha }^{F_{\alpha }}(q_{\alpha })$
and so
![]() $\bar {\sigma }^{\prime } \in \Lambda _{\alpha }^{F_{\alpha }}(q_{\alpha })$
and we can use the fusion properties to get that there is an
$\bar {\sigma }^{\prime } \in \Lambda _{\alpha }^{F_{\alpha }}(q_{\alpha })$
and we can use the fusion properties to get that there is an
![]() $x_{\bar {\sigma }^{\prime }} \in {^{\alpha } 2}$
such that
$x_{\bar {\sigma }^{\prime }} \in {^{\alpha } 2}$
such that
![]() $(q_{\alpha +1})_{\bar {\sigma }^{\prime }} \Vdash \chi _{\dot {X}}\upharpoonright (\alpha ) = \check {x}_{\bar {\sigma }^{\prime }}$
, so we finally use that the condition
$(q_{\alpha +1})_{\bar {\sigma }^{\prime }} \Vdash \chi _{\dot {X}}\upharpoonright (\alpha ) = \check {x}_{\bar {\sigma }^{\prime }}$
, so we finally use that the condition
![]() $q_{\bar {\sigma }^{\prime }} \leq (q_{\alpha +1})_{\bar {\sigma }^{\prime }}$
to get that
$q_{\bar {\sigma }^{\prime }} \leq (q_{\alpha +1})_{\bar {\sigma }^{\prime }}$
to get that
![]() $(q)_{\bar {\sigma }^{\prime }} \Vdash \chi _{\dot {X}}\upharpoonright (\alpha ) = \check {x}_{\bar {\sigma }^{\prime }}$
as we wanted.
$(q)_{\bar {\sigma }^{\prime }} \Vdash \chi _{\dot {X}}\upharpoonright (\alpha ) = \check {x}_{\bar {\sigma }^{\prime }}$
as we wanted.
Corollary 7.10. Let
![]() $p\in \mathbb {S}_{\kappa }^{\lambda }$
and let
$p\in \mathbb {S}_{\kappa }^{\lambda }$
and let
![]() $\dot {X}$
be an
$\dot {X}$
be an
![]() $\mathbb {S}^{\lambda }_{\kappa }$
-name for a subset of
$\mathbb {S}^{\lambda }_{\kappa }$
-name for a subset of
![]() $\kappa $
, then we can find
$\kappa $
, then we can find
![]() $q \leq p$
such that q is preprocessed for
$q \leq p$
such that q is preprocessed for
![]() $\dot {X}$
.
$\dot {X}$
.
Proof Recall first that there are
![]() $\kappa $
-many sets
$\kappa $
-many sets
![]() $G \subseteq \operatorname {\mathrm {dom}}(p)$
so that
$G \subseteq \operatorname {\mathrm {dom}}(p)$
so that
![]() $\lvert G \lvert < \kappa $
, so let
$\lvert G \lvert < \kappa $
, so let
![]() $(G_{\beta }: \beta <\kappa )$
be an enumeration of them. We can use build a fusion sequence
$(G_{\beta }: \beta <\kappa )$
be an enumeration of them. We can use build a fusion sequence
![]() $(q_{\alpha }, F_{\alpha })$
below p such that for all
$(q_{\alpha }, F_{\alpha })$
below p such that for all
![]() $\alpha < \kappa $
,
$\alpha < \kappa $
,
![]() $q_{\alpha + 1}$
is preprocessed for
$q_{\alpha + 1}$
is preprocessed for
![]() $(\dot {X}, G_{\alpha })$
.
$(\dot {X}, G_{\alpha })$
.
Start with
![]() $q_{0} = p$
and
$q_{0} = p$
and
![]() $F_{0} = G_{0}$
. The limit step is built as usual and it is left to explain how the successor case is constructed: Suppose we have already defined
$F_{0} = G_{0}$
. The limit step is built as usual and it is left to explain how the successor case is constructed: Suppose we have already defined
![]() $q_{\alpha }$
and
$q_{\alpha }$
and
![]() $F_{\alpha }$
, then we use the lemma above for
$F_{\alpha }$
, then we use the lemma above for
![]() $\dot {X}$
,
$\dot {X}$
,
![]() $q_{\alpha }$
, and
$q_{\alpha }$
, and
![]() $F_{\alpha }$
to get a condition
$F_{\alpha }$
to get a condition
![]() $r \leq _{\alpha , F_{\alpha }} q_{\alpha }$
that is preprocessed for
$r \leq _{\alpha , F_{\alpha }} q_{\alpha }$
that is preprocessed for
![]() $(\dot {X}, G_{\alpha })$
. Define then
$(\dot {X}, G_{\alpha })$
. Define then
![]() $q_{\alpha +1} =r$
and
$q_{\alpha +1} =r$
and
![]() $F_{\alpha +1} = F_{\alpha } \cup G_{\alpha }$
.
$F_{\alpha +1} = F_{\alpha } \cup G_{\alpha }$
.
We claim that the fusion q of the sequence defined above is preprocessed for all
![]() $G_{\alpha }$
’s: Indeed, if
$G_{\alpha }$
’s: Indeed, if
![]() $\alpha $
is fixed we know that
$\alpha $
is fixed we know that
![]() $q_{\alpha +1}$
is preprocessed for
$q_{\alpha +1}$
is preprocessed for
![]() $(\dot {X}, G_{\alpha })$
, then it is enough to notice that since
$(\dot {X}, G_{\alpha })$
, then it is enough to notice that since
![]() $q \leq _{\alpha +1, F_{\alpha +1}} q_{\alpha +1}$
, then q is also preprocessed for
$q \leq _{\alpha +1, F_{\alpha +1}} q_{\alpha +1}$
, then q is also preprocessed for
![]() $(\dot {X}, G_{\alpha })$
.
$(\dot {X}, G_{\alpha })$
.
7.2 Outer hull
Below, we introduce the notion of an outer hull, making explicit some well-known techniques. In the consistency proof of
![]() $\mathfrak {i}<\mathfrak {u}$
from [Reference Shelah22], outer hulls appear on page 440. Other more recent applications of the notion can be found for example in [Reference Guzmán, Hrŭsák and Téllez17].
$\mathfrak {i}<\mathfrak {u}$
from [Reference Shelah22], outer hulls appear on page 440. Other more recent applications of the notion can be found for example in [Reference Guzmán, Hrŭsák and Téllez17].
Definition 7.11.
-
• Let
 $p\in \mathbb {S}_{\kappa }$
and let
$p\in \mathbb {S}_{\kappa }$
and let
 $\dot {X}$
be an
$\dot {X}$
be an
 $\mathbb {S}_{\kappa }$
-name for a subset of
$\mathbb {S}_{\kappa }$
-name for a subset of
 $\kappa $
. For each
$\kappa $
. For each
 $t\in \text {split}_{\alpha }(p)$
, we refer to the set
$t\in \text {split}_{\alpha }(p)$
, we refer to the set
 $Y_{t}=\{\beta \in \kappa : p_{t}\not \Vdash \check {\beta }\notin \dot {X}\}$
, as the outer hull of
$Y_{t}=\{\beta \in \kappa : p_{t}\not \Vdash \check {\beta }\notin \dot {X}\}$
, as the outer hull of
 $\dot {X}$
below
$\dot {X}$
below
 $p_{t}$
. Moreover, if
$p_{t}$
. Moreover, if
 $q_{t,\beta }\leq p_{t}$
and
$q_{t,\beta }\leq p_{t}$
and
 $q_{t,\beta }\Vdash \check {\beta }\in \dot {X}$
, we say that
$q_{t,\beta }\Vdash \check {\beta }\in \dot {X}$
, we say that
 $q_{t,\beta }$
is a witness for
$q_{t,\beta }$
is a witness for
 $\beta \in Y_{t}$
.
$\beta \in Y_{t}$
. -
• Let
 $p\in \mathbb {S}^{\lambda }_{\kappa }$
and let
$p\in \mathbb {S}^{\lambda }_{\kappa }$
and let
 $\dot {X}$
be an
$\dot {X}$
be an
 $\mathbb {S}^{\lambda }_{\kappa }$
-name for a subset of
$\mathbb {S}^{\lambda }_{\kappa }$
-name for a subset of
 $\kappa $
. For all
$\kappa $
. For all
 $\alpha < \kappa $
,
$\alpha < \kappa $
,
 $F \subseteq \operatorname {\mathrm {supp}}(p)$
such that
$F \subseteq \operatorname {\mathrm {supp}}(p)$
such that
 $\lvert F \lvert < \kappa $
and
$\lvert F \lvert < \kappa $
and
 $\bar {\sigma } \in \Lambda ^{F}_{\alpha }(p)$
we refer to the set
$\bar {\sigma } \in \Lambda ^{F}_{\alpha }(p)$
we refer to the set
 $Y_{\bar {\sigma }}=\{\beta \in \kappa : p_{\bar {\sigma }}\not \Vdash \check {\beta }\notin \dot {X}\}$
, as the outer hull of
$Y_{\bar {\sigma }}=\{\beta \in \kappa : p_{\bar {\sigma }}\not \Vdash \check {\beta }\notin \dot {X}\}$
, as the outer hull of
 $\dot {X}$
below
$\dot {X}$
below
 $p_{\bar {\sigma }}$
. Moreover, if
$p_{\bar {\sigma }}$
. Moreover, if
 $q_{\bar {\sigma },\beta }\leq p_{\bar {\sigma }}$
and
$q_{\bar {\sigma },\beta }\leq p_{\bar {\sigma }}$
and
 $q_{\bar {\sigma },\beta }\Vdash \check {\beta }\in \dot {X}$
, we say that
$q_{\bar {\sigma },\beta }\Vdash \check {\beta }\in \dot {X}$
, we say that
 $q_{\bar {\sigma },\beta }$
is a witness for
$q_{\bar {\sigma },\beta }$
is a witness for
 $\beta \in Y_{\bar {\sigma }}$
.
$\beta \in Y_{\bar {\sigma }}$
.
Remark 7.12. Let
![]() $\dot {X}$
be an
$\dot {X}$
be an
![]() $\mathbb {S}_{\kappa }$
-name for a subset of
$\mathbb {S}_{\kappa }$
-name for a subset of
![]() $\kappa $
. Suppose
$\kappa $
. Suppose
![]() $Y_{t}$
is the outer hull of
$Y_{t}$
is the outer hull of
![]() $\dot {X}$
below
$\dot {X}$
below
![]() $p_{t}$
. If
$p_{t}$
. If
![]() $p_{t}\Vdash \check {\beta }\in \dot {X}$
, then
$p_{t}\Vdash \check {\beta }\in \dot {X}$
, then
![]() $p_{t}$
is a witness to
$p_{t}$
is a witness to
![]() $\beta \in Y_{t}$
and so
$\beta \in Y_{t}$
and so
![]() $p_{t}\Vdash \dot {X}\subseteq \check {Y}_{t}$
. Analogously for
$p_{t}\Vdash \dot {X}\subseteq \check {Y}_{t}$
. Analogously for
![]() $\mathbb {S}^{\lambda }_{\kappa }$
and
$\mathbb {S}^{\lambda }_{\kappa }$
and
![]() $Y_{\bar {\sigma }}$
.
$Y_{\bar {\sigma }}$
.
We proceed with the following lemma.
Lemma 7.13.
-
(1) Let
 $p\in \mathbb {S}_{\kappa }$
be preprocessed for
$p\in \mathbb {S}_{\kappa }$
be preprocessed for
 $\dot {X}$
and for each
$\dot {X}$
and for each
 $t\in \operatorname {\mathrm {split}}(p)$
let
$t\in \operatorname {\mathrm {split}}(p)$
let
 $Y_{t}$
be the outer hull of
$Y_{t}$
be the outer hull of
 $\dot {X}$
below
$\dot {X}$
below
 $p_{t}$
. Then for each
$p_{t}$
. Then for each
 $\alpha < \kappa $
,
$\alpha < \kappa $
,
 $t\in \text {split}_{\alpha }(p)$
and
$t\in \text {split}_{\alpha }(p)$
and
 $\beta \in Y_{t}$
there is an
$\beta \in Y_{t}$
there is an
 $r(t,\beta )\in p$
such that t is an initial segment of
$r(t,\beta )\in p$
such that t is an initial segment of
 $r(t,\beta )$
and
$r(t,\beta )$
and
 $p_{r(t,\beta )}\Vdash \check {\beta }\in \dot {X}$
. Moreover, for each
$p_{r(t,\beta )}\Vdash \check {\beta }\in \dot {X}$
. Moreover, for each
 $t\in \text {split}(p)$
and each
$t\in \text {split}(p)$
and each
 $\beta \in Y_{t}$
there is
$\beta \in Y_{t}$
there is
 $r=r(t,\beta )\in \text {split}_{\beta }(p)$
such that
$r=r(t,\beta )\in \text {split}_{\beta }(p)$
such that
 $p_{r}\Vdash \check {\beta }\in \dot {X}$
.
$p_{r}\Vdash \check {\beta }\in \dot {X}$
. -
(2) Let
 $p\in \mathbb {S}^{\lambda }_{\kappa }$
be preprocessed for
$p\in \mathbb {S}^{\lambda }_{\kappa }$
be preprocessed for
 $(\dot {X}, F)$
(where
$(\dot {X}, F)$
(where
 $F \subseteq \operatorname {\mathrm {supp}}(p)$
and
$F \subseteq \operatorname {\mathrm {supp}}(p)$
and
 $\lvert F\lvert < \kappa $
) and for each
$\lvert F\lvert < \kappa $
) and for each
 $\bar {\sigma } \in \Lambda ^{F}_{\alpha }(p)$
let
$\bar {\sigma } \in \Lambda ^{F}_{\alpha }(p)$
let
 $Y_{\bar {\sigma }}$
be the outer hull of
$Y_{\bar {\sigma }}$
be the outer hull of
 $\dot {X}$
below
$\dot {X}$
below
 $p_{\bar {\sigma }}$
. Then for each
$p_{\bar {\sigma }}$
. Then for each
 $\alpha < \kappa $
,
$\alpha < \kappa $
,
 $\bar {\sigma } \in \Lambda ^{F}_{\alpha }(p)$
,
$\bar {\sigma } \in \Lambda ^{F}_{\alpha }(p)$
,
 $\beta \in Y_{\bar {\sigma }}$
, and
$\beta \in Y_{\bar {\sigma }}$
, and
 $i \in F$
there are
$i \in F$
there are
 $F^{\prime } \supseteq F$
,
$F^{\prime } \supseteq F$
,
 $\lvert F^{\prime } \lvert <\kappa $
, and
$\lvert F^{\prime } \lvert <\kappa $
, and
 $\bar {\tau }^{\prime } \in \Lambda _{\alpha }^{F^{\prime }}(p)$
such that if
$\bar {\tau }^{\prime } \in \Lambda _{\alpha }^{F^{\prime }}(p)$
such that if
 $\bar {\tau }^{\prime }=(r_{i}(\bar {\sigma }, \beta ) : i \in F^{\prime })$
then
$\bar {\tau }^{\prime }=(r_{i}(\bar {\sigma }, \beta ) : i \in F^{\prime })$
then
 $r_{i}(\bar {\sigma },\beta )\in p(i)$
such that
$r_{i}(\bar {\sigma },\beta )\in p(i)$
such that
 $\sigma _{i}$
is an initial segment of
$\sigma _{i}$
is an initial segment of
 $r_{i}(\bar {\sigma },\beta )$
for all
$r_{i}(\bar {\sigma },\beta )$
for all
 $i \in F$
and
$i \in F$
and
 $p_{\bar {\tau }^{\prime }}\Vdash \check {\beta }\in \dot {X}$
. Moreover, for each
$p_{\bar {\tau }^{\prime }}\Vdash \check {\beta }\in \dot {X}$
. Moreover, for each
 $\bar {\sigma } \in \Lambda ^{F}_{\alpha }(p)$
,
$\bar {\sigma } \in \Lambda ^{F}_{\alpha }(p)$
,
 $\beta \in Y_{\bar {\sigma }}$
, and
$\beta \in Y_{\bar {\sigma }}$
, and
 $i \in F$
there are
$i \in F$
there are
 $F^{\prime } \supseteq F$
,
$F^{\prime } \supseteq F$
,
 $\lvert F^{\prime } \lvert <\kappa $
, and
$\lvert F^{\prime } \lvert <\kappa $
, and
 $\bar {\tau }^{\prime } \in \Lambda _{\alpha }^{F^{\prime }}(p)$
such that if
$\bar {\tau }^{\prime } \in \Lambda _{\alpha }^{F^{\prime }}(p)$
such that if
 $\bar {\tau }=(r_{i}(\bar {\sigma }, \beta ) : i \in F^{\prime })$
where
$\bar {\tau }=(r_{i}(\bar {\sigma }, \beta ) : i \in F^{\prime })$
where
 $r_{i}=r_{i}(\bar {\sigma },\beta )\in \text {split}_{\beta }(p)(i)$
for all
$r_{i}=r_{i}(\bar {\sigma },\beta )\in \text {split}_{\beta }(p)(i)$
for all
 $i\in F$
, then
$i\in F$
, then
 $p_{\bar {\tau }^{\prime }}\Vdash \check {\beta }\in \dot {X}$
.
$p_{\bar {\tau }^{\prime }}\Vdash \check {\beta }\in \dot {X}$
.
Proof
![]() $(1)$
Fix
$(1)$
Fix
![]() $\alpha ,t$
and
$\alpha ,t$
and
![]() $\beta \in Y_{t}$
. Then there is
$\beta \in Y_{t}$
. Then there is
![]() $q \leq p_{t}$
such that
$q \leq p_{t}$
such that
![]() $q\Vdash \beta \in \dot {X}$
. Take any
$q\Vdash \beta \in \dot {X}$
. Take any
![]() $r= r(t, \beta )\in \text {split}_{\beta }(q)$
. Note that
$r= r(t, \beta )\in \text {split}_{\beta }(q)$
. Note that
![]() $t\unlhd r$
and there is
$t\unlhd r$
and there is
![]() $\beta ^{\prime }\geq \beta $
such that
$\beta ^{\prime }\geq \beta $
such that
![]() $r\in \text {split}_{\beta ^{\prime }}(p)$
. On the other hand, because p is preprocessed we can use Lemma 7.9 to find
$r\in \text {split}_{\beta ^{\prime }}(p)$
. On the other hand, because p is preprocessed we can use Lemma 7.9 to find
![]() $x_{r} \subseteq {^{\alpha ^{\prime }} 2}$
such that
$x_{r} \subseteq {^{\alpha ^{\prime }} 2}$
such that
![]() $p_{r}\Vdash \chi _{\dot {X}} \upharpoonright \beta ^{\prime } = \check {x}_{r}$
. Since
$p_{r}\Vdash \chi _{\dot {X}} \upharpoonright \beta ^{\prime } = \check {x}_{r}$
. Since
![]() $q_{r}\leq p_{r}$
we must have that
$q_{r}\leq p_{r}$
we must have that
![]() $ \check {x}_{t}(\beta )=1$
. Thus
$ \check {x}_{t}(\beta )=1$
. Thus
![]() $p_{r}\Vdash \beta \in \dot {X}$
.
$p_{r}\Vdash \beta \in \dot {X}$
.
Moreover, if
![]() $r^{*}\unlhd r$
and
$r^{*}\unlhd r$
and
![]() $r^{*}\in \text {split}_{\beta +1}(p)$
then already
$r^{*}\in \text {split}_{\beta +1}(p)$
then already
![]() $p_{r^{*}}\Vdash \check {\beta }\in \dot {X}$
. Indeed, since p is preprocessed there is an
$p_{r^{*}}\Vdash \check {\beta }\in \dot {X}$
. Indeed, since p is preprocessed there is an
![]() $x_{r^{*}} \in {^{\beta } 2}$
so that
$x_{r^{*}} \in {^{\beta } 2}$
so that
![]() $p_{r^{*}} \Vdash \chi _{\dot {X}} \upharpoonright _{\beta +1} \in \check {x}_{r^{*}}$
, thus
$p_{r^{*}} \Vdash \chi _{\dot {X}} \upharpoonright _{\beta +1} \in \check {x}_{r^{*}}$
, thus
![]() $p_{r}$
forces a value for
$p_{r}$
forces a value for
![]() $\chi _{\dot {X}}(\beta )$
which has to be 1 because
$\chi _{\dot {X}}(\beta )$
which has to be 1 because
![]() $q_{r} \leq q,p_{r}$
and so
$q_{r} \leq q,p_{r}$
and so
![]() $p_{r} \Vdash \check {\beta } \in \dot {X}$
. In particular, if
$p_{r} \Vdash \check {\beta } \in \dot {X}$
. In particular, if
![]() $\beta \leq \operatorname {\mathrm {sl}}(t,p)$
then in fact
$\beta \leq \operatorname {\mathrm {sl}}(t,p)$
then in fact
![]() $p_{t}\Vdash \check {\beta }\in \dot {X}$
.
$p_{t}\Vdash \check {\beta }\in \dot {X}$
.
![]() $(2)$
In the same way, fix now
$(2)$
In the same way, fix now
![]() $\alpha , F$
and
$\alpha , F$
and
![]() $\bar {\sigma } \in \Lambda _{\alpha }^{F}(p)$
. Then there is
$\bar {\sigma } \in \Lambda _{\alpha }^{F}(p)$
. Then there is
![]() $q \leq p_{\bar {\sigma }}$
such that
$q \leq p_{\bar {\sigma }}$
such that
![]() $q\Vdash \beta \in \dot {X}$
. For all
$q\Vdash \beta \in \dot {X}$
. For all
![]() $i \in F$
take any
$i \in F$
take any
![]() $r_{i}= r_{i}(\bar {\sigma }, \beta )\in \text {split}_{\beta }(q(i))$
. Note that
$r_{i}= r_{i}(\bar {\sigma }, \beta )\in \text {split}_{\beta }(q(i))$
. Note that
![]() $\sigma _{i}\unlhd r_{i}$
for all
$\sigma _{i}\unlhd r_{i}$
for all
![]() $i \in F$
. We can find
$i \in F$
. We can find
![]() $\beta ^{\prime }\geq \beta $
such that
$\beta ^{\prime }\geq \beta $
such that
![]() $r_{i} \in \text {split}_{\beta ^{\prime }}(p(i))$
uniformly for all
$r_{i} \in \text {split}_{\beta ^{\prime }}(p(i))$
uniformly for all
![]() $i \in F$
. Hence if
$i \in F$
. Hence if
![]() $\bar {\tau }=(r_{i}(\bar {\sigma }, \beta ) : i \in F)$
, by Lemma 7.9 there are
$\bar {\tau }=(r_{i}(\bar {\sigma }, \beta ) : i \in F)$
, by Lemma 7.9 there are
![]() $F^{\prime } \supseteq F$
,
$F^{\prime } \supseteq F$
,
![]() $\bar {\tau }^{\prime } \in \Lambda _{\alpha }^{F^{\prime }}(p)$
, and
$\bar {\tau }^{\prime } \in \Lambda _{\alpha }^{F^{\prime }}(p)$
, and
![]() $x_{\bar {\tau }^{\prime }} \in {^{\beta ^{\prime }} 2}$
such that
$x_{\bar {\tau }^{\prime }} \in {^{\beta ^{\prime }} 2}$
such that
![]() $p_{\bar {\tau }^{\prime }}\Vdash \chi _{\dot {X}} \upharpoonright \beta ^{\prime } = \check {x}_{\bar {\tau }}$
. Let
$p_{\bar {\tau }^{\prime }}\Vdash \chi _{\dot {X}} \upharpoonright \beta ^{\prime } = \check {x}_{\bar {\tau }}$
. Let
![]() $y= \chi _{\dot {X}} \upharpoonright \beta ^{\prime }$
. Since
$y= \chi _{\dot {X}} \upharpoonright \beta ^{\prime }$
. Since
![]() $q_{\bar {\tau }^{\prime }}\leq p_{\bar {\tau }^{\prime }}$
we must have that
$q_{\bar {\tau }^{\prime }}\leq p_{\bar {\tau }^{\prime }}$
we must have that
![]() $ y(\beta )=1$
. Thus
$ y(\beta )=1$
. Thus
![]() $p_{\bar {\tau }^{\prime }}\Vdash \beta \in \dot {X}$
. The argument for the moreover part is the same as for part (1).
$p_{\bar {\tau }^{\prime }}\Vdash \beta \in \dot {X}$
. The argument for the moreover part is the same as for part (1).
Definition 7.14. For
![]() $p\in \mathbb {S}_{\kappa }^{\lambda }$
and
$p\in \mathbb {S}_{\kappa }^{\lambda }$
and
![]() $F\in [\text {supp}(p)]^{<\kappa }$
, let
$F\in [\text {supp}(p)]^{<\kappa }$
, let
![]() $\Lambda (F)=\bigcup _{\alpha <\kappa }\Lambda ^{F}_{\alpha }$
. For
$\Lambda (F)=\bigcup _{\alpha <\kappa }\Lambda ^{F}_{\alpha }$
. For
![]() $\bar {\sigma }$
and
$\bar {\sigma }$
and
![]() $\bar {\tau }$
in
$\bar {\tau }$
in
![]() $\Lambda (F)$
we say that
$\Lambda (F)$
we say that
![]() $\bar {\tau }\unlhd \bar {\sigma }$
if and only if for each
$\bar {\tau }\unlhd \bar {\sigma }$
if and only if for each
![]() $i\in F(\bar {\tau }(i)\unlhd \bar {\sigma }(i))$
.
$i\in F(\bar {\tau }(i)\unlhd \bar {\sigma }(i))$
.
Corollary 7.15.
-
(1) Let
 $\dot {X}$
be an
$\dot {X}$
be an
 $\mathbb {S}_{\kappa }$
-name for an infinite subset of
$\mathbb {S}_{\kappa }$
-name for an infinite subset of
 $\kappa $
. If
$\kappa $
. If
 $p\in \mathbb {S}_{\kappa }$
is preprocessed for
$p\in \mathbb {S}_{\kappa }$
is preprocessed for
 $\dot {X}$
,
$\dot {X}$
,
 $t\in \operatorname {\mathrm {split}}(p)$
, and
$t\in \operatorname {\mathrm {split}}(p)$
, and
 $Y_{t}$
is the outer hull of
$Y_{t}$
is the outer hull of
 $\dot {X}$
below
$\dot {X}$
below
 $p_{t}$
, then
$p_{t}$
, then  $$ \begin{align*} \hspace{-2pc} Y_{t}=\{\beta< \kappa:\exists r\in \text{split}(p)\text{ such that } t\unlhd r \text{ and }p_{r}\Vdash\check{\beta}\in\dot{X}\}.\end{align*} $$
$$ \begin{align*} \hspace{-2pc} Y_{t}=\{\beta< \kappa:\exists r\in \text{split}(p)\text{ such that } t\unlhd r \text{ and }p_{r}\Vdash\check{\beta}\in\dot{X}\}.\end{align*} $$
-
(2) Let
 $\dot {X}$
be an
$\dot {X}$
be an
 $\mathbb {S}_{\kappa }^{\lambda }$
-name for an infinite subset of
$\mathbb {S}_{\kappa }^{\lambda }$
-name for an infinite subset of
 $\kappa $
. If
$\kappa $
. If
 $p\in \mathbb {S}_{\kappa }^{\lambda }$
is preprocessed for
$p\in \mathbb {S}_{\kappa }^{\lambda }$
is preprocessed for
 $(\dot {X}, F\in [\text {supp}(p)]^{<\kappa })$
and
$(\dot {X}, F\in [\text {supp}(p)]^{<\kappa })$
and
 $\bar {\sigma }\in \Lambda (F)$
, then
$\bar {\sigma }\in \Lambda (F)$
, then  $$ \begin{align*}\hspace{-2.6pc}Y_{\bar{\sigma}}=\{\beta\in\kappa:\exists \bar{\tau}\in \Lambda(F^{\prime}) \text{ for } F^{\prime} \supseteq F, \lvert F^{\prime}\lvert <\kappa \text{ such that } \bar{\sigma}\sqsubseteq \bar{\tau} \text{ and }p_{\bar{\tau}}\Vdash\check{\beta}\in\dot{X}\}.\end{align*} $$
$$ \begin{align*}\hspace{-2.6pc}Y_{\bar{\sigma}}=\{\beta\in\kappa:\exists \bar{\tau}\in \Lambda(F^{\prime}) \text{ for } F^{\prime} \supseteq F, \lvert F^{\prime}\lvert <\kappa \text{ such that } \bar{\sigma}\sqsubseteq \bar{\tau} \text{ and }p_{\bar{\tau}}\Vdash\check{\beta}\in\dot{X}\}.\end{align*} $$
8
 $\kappa $
-Sacks indestructibility
$\kappa $
-Sacks indestructibility
In this section we set out to obtain our main result, namely the relative consistency of
![]() $\mathfrak {i}(\kappa )<2^{\kappa }$
. For this we start with a measurable cardinal
$\mathfrak {i}(\kappa )<2^{\kappa }$
. For this we start with a measurable cardinal
![]() $\kappa $
and a normal measure
$\kappa $
and a normal measure
![]() $\mathcal {U}$
on
$\mathcal {U}$
on
![]() $\kappa $
. Using the forcing notion
$\kappa $
. Using the forcing notion
![]() $\mathbb {P}_{\mathcal {U}}$
we adjoin a
$\mathbb {P}_{\mathcal {U}}$
we adjoin a
![]() $\mathcal {U}$
-supported
$\mathcal {U}$
-supported
![]() $\kappa $
-maximal independent family, which by Lemma 6.3 is densely maximal. A key feature of our proof is Lemma 6.2 which gives an equivalent characterisation of dense maximality via the property
$\kappa $
-maximal independent family, which by Lemma 6.3 is densely maximal. A key feature of our proof is Lemma 6.2 which gives an equivalent characterisation of dense maximality via the property
![]() $(\ast )$
of the same lemma. In fact, to show that
$(\ast )$
of the same lemma. In fact, to show that
![]() $\mathcal {A}=\mathcal {A}_{G}$
for a
$\mathcal {A}=\mathcal {A}_{G}$
for a
![]() $\mathbb {P}_{\mathcal {U}}$
-generic filter G remains maximal after forcing with a large product of
$\mathbb {P}_{\mathcal {U}}$
-generic filter G remains maximal after forcing with a large product of
![]() $\kappa $
-Sacks forcing, we show that the property
$\kappa $
-Sacks forcing, we show that the property
![]() $(\ast )$
is preserved. With other words, we show that in the final generic extension a
$(\ast )$
is preserved. With other words, we show that in the final generic extension a
![]() $\kappa $
-independent family which we adjoin via forcing at an initial step of the construction satisfies property
$\kappa $
-independent family which we adjoin via forcing at an initial step of the construction satisfies property
![]() $(\ast )$
. Note that in difference with the original work of Shelah [Reference Shelah22], we are only interested in products of
$(\ast )$
. Note that in difference with the original work of Shelah [Reference Shelah22], we are only interested in products of
![]() $\kappa $
-Sacks forcing and not iterations.
$\kappa $
-Sacks forcing and not iterations.
Theorem 8.1 (GCH).
Let
![]() $\kappa $
be a measurable cardinal, let
$\kappa $
be a measurable cardinal, let
![]() $\mathcal {U}$
be a normal measure on
$\mathcal {U}$
be a normal measure on
![]() $\kappa $
, and let G be
$\kappa $
, and let G be
![]() $\mathbb {P}_{\mathcal {U}}$
-generic filter over the ground model
$\mathbb {P}_{\mathcal {U}}$
-generic filter over the ground model
![]() $V_{0}$
. Let
$V_{0}$
. Let
![]() $\mathcal {A}=\mathcal {A}_{G}$
and
$\mathcal {A}=\mathcal {A}_{G}$
and
![]() $V=V_{0}[G]$
. Then
$V=V_{0}[G]$
. Then
Proof Note that GCH holds in V and
![]() $\kappa $
is inaccessible in V. By Lemma 6.3 the family
$\kappa $
is inaccessible in V. By Lemma 6.3 the family
![]() $\mathcal {A}$
is densely maximal in V. To prove that
$\mathcal {A}$
is densely maximal in V. To prove that
![]() $(\mathcal {A}\text { is densely maximal})^{V^{\mathbb {S}_{\kappa }}}$
we will show that in
$(\mathcal {A}\text { is densely maximal})^{V^{\mathbb {S}_{\kappa }}}$
we will show that in
![]() $V^{\mathbb {S}_{\kappa }}$
, property
$V^{\mathbb {S}_{\kappa }}$
, property
![]() $(*)$
of
$(*)$
of
![]() $\mathcal {A}$
from Lemma 6.2 holds. More precisely, we will show that in
$\mathcal {A}$
from Lemma 6.2 holds. More precisely, we will show that in
![]() $V^{\mathbb {S}_{\kappa }}$
for each
$V^{\mathbb {S}_{\kappa }}$
for each
![]() $X\subseteq \kappa $
and each
$X\subseteq \kappa $
and each
![]() $h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
such that
$h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
such that
![]() $X\subseteq \mathcal {A}^{h}$
property
$X\subseteq \mathcal {A}^{h}$
property
![]() $(*)_{X,h}$
holds, where
$(*)_{X,h}$
holds, where
![]() $(*)_{X,h}$
either
$(*)_{X,h}$
either
![]() $\exists B\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
such that
$\exists B\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
such that
![]() $\mathcal {A}^{h}\backslash X\subseteq B$
or there is
$\mathcal {A}^{h}\backslash X\subseteq B$
or there is
![]() $h^{\prime }\supseteq h$
such that
$h^{\prime }\supseteq h$
such that
![]() $\mathcal {A}^{h^{\prime }}\subseteq \mathcal {A}^{h}\backslash X$
.
$\mathcal {A}^{h^{\prime }}\subseteq \mathcal {A}^{h}\backslash X$
.
Suppose not. Thus, there are
![]() $X\subseteq \kappa $
,
$X\subseteq \kappa $
,
![]() $h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
such that
$h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
such that
![]() $X\subseteq \mathcal {A}^{h}$
and
$X\subseteq \mathcal {A}^{h}$
and
![]() $\lnot (*)_{X,h}$
. That is,
$\lnot (*)_{X,h}$
. That is,
Let
![]() $\dot {X}$
be an
$\dot {X}$
be an
![]() $\mathbb {S}_{\kappa }$
-name for X in V and let
$\mathbb {S}_{\kappa }$
-name for X in V and let
![]() $p\in \mathbb {S}_{\kappa }$
force the above. By Lemma 7.9 we can assume that p is preprocessed for
$p\in \mathbb {S}_{\kappa }$
force the above. By Lemma 7.9 we can assume that p is preprocessed for
![]() $\dot {X}$
and by Corollary 7.15 that for each
$\dot {X}$
and by Corollary 7.15 that for each
![]() $t\in \operatorname {\mathrm {split}}(p)$
for the outer hull
$t\in \operatorname {\mathrm {split}}(p)$
for the outer hull
![]() $Y_{t}$
of
$Y_{t}$
of
![]() $\dot {X}$
below
$\dot {X}$
below
![]() $p_{t}$
is of the form
$p_{t}$
is of the form
![]() $Y_{t}=\{\beta < \kappa :\exists r\in \text {split}(p)\text { such that }t\unlhd r\text { or }r\unlhd t\text { and }p_{r}\Vdash \check {\beta }\in \dot {X}\}$
.
$Y_{t}=\{\beta < \kappa :\exists r\in \text {split}(p)\text { such that }t\unlhd r\text { or }r\unlhd t\text { and }p_{r}\Vdash \check {\beta }\in \dot {X}\}$
.
Claim 8.2. Let
![]() $t\in \operatorname {\mathrm {split}}(p)$
. Then
$t\in \operatorname {\mathrm {split}}(p)$
. Then
![]() $Y_{t}\subseteq \mathcal {A}^{h}$
.
$Y_{t}\subseteq \mathcal {A}^{h}$
.
Proof Let
![]() $m\in Y_{t}$
. Thus there is
$m\in Y_{t}$
. Thus there is
![]() $q_{t,m}\leq p_{t}$
such that
$q_{t,m}\leq p_{t}$
such that
![]() $q_{t,m}\Vdash \check {m}\in \dot {X}$
. But
$q_{t,m}\Vdash \check {m}\in \dot {X}$
. But
![]() $p_{t}\Vdash \dot {X}\subseteq \mathcal {A}^{h}$
and so m must be an element of
$p_{t}\Vdash \dot {X}\subseteq \mathcal {A}^{h}$
and so m must be an element of
![]() $\mathcal {A}^{h}$
.
$\mathcal {A}^{h}$
.
We will make use of the following function
![]() $H\in {^{\kappa }\kappa }\cap V$
. Given
$H\in {^{\kappa }\kappa }\cap V$
. Given
![]() $t\in \operatorname {\mathrm {split}}(p)$
and
$t\in \operatorname {\mathrm {split}}(p)$
and
![]() $\beta \in Y_{t}$
, let
$\beta \in Y_{t}$
, let
![]() $r(t,\beta )$
be a witness to
$r(t,\beta )$
be a witness to
![]() $\beta \in Y_{t}$
such that t is comparable with
$\beta \in Y_{t}$
such that t is comparable with
![]() $r(t,\beta )$
and
$r(t,\beta )$
and
![]() $r(t,\beta )$
is of least splitting level. Then define
$r(t,\beta )$
is of least splitting level. Then define
where if
![]() $r(t,\beta )$
is not defined, i.e.,
$r(t,\beta )$
is not defined, i.e.,
![]() $\beta \notin Y_{t}$
, then we take
$\beta \notin Y_{t}$
, then we take
![]() $\operatorname {\mathrm {sl}}(r(t,\beta ))=0$
.
$\operatorname {\mathrm {sl}}(r(t,\beta ))=0$
.
Fix
![]() $t\in \operatorname {\mathrm {split}}(p)$
. Since
$t\in \operatorname {\mathrm {split}}(p)$
. Since
![]() $Y_{t}\subseteq \mathcal {A}^{h}$
, by the dense maximality of
$Y_{t}\subseteq \mathcal {A}^{h}$
, by the dense maximality of
![]() $\mathcal {A}$
in V either there is
$\mathcal {A}$
in V either there is
![]() $B\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
such that
$B\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
such that
![]() $\mathcal {A}^{h}\backslash Y_{t}\subseteq B$
or there is
$\mathcal {A}^{h}\backslash Y_{t}\subseteq B$
or there is
![]() $h^{\prime }\supseteq h$
such that
$h^{\prime }\supseteq h$
such that
![]() $\mathcal {A}^{h^{\prime }}\subseteq \mathcal {A}^{h}\backslash Y_{t}$
. In the latter case,
$\mathcal {A}^{h^{\prime }}\subseteq \mathcal {A}^{h}\backslash Y_{t}$
. In the latter case,
![]() $\mathcal {A}^{h^{\prime }}\cap Y_{t}=\emptyset $
and since
$\mathcal {A}^{h^{\prime }}\cap Y_{t}=\emptyset $
and since
![]() $p\Vdash \dot {X}\subseteq \check {Y}_{t}$
, we obtain that
$p\Vdash \dot {X}\subseteq \check {Y}_{t}$
, we obtain that
![]() $p\Vdash \mathcal {A}^{h^{\prime }}\cap \dot {X}=\emptyset $
, contrary to the choice of p. Thus, we can assume that
$p\Vdash \mathcal {A}^{h^{\prime }}\cap \dot {X}=\emptyset $
, contrary to the choice of p. Thus, we can assume that
![]() $\forall t\in \operatorname {\mathrm {split}}(p)\exists B_{t}\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
such that
$\forall t\in \operatorname {\mathrm {split}}(p)\exists B_{t}\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
such that
![]() $\mathcal {A}^{h}\backslash Y_{t}\subseteq B_{t}$
,
$\mathcal {A}^{h}\backslash Y_{t}\subseteq B_{t}$
,
![]() $\mathcal {A}^{h}\backslash Y_{t}\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
. But then
$\mathcal {A}^{h}\backslash Y_{t}\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
. But then
![]() $Y_{t}\cup \kappa \backslash \mathcal {A}^{h}\in \operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
. Now, since
$Y_{t}\cup \kappa \backslash \mathcal {A}^{h}\in \operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
. Now, since
![]() $\operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
is a
$\operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
is a
![]() $\kappa $
-p-set, there is
$\kappa $
-p-set, there is
![]() $C\in \operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
such that
$C\in \operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
such that
![]() $C\subseteq ^{*} Y_{t}\cup \kappa \backslash \mathcal {A}^{h}$
for each
$C\subseteq ^{*} Y_{t}\cup \kappa \backslash \mathcal {A}^{h}$
for each
![]() $t\in \operatorname {\mathrm {split}}(p)$
. Thus in particular,
$t\in \operatorname {\mathrm {split}}(p)$
. Thus in particular,
![]() $C\cap \mathcal {A}^{h}\subseteq ^{*} Y_{t}$
for all
$C\cap \mathcal {A}^{h}\subseteq ^{*} Y_{t}$
for all
![]() $t\in \operatorname {\mathrm {split}}(p)$
and so we can find a function
$t\in \operatorname {\mathrm {split}}(p)$
and so we can find a function
![]() $f\in V\cap {^{\kappa }\kappa }$
such that
$f\in V\cap {^{\kappa }\kappa }$
such that
Equivalently, for each
![]() $\alpha \in \kappa $
,
$\alpha \in \kappa $
,
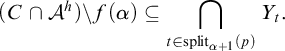 $$ \begin{align*}(C\cap\mathcal{A}^{h})\backslash f(\alpha)\subseteq \bigcap_{t\in\operatorname{\mathrm{split}}_{\alpha+1}(p)}Y_{t}.\end{align*} $$
$$ \begin{align*}(C\cap\mathcal{A}^{h})\backslash f(\alpha)\subseteq \bigcap_{t\in\operatorname{\mathrm{split}}_{\alpha+1}(p)}Y_{t}.\end{align*} $$
Moreover, we can assume that
![]() $H(\alpha )+1 < f(\alpha )$
and that f is strictly increasing.
$H(\alpha )+1 < f(\alpha )$
and that f is strictly increasing.
Now, we use Corollary 5.7 for the strictly increasing function
![]() $f^{2}=f\circ f$
, i.e., the composition of f with itself. Then there is a set
$f^{2}=f\circ f$
, i.e., the composition of f with itself. Then there is a set
![]() $C^{*}\in \operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
such that
$C^{*}\in \operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
such that
![]() $\forall \alpha \in C^{*}\forall \gamma \in \alpha \cap C^{*} (f^{2}(\gamma )<\alpha )$
. Now, let
$\forall \alpha \in C^{*}\forall \gamma \in \alpha \cap C^{*} (f^{2}(\gamma )<\alpha )$
. Now, let
![]() $C^{\prime }=C \cap C^{*} \cap (f(1),\kappa )$
. Thus
$C^{\prime }=C \cap C^{*} \cap (f(1),\kappa )$
. Thus
![]() $C^{\prime }\in \operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
. Let
$C^{\prime }\in \operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
. Let
![]() $\{k(\alpha ): \alpha <\kappa \}$
be an increasing enumeration of
$\{k(\alpha ): \alpha <\kappa \}$
be an increasing enumeration of
![]() $C^{\prime } \cap \mathcal {A}^{h}$
. Since
$C^{\prime } \cap \mathcal {A}^{h}$
. Since
![]() $C^{\prime }\in \operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
the latter set is indeed unbounded in
$C^{\prime }\in \operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
the latter set is indeed unbounded in
![]() $\kappa $
. Recursively, we will define a fusion sequence
$\kappa $
. Recursively, we will define a fusion sequence
![]() $\tau =\langle q_{\alpha }:\alpha \in \kappa \rangle $
below p such that:
$\tau =\langle q_{\alpha }:\alpha \in \kappa \rangle $
below p such that:
-
(1)
 $q_{\alpha +1} \leq _{\alpha } q_{\alpha }$
.
$q_{\alpha +1} \leq _{\alpha } q_{\alpha }$
. -
(2)
 $q_{\alpha +1} \Vdash k(\alpha ) \in \dot {X}$
.
$q_{\alpha +1} \Vdash k(\alpha ) \in \dot {X}$
. -
(3) If q is the fusion of
 $\tau $
then
$\tau $
then
 $q\Vdash C^{\prime }\cap \mathcal {A}^{h}\subseteq \dot {X}$
.
$q\Vdash C^{\prime }\cap \mathcal {A}^{h}\subseteq \dot {X}$
.
But then, since
![]() $q\Vdash \mathcal {A}^{h}\backslash \dot {X}\subseteq \mathcal {A}^{h}\backslash C^{\prime }$
and
$q\Vdash \mathcal {A}^{h}\backslash \dot {X}\subseteq \mathcal {A}^{h}\backslash C^{\prime }$
and
![]() $\mathcal {A}^{h}\backslash C^{\prime }\subseteq \kappa \backslash C^{\prime }\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
, we obtain that
$\mathcal {A}^{h}\backslash C^{\prime }\subseteq \kappa \backslash C^{\prime }\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
, we obtain that
![]() $q\Vdash \mathcal {A}^{h}\backslash \dot {X}\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
, which is again a contradiction to the choice of p.
$q\Vdash \mathcal {A}^{h}\backslash \dot {X}\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
, which is again a contradiction to the choice of p.
Here is the construction of
![]() $\tau $
. Start with
$\tau $
. Start with
![]() $q_{0} =p$
and at limits take intersections. Consider
$q_{0} =p$
and at limits take intersections. Consider
![]() $k(0)$
and put
$k(0)$
and put
![]() $r = \operatorname {\mathrm {stem}}(p)$
. Since
$r = \operatorname {\mathrm {stem}}(p)$
. Since
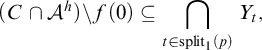 $$ \begin{align*}(C\cap\mathcal{A}^{h})\backslash f(0)\subseteq \bigcap_{t\in\text{split}_{1}(p)} Y_{t},\end{align*} $$
$$ \begin{align*}(C\cap\mathcal{A}^{h})\backslash f(0)\subseteq \bigcap_{t\in\text{split}_{1}(p)} Y_{t},\end{align*} $$
for each
![]() $j \in \{0,1\}$
and p is preprocessed for
$j \in \{0,1\}$
and p is preprocessed for
![]() $\dot {X}$
there is
$\dot {X}$
there is
![]() $r_{j}(t,k(0))\in \operatorname {\mathrm {split}}_{H(k(0))}(p)$
such that
$r_{j}(t,k(0))\in \operatorname {\mathrm {split}}_{H(k(0))}(p)$
such that
![]() $p_{r_{j}(t,k(0))}\Vdash \check {k}(0)\in \dot {X}$
. Let
$p_{r_{j}(t,k(0))}\Vdash \check {k}(0)\in \dot {X}$
. Let
![]() $q_{1}=\bigcup \{p_{r_{j}(t,k(0))}: t\in \operatorname {\mathrm {split}}_{1}(p) , j \in \{0,1\}\}$
. Thus
$q_{1}=\bigcup \{p_{r_{j}(t,k(0))}: t\in \operatorname {\mathrm {split}}_{1}(p) , j \in \{0,1\}\}$
. Thus
![]() $q_{1}\leq _{0} q_{0}$
as we wanted.
$q_{1}\leq _{0} q_{0}$
as we wanted.
For completeness we present the construction of the next step: take
![]() $k(1)$
and
$k(1)$
and
![]() $t \in \operatorname {\mathrm {split}}_{1}(q_{1})$
. Note that
$t \in \operatorname {\mathrm {split}}_{1}(q_{1})$
. Note that
![]() $\operatorname {\mathrm {split}}_{1}(q_{1})= \operatorname {\mathrm {split}}_{\delta }(p)$
for some
$\operatorname {\mathrm {split}}_{1}(q_{1})= \operatorname {\mathrm {split}}_{\delta }(p)$
for some
![]() $1 \leq \delta \leq H(k(0))\leq f(k(0))$
and since
$1 \leq \delta \leq H(k(0))\leq f(k(0))$
and since
![]() $f^{2}(k(0)) < k(1)$
and
$f^{2}(k(0)) < k(1)$
and
![]() $C \backslash Y_{r} \subseteq f(f(k(0)))$
for all
$C \backslash Y_{r} \subseteq f(f(k(0)))$
for all
![]() $r \in \operatorname {\mathrm {split}}_{f(k(0))+1}(p)$
, we obtain
$r \in \operatorname {\mathrm {split}}_{f(k(0))+1}(p)$
, we obtain
![]() $k(1) \in Y_{r}$
for all
$k(1) \in Y_{r}$
for all
![]() $r \in \operatorname {\mathrm {split}}_{f(k(0))+1}(p)$
. Using the fact that p is preprocessed and repeating the argument above, find for each
$r \in \operatorname {\mathrm {split}}_{f(k(0))+1}(p)$
. Using the fact that p is preprocessed and repeating the argument above, find for each
![]() $j \in \{0,1\}$
an extension
$j \in \{0,1\}$
an extension
![]() $r_{j}(t,k(1))\leq p_{t^{\frown } j}$
such that
$r_{j}(t,k(1))\leq p_{t^{\frown } j}$
such that
![]() $r_{j}(t,k(1)) \Vdash k(1) \in \dot {X}$
. Let
$r_{j}(t,k(1)) \Vdash k(1) \in \dot {X}$
. Let
![]() $q_{2} = \bigcup \{r_{j}(t,k(1)): t \in \operatorname {\mathrm {split}}_{1}(q_{1}) \wedge j \in \{0,1\} \}$
. Then
$q_{2} = \bigcup \{r_{j}(t,k(1)): t \in \operatorname {\mathrm {split}}_{1}(q_{1}) \wedge j \in \{0,1\} \}$
. Then
![]() $q_{2}$
is a condition,
$q_{2}$
is a condition,
![]() $q_{2} \leq _{1} q_{1}$
, and
$q_{2} \leq _{1} q_{1}$
, and
![]() $q_{2} \Vdash k(1) \in \dot {X}$
.
$q_{2} \Vdash k(1) \in \dot {X}$
.
In general, suppose we have constructed
![]() $q_{\alpha }$
and consider
$q_{\alpha }$
and consider
![]() $k(\alpha )$
, and
$k(\alpha )$
, and
![]() $t \in \operatorname {\mathrm {split}}_{\alpha }(q_{\alpha })$
, then there is
$t \in \operatorname {\mathrm {split}}_{\alpha }(q_{\alpha })$
, then there is
![]() $\delta \geq \alpha $
so that
$\delta \geq \alpha $
so that
![]() $t \in \operatorname {\mathrm {split}}_{\delta } (p)$
and
$t \in \operatorname {\mathrm {split}}_{\delta } (p)$
and
![]() $\delta \leq H(k(\alpha ))$
. Again, since
$\delta \leq H(k(\alpha ))$
. Again, since
![]() $f^{2}(k(\alpha )) < k(\alpha +1)$
and
$f^{2}(k(\alpha )) < k(\alpha +1)$
and
![]() $C \backslash Y_{r} \subseteq f(f(k(\alpha )))$
for all
$C \backslash Y_{r} \subseteq f(f(k(\alpha )))$
for all
![]() $r \in \operatorname {\mathrm {split}}_{f(k(\alpha ))+1}(p)$
we get that
$r \in \operatorname {\mathrm {split}}_{f(k(\alpha ))+1}(p)$
we get that
![]() $k(\alpha ) \in Y_{t}$
, so again use that p is preprocessed and repeat the argument above to find conditions
$k(\alpha ) \in Y_{t}$
, so again use that p is preprocessed and repeat the argument above to find conditions
![]() $r_{j}(t,k(\alpha )) \leq p_{t^{\smallfrown } j}$
forcing
$r_{j}(t,k(\alpha )) \leq p_{t^{\smallfrown } j}$
forcing
![]() $r_{j}(t,k(\alpha )) \Vdash k(\alpha ) \in \dot {X} j \in \{0,1\}$
. Put
$r_{j}(t,k(\alpha )) \Vdash k(\alpha ) \in \dot {X} j \in \{0,1\}$
. Put
![]() $q_{\alpha +1} = \bigcup \{r_{j}(t,k(\alpha )): t \in \operatorname {\mathrm {split}}_{\alpha }(q_{\alpha }) \wedge j \in \{0,1\} \}$
. Then
$q_{\alpha +1} = \bigcup \{r_{j}(t,k(\alpha )): t \in \operatorname {\mathrm {split}}_{\alpha }(q_{\alpha }) \wedge j \in \{0,1\} \}$
. Then
![]() $q_{\alpha +1}$
is a condition,
$q_{\alpha +1}$
is a condition,
![]() $q_{\alpha +1} \leq _{\alpha } q_{\alpha }$
, and
$q_{\alpha +1} \leq _{\alpha } q_{\alpha }$
, and
![]() $q_{\alpha +1} \Vdash k(\alpha ) \in \dot {X}$
.
$q_{\alpha +1} \Vdash k(\alpha ) \in \dot {X}$
.
Theorem 8.3. The generic maximal independent family adjoined by
![]() $\mathbb {P}_{\mathcal {U}}$
over a model
$\mathbb {P}_{\mathcal {U}}$
over a model
![]() $V_{0}$
of GCH remains maximal after the
$V_{0}$
of GCH remains maximal after the
![]() $\kappa $
-support product
$\kappa $
-support product
![]() $\mathbb {S}_{\kappa }^{\lambda }$
.
$\mathbb {S}_{\kappa }^{\lambda }$
.
Proof The idea for this proof is not much different than the one for the successor step; however, the fusion argument has to be handled more carefully. We give now an outline with the most important details. As in the case above start with a densely maximal independent family
![]() $\mathcal {A}$
in
$\mathcal {A}$
in
![]() $V=V^{\mathbb {P}_{\mathcal {U}}}$
. To prove that
$V=V^{\mathbb {P}_{\mathcal {U}}}$
. To prove that
we will show that in
![]() $V^{\mathbb {S}_{\kappa }^{\lambda }}$
, property
$V^{\mathbb {S}_{\kappa }^{\lambda }}$
, property
![]() $(*)$
from Lemma 6.2 holds for the family
$(*)$
from Lemma 6.2 holds for the family
![]() $\mathcal {A}$
. Specifically, we show that in
$\mathcal {A}$
. Specifically, we show that in
![]() $V^{\mathbb {S}_{\kappa }^{\lambda }}$
for each
$V^{\mathbb {S}_{\kappa }^{\lambda }}$
for each
![]() $X\subseteq \kappa $
and each
$X\subseteq \kappa $
and each
![]() $h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
such that
$h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
such that
![]() $X\subseteq \mathcal {A}^{h}$
property
$X\subseteq \mathcal {A}^{h}$
property
![]() $(*)_{X,h}$
holds, where
$(*)_{X,h}$
holds, where
![]() $(*)_{X,h}$
states:
$(*)_{X,h}$
states:
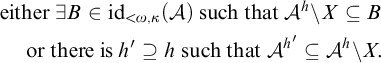 $$ \begin{align*}& \text{either }\exists B\in\operatorname{\mathrm{id}}_{<\omega,\kappa}(\mathcal{A})\text{ such that }\mathcal{A}^{h}\backslash X\subseteq B \\ & \quad\text{ or there is }h^{\prime}\supseteq h\text{ such that }\mathcal{A}^{h^{\prime}}\subseteq\mathcal{A}^{h}\backslash X.\end{align*} $$
$$ \begin{align*}& \text{either }\exists B\in\operatorname{\mathrm{id}}_{<\omega,\kappa}(\mathcal{A})\text{ such that }\mathcal{A}^{h}\backslash X\subseteq B \\ & \quad\text{ or there is }h^{\prime}\supseteq h\text{ such that }\mathcal{A}^{h^{\prime}}\subseteq\mathcal{A}^{h}\backslash X.\end{align*} $$
Suppose not. Thus, there are
![]() $X\subseteq \kappa $
,
$X\subseteq \kappa $
,
![]() $h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
such that
$h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})$
such that
![]() $X\subseteq \mathcal {A}^{h}$
and
$X\subseteq \mathcal {A}^{h}$
and
![]() $\lnot (*)_{X,h}$
. That is,
$\lnot (*)_{X,h}$
. That is,
Let
![]() $\dot {X}$
be an
$\dot {X}$
be an
![]() $\mathbb {S}_{\kappa }^{\lambda }$
-name for X in V and let
$\mathbb {S}_{\kappa }^{\lambda }$
-name for X in V and let
![]() $p\in \mathbb {S}_{\kappa }^{\lambda }$
force the above. Passing to a stronger condition if necessary we can assume that p is preprocessed for
$p\in \mathbb {S}_{\kappa }^{\lambda }$
force the above. Passing to a stronger condition if necessary we can assume that p is preprocessed for
![]() $\dot {X}$
. Now, for every
$\dot {X}$
. Now, for every
![]() $\alpha < \kappa $
and all
$\alpha < \kappa $
and all
![]() $F \subseteq \operatorname {\mathrm {supp}}(p)$
such that
$F \subseteq \operatorname {\mathrm {supp}}(p)$
such that
![]() $\lvert F \lvert < \kappa $
consider the set
$\lvert F \lvert < \kappa $
consider the set
![]() $\Lambda ^{F}_{\alpha }(p)$
. This is a set of size
$\Lambda ^{F}_{\alpha }(p)$
. This is a set of size
![]() $<\!\kappa $
because
$<\!\kappa $
because
![]() $\lvert \operatorname {\mathrm {split}}_{\alpha }(p(i)) \lvert \leq 2^{\lvert \alpha \lvert }$
and
$\lvert \operatorname {\mathrm {split}}_{\alpha }(p(i)) \lvert \leq 2^{\lvert \alpha \lvert }$
and
![]() $\lvert F \lvert < \kappa $
. Also,
$\lvert F \lvert < \kappa $
. Also,
![]() $\{\Lambda ^{F}_{\alpha }(p): \alpha <\kappa \wedge F \subseteq \operatorname {\mathrm {supp}}(p) \wedge \lvert F \lvert < \kappa \}$
has size
$\{\Lambda ^{F}_{\alpha }(p): \alpha <\kappa \wedge F \subseteq \operatorname {\mathrm {supp}}(p) \wedge \lvert F \lvert < \kappa \}$
has size
![]() $\kappa $
and so does its union.
$\kappa $
and so does its union.
Similarly to Claim 8.2 we obtain:
Claim 8.4. For all
![]() $\alpha < \kappa $
and
$\alpha < \kappa $
and
![]() $F \subseteq \operatorname {\mathrm {supp}}(p)$
such that
$F \subseteq \operatorname {\mathrm {supp}}(p)$
such that
![]() $\lvert F \lvert <\kappa $
, if
$\lvert F \lvert <\kappa $
, if
![]() $\bar {\sigma } \in \Lambda ^{F}_{\alpha }(p)$
then
$\bar {\sigma } \in \Lambda ^{F}_{\alpha }(p)$
then
![]() $Y_{\bar {\sigma }}\subseteq \mathcal {A}^{h}$
.
$Y_{\bar {\sigma }}\subseteq \mathcal {A}^{h}$
.
Before proceeding with construction of a fusion sequence, which will lead to the desired contradiction, we need to define one more auxiliary object, namely the function H defined below. Whenever
![]() $\bar {\sigma } \in \Lambda ^{F}_{\alpha }(p)$
and
$\bar {\sigma } \in \Lambda ^{F}_{\alpha }(p)$
and
![]() $\beta \in Y_{\bar {\sigma }}$
, let
$\beta \in Y_{\bar {\sigma }}$
, let
![]() $r(\bar {\sigma },\beta )$
be a witness to
$r(\bar {\sigma },\beta )$
be a witness to
![]() $\beta \in Y_{\bar {\sigma }}$
such that for each
$\beta \in Y_{\bar {\sigma }}$
such that for each
![]() $i \in F $
the stem of the condition
$i \in F $
the stem of the condition
![]() $r(\bar {\sigma },\beta )(i)$
is of minimal height. Define
$r(\bar {\sigma },\beta )(i)$
is of minimal height. Define
![]() $H\in {^{\kappa }\kappa }\cap V$
as follows:
$H\in {^{\kappa }\kappa }\cap V$
as follows:
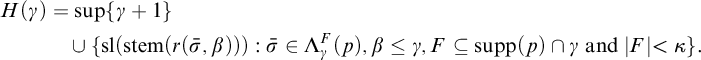 $$ \begin{align*}H(\gamma) & =\sup\{\gamma+1\} \\& \quad\cup\{\operatorname{\mathrm{sl}}(\operatorname{\mathrm{stem}}(r(\bar{\sigma},\beta))): \bar{\sigma} \in \Lambda_{\gamma}^{F}(p), \beta\leq \gamma, F\subseteq \operatorname{\mathrm{supp}}(p)\cap \gamma \text{ and } \lvert F \lvert <\kappa \}.\end{align*} $$
$$ \begin{align*}H(\gamma) & =\sup\{\gamma+1\} \\& \quad\cup\{\operatorname{\mathrm{sl}}(\operatorname{\mathrm{stem}}(r(\bar{\sigma},\beta))): \bar{\sigma} \in \Lambda_{\gamma}^{F}(p), \beta\leq \gamma, F\subseteq \operatorname{\mathrm{supp}}(p)\cap \gamma \text{ and } \lvert F \lvert <\kappa \}.\end{align*} $$
Again, following the argument for the single step, we can assume that for all
![]() $\alpha <\kappa $
and all
$\alpha <\kappa $
and all
![]() $\bar {\sigma } \in \Lambda _{\alpha }^{F}(p)$
there exists
$\bar {\sigma } \in \Lambda _{\alpha }^{F}(p)$
there exists
![]() $B_{\bar {\sigma }}\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
such that
$B_{\bar {\sigma }}\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
such that
![]() $\mathcal {A}^{h}\backslash Y_{\bar {\sigma }} \subseteq B_{\bar {\sigma }}$
,
$\mathcal {A}^{h}\backslash Y_{\bar {\sigma }} \subseteq B_{\bar {\sigma }}$
,
![]() $\mathcal {A}^{h}\backslash Y_{\bar {\sigma }}\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
. But then
$\mathcal {A}^{h}\backslash Y_{\bar {\sigma }}\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
. But then
![]() $Y_{\bar {\sigma }}\cup \kappa \backslash \mathcal {A}^{h}\in \operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
. Now, since
$Y_{\bar {\sigma }}\cup \kappa \backslash \mathcal {A}^{h}\in \operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
. Now, since
![]() $\operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
is a
$\operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
is a
![]() $\kappa $
-p-set, there is
$\kappa $
-p-set, there is
![]() $C\in \operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
such that
$C\in \operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
such that
![]() $C\subseteq ^{*} Y_{\bar {\sigma }}\cup \kappa \backslash \mathcal {A}^{h}$
for each
$C\subseteq ^{*} Y_{\bar {\sigma }}\cup \kappa \backslash \mathcal {A}^{h}$
for each
![]() $\bar {\sigma } \in \Lambda _{\alpha }^{F}$
. Thus in particular,
$\bar {\sigma } \in \Lambda _{\alpha }^{F}$
. Thus in particular,
![]() $C\cap \mathcal {A}^{h}\subseteq Y_{\bar {\sigma }}$
for each
$C\cap \mathcal {A}^{h}\subseteq Y_{\bar {\sigma }}$
for each
![]() $\bar {\sigma } \in \Lambda _{\alpha }^{F}(p)$
and so we can find a function
$\bar {\sigma } \in \Lambda _{\alpha }^{F}(p)$
and so we can find a function
![]() $f\in V\cap {^{\kappa }\kappa }$
such that,
$f\in V\cap {^{\kappa }\kappa }$
such that,
Thus, for each
![]() $\alpha \in \kappa $
,
$\alpha \in \kappa $
,
![]() $\bar {\sigma } \in \Lambda ^{F}_{\alpha +1}(p)$
, and
$\bar {\sigma } \in \Lambda ^{F}_{\alpha +1}(p)$
, and
![]() $\beta \in C\cap \mathcal {A}^{h}$
, if
$\beta \in C\cap \mathcal {A}^{h}$
, if
![]() $\beta>f(\alpha )$
then
$\beta>f(\alpha )$
then
![]() $\beta \in Y_{\bar {\sigma }}$
. Moreover, we can assume that f is strictly increasing, that
$\beta \in Y_{\bar {\sigma }}$
. Moreover, we can assume that f is strictly increasing, that
![]() $H(\alpha )\leq f(\alpha )$
and
$H(\alpha )\leq f(\alpha )$
and
![]() $\alpha +2<f(\alpha )$
for all
$\alpha +2<f(\alpha )$
for all
![]() $\alpha \in \kappa $
.
$\alpha \in \kappa $
.
By Corollary 5.7, there is
![]() $C^{*}\in \operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
such that
$C^{*}\in \operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
such that
![]() $\forall \alpha \in C^{*}\forall \gamma \in \alpha \cap C^{*} (f^{2}(\gamma )<\alpha )$
. Now, let
$\forall \alpha \in C^{*}\forall \gamma \in \alpha \cap C^{*} (f^{2}(\gamma )<\alpha )$
. Now, let
![]() $C^{\prime }=C \cap C^{*} \cap (f(0),\kappa )$
. Thus
$C^{\prime }=C \cap C^{*} \cap (f(0),\kappa )$
. Thus
![]() $C^{\prime }\in \operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
. Let
$C^{\prime }\in \operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
. Let
![]() $\{k(\alpha ): \alpha \in \kappa \}$
be an increasing enumeration of
$\{k(\alpha ): \alpha \in \kappa \}$
be an increasing enumeration of
![]() $C^{\prime } \cap \mathcal {A}^{h}$
. Since
$C^{\prime } \cap \mathcal {A}^{h}$
. Since
![]() $C^{\prime }\in \operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
the latter set is indeed unbounded in
$C^{\prime }\in \operatorname {\mathrm {fil}}_{<\omega ,\kappa }(\mathcal {A})$
the latter set is indeed unbounded in
![]() $\kappa $
. Recursively, we will define a fusion sequence
$\kappa $
. Recursively, we will define a fusion sequence
![]() $\tau =\langle q_{\alpha }, F_{\alpha }:\alpha \in \kappa \rangle \subseteq \mathbb {S}_{\kappa }^{\lambda }$
below p, ordinals
$\tau =\langle q_{\alpha }, F_{\alpha }:\alpha \in \kappa \rangle \subseteq \mathbb {S}_{\kappa }^{\lambda }$
below p, ordinals
![]() $(\eta _{\alpha }: \alpha < \kappa )$
, and bijections
$(\eta _{\alpha }: \alpha < \kappa )$
, and bijections
![]() $g_{\alpha }: F_{\alpha } \to \eta _{\alpha }$
such that for all
$g_{\alpha }: F_{\alpha } \to \eta _{\alpha }$
such that for all
![]() $\alpha <\kappa $
:
$\alpha <\kappa $
:
-
(1)
 $q_{\alpha +1} \leq _{F_{\alpha },\alpha } q_{\alpha }.$
.
$q_{\alpha +1} \leq _{F_{\alpha },\alpha } q_{\alpha }.$
. -
(2)
 $\eta _{\alpha } \geq \alpha $
$\eta _{\alpha } \geq \alpha $
-
(3) For all
 $\alpha < \alpha ^{\prime }<\kappa $
,
$\alpha < \alpha ^{\prime }<\kappa $
,
 $g_{\alpha } \subseteq g_{\alpha ^{\prime }}$
, and for limit ordinals
$g_{\alpha } \subseteq g_{\alpha ^{\prime }}$
, and for limit ordinals
 $\delta < \kappa g_{\delta } = \bigcup _{\alpha < \delta } g_{\alpha }$
.
$\delta < \kappa g_{\delta } = \bigcup _{\alpha < \delta } g_{\alpha }$
. -
(4)
 $q_{\alpha +1} \Vdash k(\alpha ) \in \dot {X}$
.
$q_{\alpha +1} \Vdash k(\alpha ) \in \dot {X}$
.
Now, if q is the fusion of
![]() $\tau $
then
$\tau $
then
![]() $q\Vdash C^{\prime }\cap \mathcal {A}^{h}\subseteq \dot {X}$
. But then, since
$q\Vdash C^{\prime }\cap \mathcal {A}^{h}\subseteq \dot {X}$
. But then, since
![]() $q\Vdash \mathcal {A}^{h}\backslash \dot {X}\subseteq \mathcal {A}^{h}\backslash C^{\prime }$
and
$q\Vdash \mathcal {A}^{h}\backslash \dot {X}\subseteq \mathcal {A}^{h}\backslash C^{\prime }$
and
![]() $\mathcal {A}^{h}\backslash C^{\prime }\subseteq \omega \backslash C^{\prime }\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
, we obtain that
$\mathcal {A}^{h}\backslash C^{\prime }\subseteq \omega \backslash C^{\prime }\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
, we obtain that
![]() $q\Vdash \mathcal {A}^{h}\backslash \dot {X}\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
, contradicting the choice of p.
$q\Vdash \mathcal {A}^{h}\backslash \dot {X}\in \operatorname {\mathrm {id}}_{<\omega ,\kappa }(\mathcal {A})$
, contradicting the choice of p.
We proceed with the recursive construction of
![]() $\tau $
. Start with
$\tau $
. Start with
![]() $q_{0} = p$
,
$q_{0} = p$
,
![]() $F_{0}= \min (\operatorname {\mathrm {supp}}(p))$
,
$F_{0}= \min (\operatorname {\mathrm {supp}}(p))$
,
![]() $\eta _{0} = 0$
, and
$\eta _{0} = 0$
, and
![]() $g_{0}= \emptyset $
. At limit stages
$g_{0}= \emptyset $
. At limit stages
![]() $\delta <\kappa $
the construction of
$\delta <\kappa $
the construction of
![]() $q_{\delta }$
and
$q_{\delta }$
and
![]() $F_{\delta }$
it is already been determined so that the conditions in Definition 7.4 are fulfilled. Finally, let
$F_{\delta }$
it is already been determined so that the conditions in Definition 7.4 are fulfilled. Finally, let
![]() $\eta _{\delta } = \sup _{\alpha <\delta } \eta _{\alpha }$
and
$\eta _{\delta } = \sup _{\alpha <\delta } \eta _{\alpha }$
and
![]() $g_{\delta }$
as above. Consider
$g_{\delta }$
as above. Consider
![]() $k(0)$
and put
$k(0)$
and put
![]() $\bar {\sigma } = \langle \operatorname {\mathrm {stem}}(p(\min (\operatorname {\mathrm {supp}}(p))))\rangle $
. Since for all
$\bar {\sigma } = \langle \operatorname {\mathrm {stem}}(p(\min (\operatorname {\mathrm {supp}}(p))))\rangle $
. Since for all
![]() $\bar {\tau } \in \Lambda ^{F_{0}}_{1}(p)$
,
$\bar {\tau } \in \Lambda ^{F_{0}}_{1}(p)$
,
![]() $C \setminus Y_{\bar {\tau }} \subseteq f(0)$
,
$C \setminus Y_{\bar {\tau }} \subseteq f(0)$
,
![]() $k(0) \geq f(0)$
, and p is preprocessed for
$k(0) \geq f(0)$
, and p is preprocessed for
![]() $(\dot {X}, F_{0})$
we have that
$(\dot {X}, F_{0})$
we have that
![]() $k(0) \in Y_{\bar {\tau }}$
for all
$k(0) \in Y_{\bar {\tau }}$
for all
![]() $\bar {\tau } \in \Lambda ^{F_{0}}_{1}(p)$
and so, by Corollary 7.15 for each
$\bar {\tau } \in \Lambda ^{F_{0}}_{1}(p)$
and so, by Corollary 7.15 for each
![]() $h \in ^{F_{0}} 2$
there exists a set
$h \in ^{F_{0}} 2$
there exists a set
![]() $F_{0}^{\prime } \supseteq F_{0}$
, a
$F_{0}^{\prime } \supseteq F_{0}$
, a
![]() $\bar {\tau } \sqsupseteq \bar {\sigma }$
, and condition
$\bar {\tau } \sqsupseteq \bar {\sigma }$
, and condition
![]() $r_{h}(\bar {\tau }_{h},k(0)) \leq p^{h}_{\bar {\tau }_{h}}$
such that
$r_{h}(\bar {\tau }_{h},k(0)) \leq p^{h}_{\bar {\tau }_{h}}$
such that
![]() $r_{h}(\bar {\tau }_{h},k(0)) \Vdash k(0) \in \dot {X}$
.
$r_{h}(\bar {\tau }_{h},k(0)) \Vdash k(0) \in \dot {X}$
.
For completeness, we give a more detailed proof of the existence of the conditions
![]() $r_{h}(\bar {\tau }_{h},k(0))$
. Recall that
$r_{h}(\bar {\tau }_{h},k(0))$
. Recall that
![]() $p^{h}_{\bar {\sigma }}$
is defined as follows:
$p^{h}_{\bar {\sigma }}$
is defined as follows:
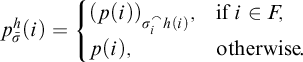 $$ \begin{align*}p^{h}_{\bar{\sigma}}(i) = \begin{cases} (p(i))_{ \sigma_{i}^{\smallfrown} h(i)}, & \text{if } i \in F, \\ p(i), & \text{otherwise. } \end{cases} \end{align*} $$
$$ \begin{align*}p^{h}_{\bar{\sigma}}(i) = \begin{cases} (p(i))_{ \sigma_{i}^{\smallfrown} h(i)}, & \text{if } i \in F, \\ p(i), & \text{otherwise. } \end{cases} \end{align*} $$
There are sequences
![]() $\bar {\sigma }^{\prime }_{h} \in \Lambda ^{F_{0}}_{1}(p)$
such that
$\bar {\sigma }^{\prime }_{h} \in \Lambda ^{F_{0}}_{1}(p)$
such that
![]() $\bar {\sigma }_{h} \unlhd \bar {\sigma }^{\prime }_{h}$
where
$\bar {\sigma }_{h} \unlhd \bar {\sigma }^{\prime }_{h}$
where
![]() $\bar {\sigma }_{h}$
is such that
$\bar {\sigma }_{h}$
is such that
![]() $\sigma _{h}(i)= \sigma (i)^{\frown } h(i)$
for all
$\sigma _{h}(i)= \sigma (i)^{\frown } h(i)$
for all
![]() $i \in F_{0}$
. Hence, using that p is preprocessed we can get a set
$i \in F_{0}$
. Hence, using that p is preprocessed we can get a set
![]() $F_{0}^{\prime } \supseteq F_{0}$
such that
$F_{0}^{\prime } \supseteq F_{0}$
such that
![]() $\lvert F_{0}^{\prime } \lvert < \kappa $
and sequences
$\lvert F_{0}^{\prime } \lvert < \kappa $
and sequences
![]() $\bar {\tau }_{h} \sqsupseteq \bar {\sigma }^{\prime }_{h}$
so that
$\bar {\tau }_{h} \sqsupseteq \bar {\sigma }^{\prime }_{h}$
so that
![]() $p_{\bar {\tau }_{h}} \Vdash k(0) \in \dot {X}$
. Thus, take
$p_{\bar {\tau }_{h}} \Vdash k(0) \in \dot {X}$
. Thus, take
![]() $r_{h}(\bar {\tau }_{h},k(0))=p_{\bar {\tau }_{h}}$
.
$r_{h}(\bar {\tau }_{h},k(0))=p_{\bar {\tau }_{h}}$
.
Then if
![]() $q_{1}= \bigcup \{ r_{h}(\bar {\sigma },k(0)) : h \in {^{F_{0}}} 2, \bar {\tau }_{h} \in \Lambda ^{F_{0}^{\prime }}_{0}(p) \}$
,
$q_{1}= \bigcup \{ r_{h}(\bar {\sigma },k(0)) : h \in {^{F_{0}}} 2, \bar {\tau }_{h} \in \Lambda ^{F_{0}^{\prime }}_{0}(p) \}$
,
![]() $F_{1}= F_{0}^{\prime } \cup \{\min \{\operatorname {\mathrm {supp}}(q_{1}) \backslash F_{0}^{\prime }\}\}$
,
$F_{1}= F_{0}^{\prime } \cup \{\min \{\operatorname {\mathrm {supp}}(q_{1}) \backslash F_{0}^{\prime }\}\}$
,
![]() $\eta _{1}= \eta _{0} +1$
, and
$\eta _{1}= \eta _{0} +1$
, and
![]() $g_{1} = g_{0} \cup \{ (\min \{\operatorname {\mathrm {supp}}(q_{1}) \backslash F_{0}^{\prime }, \eta _{1})\}$
we have that
$g_{1} = g_{0} \cup \{ (\min \{\operatorname {\mathrm {supp}}(q_{1}) \backslash F_{0}^{\prime }, \eta _{1})\}$
we have that
![]() $q_{1} \leq _{0,F_{0}^{\prime }} q_{0}\text { and }q_{1} \Vdash k(0) \in \dot {X}$
as we wanted.
$q_{1} \leq _{0,F_{0}^{\prime }} q_{0}\text { and }q_{1} \Vdash k(0) \in \dot {X}$
as we wanted.
In general, suppose we have constructed
![]() $q_{\alpha }$
,
$q_{\alpha }$
,
![]() $F_{\alpha }$
,
$F_{\alpha }$
,
![]() $\eta _{\alpha }$
, and
$\eta _{\alpha }$
, and
![]() $g_{\alpha }$
as desired. Consider
$g_{\alpha }$
as desired. Consider
![]() $k(\alpha )$
and the set
$k(\alpha )$
and the set
![]() $\Lambda ^{F_{\alpha }}_{\alpha +1}(p_{\alpha })$
. Fix an enumeration
$\Lambda ^{F_{\alpha }}_{\alpha +1}(p_{\alpha })$
. Fix an enumeration
![]() $\{\gamma _{l} =(\bar {\sigma }_{l}, h_{l}): l< \rho \}$
of all pairs of the form
$\{\gamma _{l} =(\bar {\sigma }_{l}, h_{l}): l< \rho \}$
of all pairs of the form
![]() $(\bar {\sigma }, h)$
such that
$(\bar {\sigma }, h)$
such that
![]() $\bar {\sigma } \in \Lambda _{\alpha +1}^{F_{\alpha }}(q_{\alpha })$
and
$\bar {\sigma } \in \Lambda _{\alpha +1}^{F_{\alpha }}(q_{\alpha })$
and
![]() $h \in {^{F_{\alpha }}2}$
. Note that the ordinal
$h \in {^{F_{\alpha }}2}$
. Note that the ordinal
![]() $\rho $
is
$\rho $
is
![]() $< \kappa $
. Inductively, we will construct a sequence
$< \kappa $
. Inductively, we will construct a sequence
![]() $\{r^{\alpha }_{l}:l<\rho \}$
of conditions below
$\{r^{\alpha }_{l}:l<\rho \}$
of conditions below
![]() $q_{\alpha }$
satisfying:
$q_{\alpha }$
satisfying:
-
(1)
 $r^{\alpha }_{0} = q_{\alpha }$
.
$r^{\alpha }_{0} = q_{\alpha }$
. -
(2)
 $r^{\alpha }_{l+1} \leq _{\alpha , F_{\alpha }} r^{\alpha }_{l}$
.
$r^{\alpha }_{l+1} \leq _{\alpha , F_{\alpha }} r^{\alpha }_{l}$
. -
(3)
 $(r^{\alpha }_{l+1})_{\bar {\sigma }_{l}}^{h_{l}} \Vdash \check {k}(\alpha ) \in \dot {X}$
.
$(r^{\alpha }_{l+1})_{\bar {\sigma }_{l}}^{h_{l}} \Vdash \check {k}(\alpha ) \in \dot {X}$
. -
(4) For l limit ordinal
 $r^{\alpha }_{l} = \bigwedge _{k< l} r^{\alpha }_{k}$
.
$r^{\alpha }_{l} = \bigwedge _{k< l} r^{\alpha }_{k}$
.
It is enough to explain how the successor step is built: Suppose then that we have constructed
![]() $r^{\alpha }_{l}$
satisfying the conditions above and consider the pair
$r^{\alpha }_{l}$
satisfying the conditions above and consider the pair
![]() $\gamma _{l} =(\bar {\sigma }, h)$
. Notice that since
$\gamma _{l} =(\bar {\sigma }, h)$
. Notice that since
![]() $\lvert F_{\alpha } \lvert < \kappa $
for all
$\lvert F_{\alpha } \lvert < \kappa $
for all
![]() $i \in F_{\alpha }$
,
$i \in F_{\alpha }$
,
![]() $\operatorname {\mathrm {split}}_{\alpha }(q_{\alpha }(i)) \subseteq \operatorname {\mathrm {split}}_{\delta }(p(i))$
for some
$\operatorname {\mathrm {split}}_{\alpha }(q_{\alpha }(i)) \subseteq \operatorname {\mathrm {split}}_{\delta }(p(i))$
for some
![]() $\delta \leq H(k(\alpha ))$
. Also, since
$\delta \leq H(k(\alpha ))$
. Also, since
![]() $f^{2}(k(\alpha )) < k(\alpha +1)$
and for all
$f^{2}(k(\alpha )) < k(\alpha +1)$
and for all
![]() $\bar {\tau } \in \Lambda _{f(\alpha )+1}^{F_{\alpha }}(p)$
we have that
$\bar {\tau } \in \Lambda _{f(\alpha )+1}^{F_{\alpha }}(p)$
we have that
![]() $C \backslash Y_{\bar {\tau }} \subseteq f(f(k(\alpha )))$
, we obtain that
$C \backslash Y_{\bar {\tau }} \subseteq f(f(k(\alpha )))$
, we obtain that
![]() $k(\alpha ) \in Y_{\bar {\tau }}$
for all
$k(\alpha ) \in Y_{\bar {\tau }}$
for all
![]() $\bar {\tau } \in \Lambda _{f(\alpha )+1}^{F_{\alpha }}(p)$
. Thus, again we repeat the argument above using the fact that p is preprocessed for
$\bar {\tau } \in \Lambda _{f(\alpha )+1}^{F_{\alpha }}(p)$
. Thus, again we repeat the argument above using the fact that p is preprocessed for
![]() $(\dot {X}, F_{\alpha })$
and find a set
$(\dot {X}, F_{\alpha })$
and find a set
![]() $F_{\alpha }^{\prime } \supseteq F_{\alpha }$
, a sequence
$F_{\alpha }^{\prime } \supseteq F_{\alpha }$
, a sequence
![]() $\bar {\tau }_{h} \in \Lambda ^{F_{\alpha }^{\prime }}_{\alpha }(p)$
, and conditions
$\bar {\tau }_{h} \in \Lambda ^{F_{\alpha }^{\prime }}_{\alpha }(p)$
, and conditions
![]() $w_{h}(\bar {\tau }_{h},k(\alpha )) \leq p^{h}_{\bar {\tau }_{h}}$
forcing
$w_{h}(\bar {\tau }_{h},k(\alpha )) \leq p^{h}_{\bar {\tau }_{h}}$
forcing
![]() $w_{h}(\bar {\tau }_{h},k(\alpha )) \Vdash k(\alpha ) \in \dot {X}$
. Moreover, we can choose
$w_{h}(\bar {\tau }_{h},k(\alpha )) \Vdash k(\alpha ) \in \dot {X}$
. Moreover, we can choose
![]() $w_{h}(\bar {\tau }_{h},k(\alpha ))$
so that
$w_{h}(\bar {\tau }_{h},k(\alpha ))$
so that
![]() $w_{h}(\bar {\tau }_{h},k(\alpha ))\leq (q_{\alpha })^{h}_{\bar {\tau }_{h}}$
. Note that
$w_{h}(\bar {\tau }_{h},k(\alpha ))\leq (q_{\alpha })^{h}_{\bar {\tau }_{h}}$
. Note that
![]() $w_{h}(\bar {\tau }_{h},k(\alpha ))$
might not yet be a condition satisfying the condition (2). In order to fix this, we define
$w_{h}(\bar {\tau }_{h},k(\alpha ))$
might not yet be a condition satisfying the condition (2). In order to fix this, we define
![]() $r^{\alpha }_{l+1}$
as follows:
$r^{\alpha }_{l+1}$
as follows:
![]() $\operatorname {\mathrm {supp}}(r^{\alpha }_{l+1})=\operatorname {\mathrm {supp}}(w_{l})$
and
$\operatorname {\mathrm {supp}}(r^{\alpha }_{l+1})=\operatorname {\mathrm {supp}}(w_{l})$
and
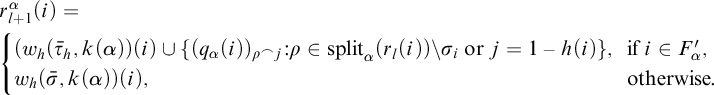 $$ \begin{align*} & r^{\alpha}_{l+1}(i) = \\ & \!\begin{cases} (w_{h}(\bar{\tau}_{h},k(\alpha))(i) \cup \{ (q_{\alpha}(i))_{\rho {}^{\frown} j}{:} \rho \in \operatorname{\mathrm{split}}_{\alpha} (r_{l}(i)) {\setminus} \sigma_{i} \text{ or } j= 1-h(i) \}, &\!\! \text{if } i \in F_{\alpha}^{\prime}, \\ w_{h}(\bar{\sigma},k(\alpha))(i), &\!\! \text{otherwise. } \end{cases} \end{align*} $$
$$ \begin{align*} & r^{\alpha}_{l+1}(i) = \\ & \!\begin{cases} (w_{h}(\bar{\tau}_{h},k(\alpha))(i) \cup \{ (q_{\alpha}(i))_{\rho {}^{\frown} j}{:} \rho \in \operatorname{\mathrm{split}}_{\alpha} (r_{l}(i)) {\setminus} \sigma_{i} \text{ or } j= 1-h(i) \}, &\!\! \text{if } i \in F_{\alpha}^{\prime}, \\ w_{h}(\bar{\sigma},k(\alpha))(i), &\!\! \text{otherwise. } \end{cases} \end{align*} $$
Finally, let
![]() $q_{\alpha +1}= \bigwedge _{l< \rho } r^{\alpha }_{l}$
,
$q_{\alpha +1}= \bigwedge _{l< \rho } r^{\alpha }_{l}$
,
![]() $\eta _{\alpha +1} = \eta _{\alpha } +1$
,
$\eta _{\alpha +1} = \eta _{\alpha } +1$
,
![]() $F_{\alpha +1}=F_{\alpha }^{\prime }\cup \{\min (\operatorname {\mathrm {supp}}(q_{\alpha +1})\backslash F_{\alpha }^{\prime })\}$
, and
$F_{\alpha +1}=F_{\alpha }^{\prime }\cup \{\min (\operatorname {\mathrm {supp}}(q_{\alpha +1})\backslash F_{\alpha }^{\prime })\}$
, and
![]() $g_{\alpha +1} = g_{\alpha } \cup \{(\min (\operatorname {\mathrm {supp}}(q_{\alpha +1})\backslash F_{\alpha }^{\prime }), \eta _{\alpha })\}$
. The construction is now complete. Indeed, to see that
$g_{\alpha +1} = g_{\alpha } \cup \{(\min (\operatorname {\mathrm {supp}}(q_{\alpha +1})\backslash F_{\alpha }^{\prime }), \eta _{\alpha })\}$
. The construction is now complete. Indeed, to see that
![]() $q_{\alpha +1} \Vdash \check {k}(\alpha ) \in \dot {X}$
notice that for all
$q_{\alpha +1} \Vdash \check {k}(\alpha ) \in \dot {X}$
notice that for all
![]() $\bar {\sigma } \in \Lambda ^{F_{\alpha }}_{\alpha }(q_{\alpha +1})$
and all
$\bar {\sigma } \in \Lambda ^{F_{\alpha }}_{\alpha }(q_{\alpha +1})$
and all
![]() $h \in {^{F_{\alpha }}} 2$
,
$h \in {^{F_{\alpha }}} 2$
,
![]() $(q_{\alpha +1})^{h}_{\bar {\sigma }} \Vdash \check {k}(\alpha ) \in \dot {X}$
.
$(q_{\alpha +1})^{h}_{\bar {\sigma }} \Vdash \check {k}(\alpha ) \in \dot {X}$
.
Remark 8.5. Note that
![]() $\kappa $
might cease to be measurable in
$\kappa $
might cease to be measurable in
![]() $V^{\mathbb {S}_{\kappa }^{\lambda }}$
from the above theorem. For a preparation of the universe, which guarantees that
$V^{\mathbb {S}_{\kappa }^{\lambda }}$
from the above theorem. For a preparation of the universe, which guarantees that
![]() $\kappa $
remains measurable see [Reference Friedman13].
$\kappa $
remains measurable see [Reference Friedman13].
9 Concluding remarks and questions
The use of the assumption
![]() $2^{\kappa }=\kappa ^{+}$
played a crucial role in our construction of a densely maximal
$2^{\kappa }=\kappa ^{+}$
played a crucial role in our construction of a densely maximal
![]() $\kappa $
-independent family. Thus one may ask:
$\kappa $
-independent family. Thus one may ask:
Question 9.1. Does ZFC imply the existence of a densely maximal
![]() $\kappa $
-independent families?
$\kappa $
-independent families?
Even though we are able to show both that consistently
![]() $\mathfrak {i}_{f}(\kappa )=\kappa ^{+} < 2^{\kappa }$
and
$\mathfrak {i}_{f}(\kappa )=\kappa ^{+} < 2^{\kappa }$
and
![]() $\kappa ^{+}<\mathfrak {i}_{f}(\kappa )=2^{\kappa }$
, the currently available techniques seem to be insufficient to answer the following:
$\kappa ^{+}<\mathfrak {i}_{f}(\kappa )=2^{\kappa }$
, the currently available techniques seem to be insufficient to answer the following:
Question 9.2. Let
![]() $\kappa $
be a regular uncountable cardinal. Is it consistent that
$\kappa $
be a regular uncountable cardinal. Is it consistent that
![]() $\kappa ^{+}<\mathfrak {i}(\kappa )<2^{\kappa }$
?
$\kappa ^{+}<\mathfrak {i}(\kappa )<2^{\kappa }$
?
The analogous question in the countable can be answered to the positive with the use of the so-called diagonalization filters (see [Reference Fischer and Shelah12]). A natural generalization of the notion of a diagonalization filter to the uncountable is given below:
Definition 9.3. Let
![]() $\mathcal {A}$
be a
$\mathcal {A}$
be a
![]() $\kappa $
-independent family. A
$\kappa $
-independent family. A
![]() $\kappa $
-complete filter
$\kappa $
-complete filter
![]() $\mathcal {F}$
is said to be a
$\mathcal {F}$
is said to be a
![]() $\kappa $
-diagonalization filter for
$\kappa $
-diagonalization filter for
![]() $\mathcal {A}$
if
$\mathcal {A}$
if
![]() $\forall F\in \mathcal {F}\forall h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})|F\cap \mathcal {A}^{h}|=\kappa $
and
$\forall F\in \mathcal {F}\forall h\in \operatorname {\mathrm {FF}}_{<\omega ,\kappa }(\mathcal {A})|F\cap \mathcal {A}^{h}|=\kappa $
and
![]() $\mathcal {F}$
is maximal with respect to the above property.
$\mathcal {F}$
is maximal with respect to the above property.
Moreover, as a straightforward generalization of the countable case (see [Reference Fischer and Shelah12]) one can show that:
Lemma 9.4 (See [Reference Fischer and Shelah12, Lemma 2]).
Suppose
![]() $\mathcal {A}$
is a
$\mathcal {A}$
is a
![]() $\kappa $
-independent family and
$\kappa $
-independent family and
![]() $\mathcal {F}$
is a
$\mathcal {F}$
is a
![]() $\kappa $
-diagonalization filter for
$\kappa $
-diagonalization filter for
![]() $\mathcal {A}$
. Let
$\mathcal {A}$
. Let
![]() $\mathbb {M}^{\kappa }_{\mathcal {F}}$
be the generalized Mathias forcing relativized to the filter
$\mathbb {M}^{\kappa }_{\mathcal {F}}$
be the generalized Mathias forcing relativized to the filter
![]() $\mathcal {F}$
.Footnote
8
Let G be an
$\mathcal {F}$
.Footnote
8
Let G be an
![]() $\mathbb {M}^{\kappa }_{\mathcal {F}}$
-generic filter and let
$\mathbb {M}^{\kappa }_{\mathcal {F}}$
-generic filter and let
![]() $x_{G}=\bigcup \{a:\exists A (a,A)\in G\}$
. Then
$x_{G}=\bigcup \{a:\exists A (a,A)\in G\}$
. Then
![]() $\mathcal {A}\cup \{x_{G}\}$
is
$\mathcal {A}\cup \{x_{G}\}$
is
![]() $\kappa $
-independent and moreover for each
$\kappa $
-independent and moreover for each
![]() $Y\in ([\kappa ]^{\kappa }\cap V)\backslash \mathcal {A}$
such that
$Y\in ([\kappa ]^{\kappa }\cap V)\backslash \mathcal {A}$
such that
![]() $\mathcal {A}\cup \{Y\}$
is
$\mathcal {A}\cup \{Y\}$
is
![]() $\kappa $
-independent, the family
$\kappa $
-independent, the family
![]() $\mathcal {A}\cup \{x_{G},Y\}$
is not
$\mathcal {A}\cup \{x_{G},Y\}$
is not
![]() $\kappa $
-independent.
$\kappa $
-independent.
Even though an appropriate iteration of posets of the above form would produce a positive answer to Question 9.2, the following remains open:
Question 9.5. Given a
![]() $\kappa $
-independent family
$\kappa $
-independent family
![]() $\mathcal {A}$
is there a
$\mathcal {A}$
is there a
![]() $\kappa $
-diagonalization filter for
$\kappa $
-diagonalization filter for
![]() $\mathcal {A}$
? The co-bounded filter does satisfy the characterization property in Definition 9.3; however, the requirement for maximality is not straightforward to satisfy. Is there a large cardinal property which guarantees the existence of such maximal filter? Note that a diagonalization filter is never an ultrafilter.
$\mathcal {A}$
? The co-bounded filter does satisfy the characterization property in Definition 9.3; however, the requirement for maximality is not straightforward to satisfy. Is there a large cardinal property which guarantees the existence of such maximal filter? Note that a diagonalization filter is never an ultrafilter.
Moreover of interest remain the following:
Question 9.6. Is it consistent that
![]() $\mathfrak {i}(\kappa )<\mathfrak {a}(\kappa )$
?
$\mathfrak {i}(\kappa )<\mathfrak {a}(\kappa )$
?
Clearly, if the above is consistent then in the corresponding model,
![]() $\mathfrak {i}(\kappa )\geq \kappa ^{++}$
. One of the original questions, which motivated the work on this project is the evaluation of
$\mathfrak {i}(\kappa )\geq \kappa ^{++}$
. One of the original questions, which motivated the work on this project is the evaluation of
![]() $\mathfrak {i}(\kappa )$
in the model from [Reference Brooke-Taylor, Fischer, Friedman and Montoya6]. More precisely, we would like to know:
$\mathfrak {i}(\kappa )$
in the model from [Reference Brooke-Taylor, Fischer, Friedman and Montoya6]. More precisely, we would like to know:
Question 9.7. Is it consistent that
![]() $\mathfrak {i}(\kappa ) < \mathfrak {u}(\kappa )?$
$\mathfrak {i}(\kappa ) < \mathfrak {u}(\kappa )?$
The consistency of
![]() $\mathfrak {r}<\mathfrak {i}$
holds in the Miller model. However, products of the generalized Miller poset
$\mathfrak {r}<\mathfrak {i}$
holds in the Miller model. However, products of the generalized Miller poset
![]() $\mathbb {MI}_{\kappa }^{\mathcal {U}}$
, where
$\mathbb {MI}_{\kappa }^{\mathcal {U}}$
, where
![]() $\mathcal {U}$
is a
$\mathcal {U}$
is a
![]() $\kappa $
-complete normal ultrafilter on
$\kappa $
-complete normal ultrafilter on
![]() $\kappa $
add
$\kappa $
add
![]() $\kappa $
-Cohen reals (see [Reference Brendle, Brooke-Taylor, Friedman and Montoya4, Theorem 85]) and so increase
$\kappa $
-Cohen reals (see [Reference Brendle, Brooke-Taylor, Friedman and Montoya4, Theorem 85]) and so increase
![]() $\mathfrak {r}(\kappa )$
. Even though
$\mathfrak {r}(\kappa )$
. Even though
![]() $\mathbb {MI}_{\kappa }^{\mathcal {U}}$
has the generalized Laver property (see [Reference Brendle, Brooke-Taylor, Friedman and Montoya4, Proposition 81]), it is open if the generalized Laver property is preserved under
$\mathbb {MI}_{\kappa }^{\mathcal {U}}$
has the generalized Laver property (see [Reference Brendle, Brooke-Taylor, Friedman and Montoya4, Proposition 81]), it is open if the generalized Laver property is preserved under
![]() $\kappa $
-support iterations. This leaves us with the following:
$\kappa $
-support iterations. This leaves us with the following:
Question 9.8. Is it consistent that
![]() $\mathfrak {r}(\kappa )<\mathfrak {i}(\kappa )$
?
$\mathfrak {r}(\kappa )<\mathfrak {i}(\kappa )$
?
10 Appendix: strong independence
Another approach towards finding a higher analogues of independence for a given uncountable cardinal
![]() $\kappa $
is to consider Boolean combinations generated by strictly less than
$\kappa $
is to consider Boolean combinations generated by strictly less than
![]() $\kappa $
(not just finitely) many members of the family. More precisely one can give the following definition:
$\kappa $
(not just finitely) many members of the family. More precisely one can give the following definition:
Definition 10.1. Let
![]() $\kappa $
be a regular uncountable cardinal,
$\kappa $
be a regular uncountable cardinal,
![]() $\mathcal {A}\subseteq [\kappa ]^{\kappa }$
of cardinality at least
$\mathcal {A}\subseteq [\kappa ]^{\kappa }$
of cardinality at least
![]() $\kappa $
.
$\kappa $
.
-
(1) Let
 $\operatorname {\mathrm {FF}}_{<\kappa ,\kappa }(\mathcal {A})$
be the set of partial functions
$\operatorname {\mathrm {FF}}_{<\kappa ,\kappa }(\mathcal {A})$
be the set of partial functions
 $h:\mathcal {A}\to \{0,1\}$
with domain of cardinality strictly below
$h:\mathcal {A}\to \{0,1\}$
with domain of cardinality strictly below
 $\kappa $
and for
$\kappa $
and for
 $h\in \operatorname {\mathrm {FF}}_{<\kappa ,\kappa }(\mathcal {A})$
let
$h\in \operatorname {\mathrm {FF}}_{<\kappa ,\kappa }(\mathcal {A})$
let
 $\mathcal {A}^{h}=\bigcap \{\mathcal {A}^{h(A)}: A\in \operatorname {\mathrm {dom}}(h)\}$
where
$\mathcal {A}^{h}=\bigcap \{\mathcal {A}^{h(A)}: A\in \operatorname {\mathrm {dom}}(h)\}$
where
 $\mathcal {A}^{h(A)}=A$
if
$\mathcal {A}^{h(A)}=A$
if
 $h(A)=0$
and
$h(A)=0$
and
 $\mathcal {A}^{h(A)}=\kappa \backslash A$
if
$\mathcal {A}^{h(A)}=\kappa \backslash A$
if
 $h(A)=1$
.
$h(A)=1$
. -
(2) The family
 $\mathcal {A}$
is said to be strongly
$\mathcal {A}$
is said to be strongly
 $\kappa $
-independent if for every
$\kappa $
-independent if for every
 $h\in \operatorname {\mathrm {FF}}_{<\kappa ,\kappa }(\mathcal {A})$
the Boolean combination
$h\in \operatorname {\mathrm {FF}}_{<\kappa ,\kappa }(\mathcal {A})$
the Boolean combination
 $\mathcal {A}^{h}$
is unbounded.
$\mathcal {A}^{h}$
is unbounded. -
(3) The family
 $\mathcal {A}$
is said to be maximal strongly
$\mathcal {A}$
is said to be maximal strongly
 $\kappa $
-independent if it is strongly
$\kappa $
-independent if it is strongly
 $\kappa $
-independent and is not properly contained in another strongly
$\kappa $
-independent and is not properly contained in another strongly
 $\kappa $
-independent family.
$\kappa $
-independent family. -
(4) Suppose
 $\kappa $
is a regular uncountable cardinal for which maximal strongly
$\kappa $
is a regular uncountable cardinal for which maximal strongly
 $\kappa $
-independent families exist. With
$\kappa $
-independent families exist. With
 $\mathfrak {i}_{s}(\kappa )$
we denote the minimal size of a maximal strongly
$\mathfrak {i}_{s}(\kappa )$
we denote the minimal size of a maximal strongly
 $\kappa $
-independent family.
$\kappa $
-independent family.
Note that the increasing union of a countable sequence of strongly
![]() $\kappa $
-independent families is not necessarily strongly
$\kappa $
-independent families is not necessarily strongly
![]() $\kappa $
-independent. Thus one cannot apply Zorn’s lemma to claim the existence of maximal strongly
$\kappa $
-independent. Thus one cannot apply Zorn’s lemma to claim the existence of maximal strongly
![]() $\kappa $
-independent families. What we can say is the following:
$\kappa $
-independent families. What we can say is the following:
Theorem 10.2. Let
![]() $\kappa $
be a regular uncountable cardinal.
$\kappa $
be a regular uncountable cardinal.
-
(1) For
 $\kappa $
strongly inaccessible, there is a strongly
$\kappa $
strongly inaccessible, there is a strongly
 $\kappa $
-independent family of cardinality
$\kappa $
-independent family of cardinality
 $2^{\kappa }$
.
$2^{\kappa }$
. -
(2) If
 $\mathcal {A}$
is strongly
$\mathcal {A}$
is strongly
 $\kappa $
-independent and
$\kappa $
-independent and
 $|\mathcal {A}|<\mathfrak {r}(\kappa )$
then
$|\mathcal {A}|<\mathfrak {r}(\kappa )$
then
 $\mathcal {A}$
is not maximal.
$\mathcal {A}$
is not maximal. -
(3) Suppose
 $\mathfrak {d}(\kappa )$
is such that for every
$\mathfrak {d}(\kappa )$
is such that for every
 $\gamma <\mathfrak {d}(\kappa )$
,
$\gamma <\mathfrak {d}(\kappa )$
,
 $\gamma ^{<\kappa }<\mathfrak {d}(\kappa )$
. If
$\gamma ^{<\kappa }<\mathfrak {d}(\kappa )$
. If
 $\mathcal {A}$
is strongly
$\mathcal {A}$
is strongly
 $\kappa $
-independent and
$\kappa $
-independent and
 $|\mathcal {A}|<\mathfrak {d}(\kappa )$
then
$|\mathcal {A}|<\mathfrak {d}(\kappa )$
then
 $\mathcal {A}$
is not maximal.
$\mathcal {A}$
is not maximal.
Proof We will prove
![]() $(1)$
. Let
$(1)$
. Let
![]() $\mathcal {C}=\{(\gamma , A): \gamma <\kappa , A\subseteq \mathcal {P}(\gamma )\}$
. Given
$\mathcal {C}=\{(\gamma , A): \gamma <\kappa , A\subseteq \mathcal {P}(\gamma )\}$
. Given
![]() $X\subseteq \kappa $
define
$X\subseteq \kappa $
define
![]() $\mathcal {Y}_{X}=\{(\gamma , A)\in \mathcal {C}: X\cap \gamma \in A\}$
. Then
$\mathcal {Y}_{X}=\{(\gamma , A)\in \mathcal {C}: X\cap \gamma \in A\}$
. Then
![]() $\mathcal {Y}_{X}: X\subseteq \kappa \}$
is strongly
$\mathcal {Y}_{X}: X\subseteq \kappa \}$
is strongly
![]() $\kappa $
-independent. Indeed. Consider two disjoint subfamilies of
$\kappa $
-independent. Indeed. Consider two disjoint subfamilies of
![]() $[\kappa ]^{\kappa }$
, each of size strictly smaller than
$[\kappa ]^{\kappa }$
, each of size strictly smaller than
![]() $\kappa $
, say
$\kappa $
, say
![]() $\{X_{i}\}_{i\in I_{1}}$
and
$\{X_{i}\}_{i\in I_{1}}$
and
![]() $\{Z_{j}\}_{j\in I_{2}}$
. Note that
$\{Z_{j}\}_{j\in I_{2}}$
. Note that
![]() $(\gamma , A)\in \mathcal {X}=\bigcap _{i\in I_{1}} \mathcal {Y}_{X_{i}}\cap \bigcap _{j\in I_{2}}(\mathcal {C}\backslash \mathcal {Y}_{Z_{j}})$
if for all
$(\gamma , A)\in \mathcal {X}=\bigcap _{i\in I_{1}} \mathcal {Y}_{X_{i}}\cap \bigcap _{j\in I_{2}}(\mathcal {C}\backslash \mathcal {Y}_{Z_{j}})$
if for all
![]() $i\in I_{1}$
,
$i\in I_{1}$
,
![]() $X_{i}\cap A\in A$
and for all
$X_{i}\cap A\in A$
and for all
![]() $j\in I_{2}$
,
$j\in I_{2}$
,
![]() $Z_{j}\cap \gamma \notin A$
. However, there are unboundedly many
$Z_{j}\cap \gamma \notin A$
. However, there are unboundedly many
![]() $\gamma \in \kappa $
such that:
$\gamma \in \kappa $
such that:
-
•
 $X_{i}\cap \gamma \neq X_{i^{\prime }}\cap \gamma $
for
$X_{i}\cap \gamma \neq X_{i^{\prime }}\cap \gamma $
for
 $i\neq i^{\prime }$
both in
$i\neq i^{\prime }$
both in
 $I_{1}$
,
$I_{1}$
, -
•
 $Z_{j}\cap \gamma \neq Z_{j^{\prime }}\cap \gamma $
for
$Z_{j}\cap \gamma \neq Z_{j^{\prime }}\cap \gamma $
for
 $j\neq j^{\prime }$
both in
$j\neq j^{\prime }$
both in
 $I_{2}$
, and
$I_{2}$
, and -
•
 $X_{i}\cap \gamma \neq Z_{j}\cap \gamma $
for all
$X_{i}\cap \gamma \neq Z_{j}\cap \gamma $
for all
 $i\in I_{1}$
,
$i\in I_{1}$
,
 $j\in I_{2}$
.
$j\in I_{2}$
.
It remains to observe that for each such
![]() $\gamma $
, we have
$\gamma $
, we have
![]() $(\gamma , A_{\gamma })\in \mathcal {X}$
, where
$(\gamma , A_{\gamma })\in \mathcal {X}$
, where
![]() $A_{\gamma }=\{X_{i}\cap \gamma :i\in I_{1}\}$
.
$A_{\gamma }=\{X_{i}\cap \gamma :i\in I_{1}\}$
.
To see part
![]() $(2)$
note that if
$(2)$
note that if
![]() $|\mathcal {A}|<\mathfrak {r}(\kappa )$
, then the set
$|\mathcal {A}|<\mathfrak {r}(\kappa )$
, then the set
![]() $\{\mathcal {A}^{h}:h\in \operatorname {\mathrm {FF}}_{<\kappa ,\kappa }(\mathcal {A})\}$
is split by some
$\{\mathcal {A}^{h}:h\in \operatorname {\mathrm {FF}}_{<\kappa ,\kappa }(\mathcal {A})\}$
is split by some
![]() $X\in [\kappa ]^{\kappa }$
and so
$X\in [\kappa ]^{\kappa }$
and so
![]() $\mathcal {A}\cup \{X\}$
is strongly
$\mathcal {A}\cup \{X\}$
is strongly
![]() $\kappa $
-independent which properly contains
$\kappa $
-independent which properly contains
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
For a proof of part
![]() $(3)$
, see [Reference Brooke-Taylor, Fischer, Friedman and Montoya6, Proposition 27].
$(3)$
, see [Reference Brooke-Taylor, Fischer, Friedman and Montoya6, Proposition 27].
Corollary 10.3. Thus, if
![]() $\mathfrak {i}_{s}(\kappa )$
is defined, then
$\mathfrak {i}_{s}(\kappa )$
is defined, then
![]() $\kappa ^{+}\leq \mathfrak {i}_{s}(\kappa )\leq 2^{\kappa }$
. Moreover
$\kappa ^{+}\leq \mathfrak {i}_{s}(\kappa )\leq 2^{\kappa }$
. Moreover
![]() $\mathfrak {r}(\kappa )\leq \mathfrak {i}_{s}(\kappa )$
and if for every
$\mathfrak {r}(\kappa )\leq \mathfrak {i}_{s}(\kappa )$
and if for every
![]() $\gamma <\mathfrak {d}(\kappa )$
,
$\gamma <\mathfrak {d}(\kappa )$
,
![]() $\gamma ^{<\kappa }<\mathfrak {d}(\kappa )$
, then
$\gamma ^{<\kappa }<\mathfrak {d}(\kappa )$
, then
![]() $\mathfrak {d}(\kappa )\leq \mathfrak {i}_{s}(\kappa )$
.
$\mathfrak {d}(\kappa )\leq \mathfrak {i}_{s}(\kappa )$
.
Question 10.4.
-
(1) Is there a large cardinal property which implies the existence of a maximal strongly
 $\kappa $
-independent family?
$\kappa $
-independent family? -
(2) Given a strongly
 $\kappa $
-independent family
$\kappa $
-independent family
 $\mathcal {A}$
, is there a large cardinal property which implies the existence of a
$\mathcal {A}$
, is there a large cardinal property which implies the existence of a
 $\kappa $
-diagonalization filter for
$\kappa $
-diagonalization filter for
 $\mathcal {A}$
?
$\mathcal {A}$
? -
(3) Suppose
 $\mathfrak {i}_{s}(\kappa )$
is defined. A family which is strongly
$\mathfrak {i}_{s}(\kappa )$
is defined. A family which is strongly
 $\kappa $
-independent is
$\kappa $
-independent is
 $\kappa $
-independent. However a maximal strongly independent family is not necessarily maximal independent. Is there a ZFC relation between
$\kappa $
-independent. However a maximal strongly independent family is not necessarily maximal independent. Is there a ZFC relation between
 $\mathfrak {i}_{s}(\kappa )$
and
$\mathfrak {i}_{s}(\kappa )$
and
 $\mathfrak {i}(\kappa )$
?
$\mathfrak {i}(\kappa )$
?
Acknowledgements
The authors would like to thank the anonymous referee for many helpful comments which significantly improved the quality of the manuscript. The authors would also like to thank the Austrian Science Fund (FWF) for the generous support through Grant Y1012-N35, as well as I4039 (Fischer) and T1100 (Montoya).