Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T17:28:26.441Z Has data issue: false hasContentIssue false
  • English
  • Français

Hybrid logics: characterization, interpolation and complexity

Published online by Cambridge University Press:  12 March 2014

Carlos Areces ,
Patrick Blackburn  and
Maarten Marx
Carlos Areces
Affiliation:
ILLC, University of Amsterdam, Plantage Muidergracht 24, 1018TV, Amsterdam, The Netherlands, E-mail: carlos@science.uva.nl
Patrick Blackburn
Affiliation:
INRIA, Lorraine, 615, Rue du Jardin Botanique, 54602 Villers lès Nancy Cedex, France, E-mail: patrick@aplog.org
Maarten Marx
Affiliation:
Department of Sociology and Anthropology, University of Amsterdam, Plantage Muidergracht 24, 1018TV, Amsterdam, The Netherlands, E-mail: marx@science.uva.nl
Get access Rights & Permissions [Opens in a new window]

Abstract

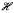Hybrid languages are expansions of propositional modal languages which can refer to (or even quantify over) worlds. The use of strong hybrid languages dates back to at least [Pri67], but recent work (for example [BS98, BT98a, BT99]) has focussed on a more constrained system called H(↓, @). We show in detail that (↓, @) is modally natural. We begin by studying its expressivity, and provide model theoretic characterizations (via a restricted notion of Ehrenfeucht-Fraïssé game, and an enriched notion of bisimulation) and a syntactic characterization (in terms of bounded formulas). The key result to emerge is that 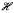(↓, @) corresponds to the fragment of first-order logic which is invariant for generated submodels. We then show that 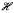(↓, @) enjoys (strong) interpolation, provide counterexamples for its finite variable fragments, and show that weak interpolation holds for the sublanguage 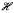(@). Finally, we provide complexity results for 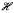(@) and other fragments and variants, and sharpen known undecidability results for (↓, @).

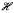Type
Research Article
Information
The Journal of Symbolic Logic , Volume 66 , Issue 3 , September 2001 , pp. 977 - 1010
Copyright
Copyright © Association for Symbolic Logic 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[ABM99]Areces, C., Blackburn, P., and Marx, M., A roadmap of the complexity of hybrid logics, Computer science logic (Flum, J. and Rodríguez-Artalejo, M., editors), LNCS, no. 1683, Springer, 1999, Proceedings of the 8th Annual Conference of the EACSL, Madrid, 09 1999, pp. 307–321.CrossRefGoogle Scholar
[ABM00]Areces, C., Blackburn, P., and Marx, M., The computational complexity of hybrid temporal logics, Logic Journal of the IGPL, vol. 8 (2000), no. 5, pp. 653–679.CrossRefGoogle Scholar
[Bet53]Beth, E., On Padoa's method in the theory of definition, Nederl. Akad. Wetensch. Proc. Ser. A. 56 = Indagationes Math., vol. 15 (1953), pp. 330–339.CrossRefGoogle Scholar
[Bla93]Blackburn, P., Nominal tense logic, Notre Dame Journal of Formal Logic, vol. 34 (1993), no. 1, pp. 56–83.Google Scholar
[Bla00]Blackburn, P., Internalizing labelled deduction, Journal of Logic and Computation, vol. 10 (2000), no. 1, pp. 136–168.CrossRefGoogle Scholar
[BS95]Blackburn, P. and Seligman, J., Hybrid languages, Journal of Logic, Language and Information, vol. 4 (1995), no. 3, pp. 251–272. Special issue on decompositions of first-order logic.CrossRefGoogle Scholar
[BS98]Blackburn, P. and Seligman, J., What are hybrid languages?, Advances in modal logic (Kracht, M., de Rijke, M., Wansing, H., and Zakharyaschev, M., editors), vol. 1, CSLI Publications, Stanford University, 1998, pp. 41–62.Google Scholar
[BT98a]Blackburn, P. and Tzakova, M., Hybrid completeness, Logic Journal of the IGPL, vol. 6 (1998), no. 4, pp. 625–650.CrossRefGoogle Scholar
[BT98b]Blackburn, P. and Tzakova, M., Hybrid languages and temporal logics (full version), Technical Report CLAUS-Report 96, Computerlinguistik, Universität des Saarlandes, 1998, http://www.coli.uni-sb.de/cl/claus.Google Scholar
[BT99]Blackburn, P. and Tzakova, M., Hybrid languages and temporal logics, Logic Journal of the IGPL, vol. 7 (1999), no. 1, pp. 27–54.CrossRefGoogle Scholar
[Bul70]Bull, R., An approach to tense logic, Theoria, vol. 36 (1970), pp. 282–300.CrossRefGoogle Scholar
[CK90]Chang, C. and Keisler, H., Model theory, third ed., Studies in Logic and the Foundations of Mathematics, vol. 73, North-Holland Publishing Co, Amsterdam, 1990.Google Scholar
[Com85]Comrie, B., Tense, Cambridge University Press, 1985.CrossRefGoogle Scholar
[Cra57]Craig, W., Three uses of the Herbrand-Gentzen theorem in relating model theory and proof theory, this Journal, vol. 22 (1957), pp. 269–285.Google Scholar
[Cze82]Czelakowski, J., Logical matrices and the amalgamation property, Studia Logica, vol. XLI (1982), no. 4, pp. 329–341.CrossRefGoogle Scholar
[De95]De Giacomo, G., Decidability of class-based knowledge representation formalisms, Ph.D. thesis, Università di Roma “La Sapienza”, 1995.Google Scholar
[End72]Enderton, H., A mathematical introduction to logic, Academic Press, New York, 1972.Google Scholar
[GG93]Gargov, G. and Goranko, V., Modal logic with names, Journal of Philosophical Logic, vol. 22 (1993), no. 6, pp. 607–636.CrossRefGoogle Scholar
[Gor96]Goranko, V., Hierarchies of modal and temporal logics with reference pointers, Journal of Logic, Language and Information, vol. 5 (1996), no. 1, pp. 1–24.CrossRefGoogle Scholar
[HM92]Halpern, J. and Moses, Y., A guide to completeness and complexity for modal logics of knowledge and belief, Artificial Intelligence, vol. 54 (1992), pp. 319–379.CrossRefGoogle Scholar
[Hod93]Hodges, W., Model theory, Cambridge University Press, Cambridge, 1993.CrossRefGoogle Scholar
[Lad77]Ladner, R., The computational complexity of provability in systems of modal propositional logic, SIAM Journal of Computing, vol. 6 (1977), no. 3, pp. 467–480.CrossRefGoogle Scholar
[Mak91]Maksimova, L., Amalgamation and interpolation in normal modal logics, Studia Logica, vol. L (1991), no. 3/4, pp. 457–471.CrossRefGoogle Scholar
[MV97]Marx, M. and Venema, Y., Multi-dimensional modal logic, Applied Logic Series, Kluwer Academic Publishers, 1997.CrossRefGoogle Scholar
[Pap94]Papadimitriou, C., Computational complexity, Addison-Wesley, 1994.Google Scholar
[PT85]Passy, S. and Tinchev, T., Quantifiers in combinatory PDL: completeness, definability, incompleteness, Fundamentals of computation theory (Cottbus, 1985), Springer, Berlin, 1985, pp. 512–519.CrossRefGoogle Scholar
[PT91]Passy, S. and Tinchev, T., An essay in combinatory dynamic logic, Information and Computation, vol. 93 (1991), no. 2, pp. 263–332.CrossRefGoogle Scholar
[Pri67]Prior, A., Past, present and future, Clarendon Press, Oxford, 1967.CrossRefGoogle Scholar
[Rei47]Reichenbach, H., Elements of symbolic logic, Random House, New York, 1947.Google Scholar
[Sel91]Seligman, J., A cut-free sequent calculus for elementary situated reasoning, Technical Report HCRC/RP-22, HCRC, Edinburgh, 1991.Google Scholar
[Sel97]Seligman, J., The logic of correct description, Advances in intensional logic (de Rijke, M., editor), Kluwer, 1997, pp. 107–135.CrossRefGoogle Scholar
[Spa93a]Spaan, E., Complexity of modal logics, Ph.D. thesis, ILLC, University of Amsterdam, 1993.Google Scholar
[Spa93b]Spaan, E., The complexity of propositional tense logics, Diamonds and defaults (Amsterdam, 1990/1991), Kluwer Acad. Publ., Dordrecht, 1993, pp. 287–307.CrossRefGoogle Scholar
[Tza99]Tzakova, M., Tableaux calculi for hybrid logics., Conference on tableaux calculi and related methods (TABLEAUX), Saratoga Springs, USA (Murray, N., editor), LNAI, vol. 1617, Springer Verlag, 1999, pp. 278–292.Google Scholar
[vB83]van Benthem, J., Modal logic and classical logic, Bibliopolis, Naples, 1983.Google Scholar
[vB96]van Benthem, J., Exploring logical dynamics, Studies in Logic, Language and Information, CSLI Publications, Stanford, 1996.Google Scholar
[Ven94]Venema, Y., A modal logic for quantification and substitution, Bulletin of the IGPL, vol. 2 (1994), no. 1, pp. 31–45.CrossRefGoogle Scholar
[Woo81]Woods, A., Some problems in logic and number theory, and their connections, Ph.D. thesis, University of Manchester, 1981.Google Scholar