Article contents
The hypothesis that infinite classes are similar
Published online by Cambridge University Press: 12 March 2014
Extract
Let “the hypothesis of similarity” be the hypothesis that all infinite classes are similar (have the same power or cardinal number). It will be shown that the system of logic of Whitehead and Russell's Principia mathematica (without the axiom of reducibility) is consistent when to its axioms are added all the following:
(1). The hypothesis of similarity.
(2). The axiom of infinity.
(3). The axiom of choice.
(4). The contradictory of the axiom of reducibility.
If (2) – (4) but not (1) are employed in Principia, it must therefore be the case that Cantor's theorem is not deducible, since it contradicts (1). If (2) and (3) but not (1) and (4) are employed, then a proof of Cantor's theorem must require the use of some sort of reducibility principle.
The first step in the required consistency proof is to modify in certain respects the system S of a previous paper. Immediately after definition 3.5 the following definition is to be added:
3.5.1. If a is of the form 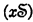 (b,c), where x is an S-variable and where b and c are S-constants neither of which is of higher order than that of x, then a is an S-proposition.
(b,c), where x is an S-variable and where b and c are S-constants neither of which is of higher order than that of x, then a is an S-proposition.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1939
References
1 This hypothesis is equivalent to Chwistek's “axiom of enumerability” according to which every infinite class is enumerable. See his paper, Über die Hypothesen der Mengenlehre, Mathematische Zeitschrift, vol. 25 (1926), pp. 439–473CrossRefGoogle Scholar, in the last paragraph of which he points out that the axiom of enumerability can be employed in each type provided that the ramified theory of types (without the axiom of reducibility) is used. The hypothesis of similarity (or the equivalent axiom of enumerability) is clearly a stronger assumption than the axiom of choice, since enumeration presupposes well-ordering.
2 By “Cantor's theorem” is here meant the well-known theorem of the theory of aggregates that every class has a greater number of subclasses than it has members. Of course it is not possible meaningfully to express Cantor's theorem in its full generality if the ramified theory of types is employed, because the concept of “subclass” must be limited to “subclass of order ν,” where ν is specified. The use of the axiom of reducibility, however, makes possible an adequate statement and proof of Cantor's theorem, as well as appearing to be a prerequisite for proving that every bounded sequence of real numbers has a least upper bound.
3 Fitch, F. B., The consistency of the ramified Principia, this Journal vol. 3 (1938), pp. 140–149Google Scholar. Definitions and theorems in the above paper will be referred to by number in the present paper. See also review of the above by Bernays, Paul, The consistency of the ramified Principia, this Journal vol. 4 (1939), pp. 97–98Google Scholar. The schemata suggested by Bernays constitute an interesting improvement on the system S; I have since seen a proof by Bernays that 4.4.11 can be deduced in S on the basis of the new schemata. The following correction should be made in The consistency of the ramified Principia: Add to the first sentence of 3.7 the words “and suppose that b and c are of the same type, in the sense of 3.10.”
- 4
- Cited by

