Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Asperó, David
and
Schindler, Ralf
2014.
Bounded Martin’s Maximum with an Asterisk.
Notre Dame Journal of Formal Logic,
Vol. 55,
Issue. 3,
Fuchs, Gunter
2024.
Errata: on the role of the continuum hypothesis in forcing principles for subcomplete forcing.
Archive for Mathematical Logic,
Vol. 63,
Issue. 5-6,
p.
509.

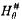 exists, then there is a stationary set preserving forcing which increases
exists, then there is a stationary set preserving forcing which increases 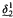 . Moreover, if Bounded Martin's Maximum holds and the nonstationary ideal on
. Moreover, if Bounded Martin's Maximum holds and the nonstationary ideal on 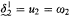 .
.