Article contents
The independence of Quine's axioms *200 and *201
Published online by Cambridge University Press: 12 March 2014
Extract
We refer to the axioms in Quine's book, Mathematical logic, New York, 1940.
To prove the independence of *200, give xϵ α the truth value F in all cases and give (x)ϕ the same truth value as ϕ. Then clearly all formulas derivable from the other axioms besides *200 have the value T, whereas from *200 one can derive (∃x)(∃α)(xϵ α) which has the value F. This method of proving independence amounts to taking for a model a universe consisting of the single object Λ.
For *201 we prove a contingent independence. That is, we prove that if Quine's system is consistent, then *201 is independent. The line of argument is the following. Suppose *201 can be derived from the other axioms. Let us replace xϵ α by 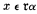 throughout all the axioms. Then what *201 becomes can be derived from what the other axioms become. However what *201 becomes will lead to a contradiction in Quine's system whereas the rules which the other axioms become are valid in Quine's system.
throughout all the axioms. Then what *201 becomes can be derived from what the other axioms become. However what *201 becomes will lead to a contradiction in Quine's system whereas the rules which the other axioms become are valid in Quine's system.
We now get down to technical details. Let us refer to the replacement of xϵ α by 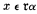 throughout an expression as an r replacement. Denote the result of performing an r replacement on ϕ by ϕr. Let Wα denote
throughout an expression as an r replacement. Denote the result of performing an r replacement on ϕ by ϕr. Let Wα denote
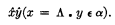
Then

Note that if x and y are variables, then by D10,
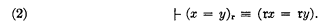
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1941
- 1
- Cited by

