Article contents
Independence proofs in predicate logic with infinitely long expressions
Published online by Cambridge University Press: 12 March 2014
Extract
The systems of predicate logic considered here are extensions of ordinary first-order predicate logic. They were obtained by first admitting infinite conjunctions, disjunctions, and quantifications into formulas, and then adjusting the axiom schemata and rules of inference to accommodate them. In this paper, only systems with formulas of denumerable length and “formal proofs” with denumerably many steps will be discussed, though such restrictions are hardly essential. The systems 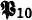 with denumerable conjunctions and disjunctions, but finite quantifications, are semantically complete; i.e., valid formulas are provable. However, systems
with denumerable conjunctions and disjunctions, but finite quantifications, are semantically complete; i.e., valid formulas are provable. However, systems 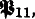 in which denumerably infinite quantifications are also allowed, are semantically incomplete.
in which denumerably infinite quantifications are also allowed, are semantically incomplete.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1962
References
- 3
- Cited by

