Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T18:02:47.732Z Has data issue: false hasContentIssue false
  • English
  • Français

Independent axiom schemata for S5

Published online by Cambridge University Press:  12 March 2014

Alan Ross Anderson
Alan Ross Anderson*
Affiliation:
Yale University
Get access Rights & Permissions [Opens in a new window]

Extract

Leo Simons has shown that H1—H6 below constitute a set of independent axiom schemata for S3, with detachment for material implication “→” as the only primitive rule. He also showed that addition of the scheme (◇ ◇ α ⥽ ◇ α) yields S4, and that these schemata for S4 are independent. The question for S5 was left open. We shall show (presupposing familiarity with Simons' paper) that H1—H6 and S, below, constitute a set of independent axiom schemata for S5, with detachment for material implication as the only primitive rule.

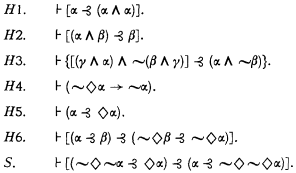
Let S5′ be the system generated from H1—H6 and S with the help of the primitive rule. It is easy to see that Simons' derivations of the rules (a) adjunction, (b) detachment for strict implication, and (c) intersubstitutability of strict equivalents, may be carried out for S5′. We know that (1) (∼ ◇ ∼ α ⥽ ◇ α) is provable in S2, hence also in S3 and S5′; and (1) and S yield (2) (α ⥽ ∼ ◇ ∼ ◇ α). Perry has shown that addition of (2) to S3 yields S5, so S5 is a subsystem of S5′. And it is easy to prove S in S5; hence the systems are equivalent.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 21 , Issue 3 , September 1956 , pp. 255 - 256
Copyright
Copyright © Association for Symbolic Logic 1956

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 New axiomatizations of S3 and S4, this Journal, vol. 18 (1953), pp. 309–316Google Scholar. We adopt Simons' notational conventions.

2 The systems S3, S4, and S5 are described in Lewis, C. I. and Langford, C. H., Symbolic Logic, New York, 1932, pp. 500–501Google Scholar.

3 See especially Simons' Theorems 1, 28, and 29, loc. cit.

4 See Theorem 18.43 (p. 164) and p. 500 of Lewis and Langford, op. cit.

5 Parry, W. T., Modalities in the survey system of strict implication, this Journal, vol. 4 (1939), pp. 137–154. See especially pp. 151–152Google Scholar.

6 See Lewis and Langford, op. cit., p. 498, item (8).