Article contents
INDESTRUCTIBILITY OF THE TREE PROPERTY
Published online by Cambridge University Press: 16 September 2019
Abstract
In the first part of the article, we show that if 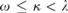 $\omega \le \kappa < \lambda$ are cardinals,
$\omega \le \kappa < \lambda$ are cardinals, 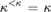 ${\kappa ^{ < \kappa }} = \kappa$, and λ is weakly compact, then in
${\kappa ^{ < \kappa }} = \kappa$, and λ is weakly compact, then in 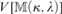 $V\left[M {\left( {\kappa ,\lambda } \right)} \right]$ the tree property at
$V\left[M {\left( {\kappa ,\lambda } \right)} \right]$ the tree property at 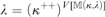 $$\lambda= \left( {\kappa ^{ ++ } } \right)^{V\left[ {\left( {\kappa ,\lambda } \right)} \right]} $$ is indestructible under all
$$\lambda= \left( {\kappa ^{ ++ } } \right)^{V\left[ {\left( {\kappa ,\lambda } \right)} \right]} $$ is indestructible under all 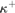 ${\kappa ^ + }$-cc forcing notions which live in
${\kappa ^ + }$-cc forcing notions which live in 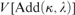 $V\left[ {{\rm{Add}}\left( {\kappa ,\lambda } \right)} \right]$, where
$V\left[ {{\rm{Add}}\left( {\kappa ,\lambda } \right)} \right]$, where 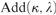 ${\rm{Add}}\left( {\kappa ,\lambda } \right)$ is the Cohen forcing for adding λ-many subsets of κ and
${\rm{Add}}\left( {\kappa ,\lambda } \right)$ is the Cohen forcing for adding λ-many subsets of κ and 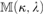 $\left( {\kappa ,\lambda } \right)$ is the standard Mitchell forcing for obtaining the tree property at
$\left( {\kappa ,\lambda } \right)$ is the standard Mitchell forcing for obtaining the tree property at 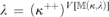 $\lambda= \left( {\kappa ^{ ++ } } \right)^{V\left[ {\left( {\kappa ,\lambda } \right)} \right]} $. This result has direct applications to Prikry-type forcing notions and generalized cardinal invariants. In the second part, we assume that λ is supercompact and generalize the construction and obtain a model
$\lambda= \left( {\kappa ^{ ++ } } \right)^{V\left[ {\left( {\kappa ,\lambda } \right)} \right]} $. This result has direct applications to Prikry-type forcing notions and generalized cardinal invariants. In the second part, we assume that λ is supercompact and generalize the construction and obtain a model 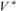 ${V^{\rm{*}}}$, a generic extension of V, in which the tree property at
${V^{\rm{*}}}$, a generic extension of V, in which the tree property at 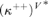 ${\left( {{\kappa ^{ + + }}} \right)^{{V^{\rm{*}}}}}$ is indestructible under all
${\left( {{\kappa ^{ + + }}} \right)^{{V^{\rm{*}}}}}$ is indestructible under all 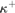 ${\kappa ^ + }$-cc forcing notions living in
${\kappa ^ + }$-cc forcing notions living in 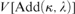 $V\left[ {{\rm{Add}}\left( {\kappa ,\lambda } \right)} \right]$, and in addition under all forcing notions living in
$V\left[ {{\rm{Add}}\left( {\kappa ,\lambda } \right)} \right]$, and in addition under all forcing notions living in 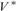 ${V^{\rm{*}}}$ which are
${V^{\rm{*}}}$ which are 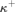 ${\kappa ^ + }$-closed and “liftable” in a prescribed sense (such as
${\kappa ^ + }$-closed and “liftable” in a prescribed sense (such as 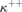 ${\kappa ^{ + + }}$-directed closed forcings or well-met forcings which are
${\kappa ^{ + + }}$-directed closed forcings or well-met forcings which are 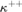 ${\kappa ^{ + + }}$-closed with the greatest lower bounds).
${\kappa ^{ + + }}$-closed with the greatest lower bounds).
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2019
References
REFERENCES
- 6
- Cited by

