Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T17:45:52.601Z Has data issue: false hasContentIssue false
  • English
  • Français

INDESTRUCTIBILITY WHEN THE FIRST TWO MEASURABLE CARDINALS ARE STRONGLY COMPACT

Part of: Set theory

Published online by Cambridge University Press:  23 November 2021

ARTHUR W. APTER
ARTHUR W. APTER*
Affiliation:
DEPARTMENT OF MATHEMATICS BARUCH COLLEGE OF CUNYNEW YORK, NY10010, USA and DEPARTMENT OF MATHEMATICS THE CUNY GRADUATE CENTER 365 FIFTH AVENUE NEW YORK, NY10016, USAE-mail:awapter@alum.mit.eduURL: http://faculty.baruch.cuny.edu/aapter
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove two theorems concerning indestructibility properties of the first two strongly compact cardinals when these cardinals are in addition the first two measurable cardinals. Starting from two supercompact cardinals 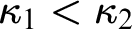$\kappa _1 < \kappa _2$ , we force and construct a model in which 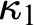$\kappa _1$ and 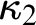$\kappa _2$ are both the first two strongly compact and first two measurable cardinals, 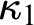$\kappa _1$ ’s strong compactness is fully indestructible (i.e., 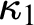$\kappa _1$ ’s strong compactness is indestructible under arbitrary 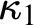$\kappa _1$ -directed closed forcing), and 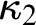$\kappa _2$ ’s strong compactness is indestructible under 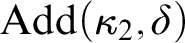$\mathrm {Add}(\kappa _2, \delta )$ for any ordinal 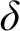$\delta $ . This provides an answer to a strengthened version of a question of Sargsyan found in [17, Question 5]. We also investigate indestructibility properties that may occur when the first two strongly compact cardinals are not only the first two measurable cardinals, but also exhibit nontrivial degrees of supercompactness.

Keywords

supercompact cardinalstrongly compact cardinalindestructibilitynonreflecting stationary set of ordinalslottery sumEaston support iteration of partial orderings

MSC classification

Primary: 03E35: Consistency and independence results
Secondary: 03E55: Large cardinals
Type
Article
Information
The Journal of Symbolic Logic , Volume 87 , Issue 1 , March 2022 , pp. 214 - 227
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Apter, A. and Cummings, J., Identity crises and strong compactness, this Journal, vol. 65 (2000), pp. 1895–1910.Google Scholar
Apter, A., Dimopoulos, S., and Usuba, T., Strongly compact cardinals and the continuum function . Annals of Pure and Applied Logic, vol. 172 (2021), no. 9, Article no $.$ 103013.CrossRefGoogle Scholar
Apter, A. and Gitik, M., The least measurable can be strongly compact and indestructible, this Journal, vol. 63 (1998), pp. 1404–1412.Google Scholar
Apter, A. and Hamkins, J. D., Exactly controlling the non-supercompact strongly compact cardinals, this Journal, vol. 68 (2003), pp. 669–688.Google Scholar
Apter, A. and Sargsyan, G., Universal indestructibility for degrees of supercompactness and strongly compact cardinals . Archive for Mathematical Logic, vol. 47 (2008), pp. 133–142.Google Scholar
Apter, A. and Shelah, S., On the strong equality between supercompactness and strong compactness . Transactions of the American Mathematical Society, vol. 349 (1997), pp. 103–128.CrossRefGoogle Scholar
Cummings, J., A model in which GCH holds at successors but fails at limits . Transactions of the American Mathematical Society, vol. 329 (1992), pp. 1–39.CrossRefGoogle Scholar
Foreman, M., More saturated ideals , Cabal Seminar 79–81, Lecture Notes in Mathematics, vol. 1019, Springer, Berlin–New York, 1983, pp. 1–27.CrossRefGoogle Scholar
Gitik, M., Changing cofinalities and the nonstationary ideal . Israel Journal of Mathematics, vol. 56 (1986), pp. 280–314.CrossRefGoogle Scholar
Hamkins, J. D., Gap forcing: generalizing the Lévy–Solovay theorem . The Bulletin of Symbolic Logic, vol. 5 (1999), pp. 264–272.CrossRefGoogle Scholar
Hamkins, J. D., The lottery preparation . Annals of Pure and Applied Logic, vol. 101 (2000), pp. 103–146.CrossRefGoogle Scholar
Hamkins, J. D., Gap forcing . Israel Journal of Mathematics, vol. 125 (2001), pp. 237–252.CrossRefGoogle Scholar
Jech, T., Set Theory, Springer, Berlin–New York, 2003.Google Scholar
Laver, R., Making the supercompactness of κ indestructible under κ-directed closed forcing . Israel Journal of Mathematics, vol. 29 (1978), pp. 385–388.CrossRefGoogle Scholar
Lévy, A. and Solovay, R., Measurable cardinals and the continuum hypothesis . Israel Journal of Mathematics, vol. 5 (1967), pp. 234–248.Google Scholar
Magidor, M., How large is the first strongly compact cardinal? Or a study on identity crises . Annals of Mathematical Logic, vol. 10 (1976), pp. 33–57.CrossRefGoogle Scholar
Sargsyan, G., On the indestructibility aspects of identity crisis . Archive for Mathematical Logic, vol. 48 (2009), pp. 493–513.CrossRefGoogle Scholar