No CrossRef data available.
Article contents
Infinitary properties of valued and ordered vector spaces
Published online by Cambridge University Press: 12 March 2014
Extract
§1. Introduction. The motivation of this work comes from two different directions: infinite abelian groups, and ordered algebraic structures. A challenging problem in both cases is that of classification. In the first case, it is known for example (cf. [KA]) that the classification of abelian torsion groups amounts to that of reduced p-groups by numerical invariants called the Ulm invariants (given by Ulm in [U]). Ulm's theorem was later generalized by P. Hill to the class of totally projective groups. As to the second case, let us consider for instance the class of divisible ordered abelian groups. These may be viewed as ordered ℚ-vector spaces. Their theory being unstable, we cannot hope to classify them by numerical invariants. On the other hand, being o-minimal, the theory enjoys several good model theoretic properties (cf. [P-S]), so the search for some reasonable invariants is well motivated. The common denominator of the two cases, as well as of many others, is valuation theory. Indeed given an ordered vector space, one can consider it as a valued vector space, endowed with the natural valuation. Also, the socle G[p] of a reduced abelian p-group G, endowed with the height function hG, is a valued vector space over 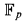 (the prime field of characteristic p) with values in the ordinals (cf. [F]).
(the prime field of characteristic p) with values in the ordinals (cf. [F]).
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1999

