Article contents
INITIAL SEGMENTS OF THE DEGREES OF CEERS
Published online by Cambridge University Press: 18 February 2022
Abstract
It is known that every non-universal self-full degree in the structure of the degrees of computably enumerable equivalence relations (ceers) under computable reducibility has exactly one strong minimal cover. This leaves little room for embedding wide partial orders as initial segments using self-full degrees. We show that considerably more can be done by staying entirely inside the collection of non-self-full degrees. We show that the poset 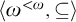 can be embedded as an initial segment of the degrees of ceers with infinitely many classes. A further refinement of the proof shows that one can also embed the free distributive lattice generated by the lower semilattice
can be embedded as an initial segment of the degrees of ceers with infinitely many classes. A further refinement of the proof shows that one can also embed the free distributive lattice generated by the lower semilattice 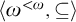 as an initial segment of the degrees of ceers with infinitely many classes.
as an initial segment of the degrees of ceers with infinitely many classes.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
- 1
- Cited by


