Article contents
INTERPRETABILITY LOGICS AND GENERALISED VELTMAN SEMANTICS
Published online by Cambridge University Press: 18 June 2020
Abstract
We obtain modal completeness of the interpretability logics IL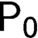 $\!\!\textsf {P}_{\textsf {0}}$ and ILR w.r.t. generalised Veltman semantics. Our proofs are based on the notion of full labels [2]. We also give shorter proofs of completeness w.r.t. the generalised semantics for many classical interpretability logics. We obtain decidability and finite model property w.r.t. the generalised semantics for IL
$\!\!\textsf {P}_{\textsf {0}}$ and ILR w.r.t. generalised Veltman semantics. Our proofs are based on the notion of full labels [2]. We also give shorter proofs of completeness w.r.t. the generalised semantics for many classical interpretability logics. We obtain decidability and finite model property w.r.t. the generalised semantics for IL $\textsf {P}_{\textsf {0}}$ and ILR. Finally, we develop a construction that might be useful for proofs of completeness of extensions of ILW w.r.t. the generalised semantics in the future, and demonstrate its usage with
$\textsf {P}_{\textsf {0}}$ and ILR. Finally, we develop a construction that might be useful for proofs of completeness of extensions of ILW w.r.t. the generalised semantics in the future, and demonstrate its usage with 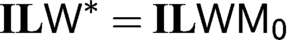 $\textbf {IL}\textsf {W}^\ast = \textbf {IL}\textsf {WM}_{\textsf {0}}$.
$\textbf {IL}\textsf {W}^\ast = \textbf {IL}\textsf {WM}_{\textsf {0}}$.
MSC classification
Information
- Type
- Articles
- Information
- Copyright
- © The Association for Symbolic Logic 2020
References
REFERENCES
- 7
- Cited by

