No CrossRef data available.
Article contents
INTERPRETATIONS BETWEEN ω-LOGIC AND SECOND-ORDER ARITHMETIC
Published online by Cambridge University Press: 18 August 2014
Abstract
This paper addresses the structures (M, ω) and (ω, SSy(M)), where M is a nonstandard model of PA and ω is the standard cut. It is known that (ω, SSy(M)) is interpretable in (M, ω). Our main technical result is that there is an reverse interpretation of (M, ω) in (ω, SSy(M)) which is ‘local’ in the sense of Visser [11]. We also relate the model theory of (M, ω) to the study of transplendent models of PA [2].
This yields a number of model theoretic results concerning the ω-models (M, ω) and their standard systems SSy(M, ω), including the following.
• 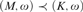 $\left( {M,\omega } \right) \prec \left( {K,\omega } \right)$ if and only if
$\left( {M,\omega } \right) \prec \left( {K,\omega } \right)$ if and only if 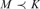 $M \prec K$ and
$M \prec K$ and 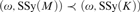 $\left( {\omega ,{\rm{SSy}}\left( M \right)} \right) \prec \left( {\omega ,{\rm{SSy}}\left( K \right)} \right)$.
$\left( {\omega ,{\rm{SSy}}\left( M \right)} \right) \prec \left( {\omega ,{\rm{SSy}}\left( K \right)} \right)$.
• 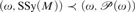 $\left( {\omega ,{\rm{SSy}}\left( M \right)} \right) \prec \left( {\omega ,{\cal P}\left( \omega \right)} \right)$ if and only if
$\left( {\omega ,{\rm{SSy}}\left( M \right)} \right) \prec \left( {\omega ,{\cal P}\left( \omega \right)} \right)$ if and only if 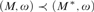 $\left( {M,\omega } \right) \prec \left( {{M^{\rm{*}}},\omega } \right)$ for some ω-saturated M*.
$\left( {M,\omega } \right) \prec \left( {{M^{\rm{*}}},\omega } \right)$ for some ω-saturated M*.
• 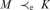 $M{ \prec _{\rm{e}}}K$ implies SSy(M, ω) = SSy(K, ω), but cofinal extensions do not necessarily preserve standard system in this sense.
$M{ \prec _{\rm{e}}}K$ implies SSy(M, ω) = SSy(K, ω), but cofinal extensions do not necessarily preserve standard system in this sense.
• SSy(M, ω)=SSy(M) if and only if (ω, SSy(M)) satisfies the full comprehension scheme.
• If SSy(M, ω) is uniformly defined by a single formula (analogous to a β function), then (ω, SSy(M, ω)) satisfies the full comprehension scheme; and there are models M for which SSy(M, ω) is not uniformly defined in this sense.
Keywords
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2014

