Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T18:49:20.935Z Has data issue: false hasContentIssue false
  • English
  • Français

INTERPRETING A FIELD IN ITS HEISENBERG GROUP

Part of: Connections with logic Model theory Other groups of matrices Computability and recursion theory

Published online by Cambridge University Press:  23 December 2021

RACHAEL ALVIR ,
WESLEY CALVERT ,
GRANT GOODMAN ,
VALENTINA HARIZANOV ,
JULIA KNIGHT ,
RUSSELL MILLER ,
ANDREY MOROZOV ,
ALEXANDRA SOSKOVA  and
ROSE WEISSHAAR
RACHAEL ALVIR
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF NOTRE DAME 255 HURLEY BLDG, NOTRE DAME, IN 46556, USA E-mail:rachael.c.alvir.1@nd.edu
WESLEY CALVERT
Affiliation:
SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES MAIL CODE 4408 SOUTHERN ILLINOIS UNIVERSITY CARBONDALE, IL 62918, USA E-mail:wcalvert@siu.edu
VALENTINA HARIZANOV
Affiliation:
DEPARTMENT OF MATHEMATICS GEORGE WASHINGTON UNIVERSITY WASHINGTON, DC 20052, USA E-mail:harizanv@gwu.edu
JULIA KNIGHT
Affiliation:
EMERITUS, DEPARTMENT OF MATHEMATICS UNIVERSITY OF NOTRE DAME 255 HURLEY BLDG, NOTRE DAME, IN 46556, USA E-mail:julia.f.knight.1@nd.edu
RUSSELL MILLER
Affiliation:
MATHEMATICS DEPT. QUEENS COLLEGE -- CUNY 65-30 KISSENA BLVD. QUEENS, NY 11367, USA and PHD PROGRAMS IN MATHEMATICS AND COMPUTER SCIENCE CUNY GRADUATE CENTER 365 FIFTH AVENUE NEW YORK, NY 10016, USA E-mail:russell.miller@qc.cuny.edu
ANDREY MOROZOV
Affiliation:
SOBOLEV INSTITUTE OF MATHEMATICS SB RAS KOPTYUG AVE. 4 NOVOSIBIRSK, 630090, RUSSIA E-mail:morozov@math.nsc.ru
ALEXANDRA SOSKOVA
Affiliation:
DEPT. OF MATHEMATICAL LOGIC FACULTY OF MATH AND COMP. SCI, SOFIA UNIVERSITY 5 JAMES BOURCHIER BLVD. 1164, SOFIA, BULGARIA E-mail:asoskova@fmi.uni-sofia.bg
ROSE WEISSHAAR
Affiliation:
DEPARTMENT OF MATHEMATICS AND STATISTICS WAKE FOREST UNIVERSITY WINSTON-SALEM, NC, 27101, USA E-mail:rweisshaar11@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We improve on and generalize a 1960 result of Maltsev. For a field F, we denote by 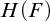$H(F)$ the Heisenberg group with entries in F. Maltsev showed that there is a copy of F defined in 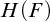$H(F)$ , using existential formulas with an arbitrary non-commuting pair of elements as parameters. We show that F is interpreted in 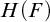$H(F)$ using computable 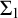$\Sigma _1$ formulas with no parameters. We give two proofs. The first is an existence proof, relying on a result of Harrison-Trainor, Melnikov, R. Miller, and Montalbán. This proof allows the possibility that the elements of F are represented by tuples in 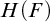$H(F)$ of no fixed arity. The second proof is direct, giving explicit finitary existential formulas that define the interpretation, with elements of F represented by triples in 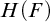$H(F)$ . Looking at what was used to arrive at this parameter-free interpretation of F in 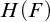$H(F)$ , we give general conditions sufficient to eliminate parameters from interpretations.

Keywords

Computabilitycomputable structure theoryHeisenberg group of a fieldinterpretationparameters

MSC classification

Primary: 03C57: Effective and recursion-theoretic model theory 03D45: Theory of numerations, effectively presented structures 20H20: Other matrix groups over fields 12L12: Model theory
Type
Article
Information
The Journal of Symbolic Logic , Volume 87 , Issue 3 , September 2022 , pp. 1215 - 1230
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Calvert, W., Cummins, D. F., Knight, J. F., and Miller, S., Comparing classes of finite structures . Algebra and Logic, vol. 43 (2004), pp. 374–392.CrossRefGoogle Scholar
Friedman, H. and Stanley, L., A Borel reducibility theory for classes of countable structures, this Journal, vol. 54 (1989), pp. 894–914.Google Scholar
Harrison-Trainor, M., Melnikov, A., Miller, R., and Montalbán, A., Computable functors and effective interpretability, this Journal, vol. 82 (2017), pp. 77–97.Google Scholar
Harrison-Trainor, M., Miller, R., and Montalbán, A., Borel functors and infinitary interpretations, this Journal, vol. 83 (2018), pp. 1434–1456.Google Scholar
Hirschfeldt, D. R., Khoussainov, B., Shore, R. A., and Slinko, A. M., Degree spectra and computable dimensions in algebraic structures . Annals of Pure and Applied Logic, vol. 115 (2002), pp. 71–113.CrossRefGoogle Scholar
Kalimullin, I., Algorithmic reducibilities of algebraic structures . Journal of Logic and Computation, vol. 22 (2012), pp. 831–843.CrossRefGoogle Scholar
Maltsev, A., Some correspondences between rings and groups . Matematicheskii Sbornik, New Series, vol. 50 (1960), pp. 257–266 (in Russian).Google Scholar
Mekler, A. H., Stability of nilpotent groups of class 2 and prime exponent, this Journal, vol. 46 (1981), pp. 781–788.Google Scholar
Miller, R., Poonen, B., Schoutens, H., and Shlapentokh, A., A computable functor from graphs to fields, this Journal, vol. 83 (2018), pp. 326–348.Google Scholar
Montalbán, A., Computable Structure Theory: Within the Arithmetic, Perspectives in Logic, Cambridge University Press, Cambridge, 2021.CrossRefGoogle Scholar
Scott, D., Logic with denumerably long formulas and finite strings of quantifiers , The Theory of Models (Addison, J. W., Henkin, L., and Tarski, A., editors), North-Holland, Amsterdam, 1965, pp. 329–341.Google Scholar