Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T19:24:24.906Z Has data issue: false hasContentIssue false
  • English
  • Français

ISOMORPHISM ON HYP

Published online by Cambridge University Press:  03 May 2016

SY-DAVID FRIEDMAN
SY-DAVID FRIEDMAN*
Affiliation:
KURT GÖDEL RESEARCH CENTER UNIVERSITY OF VIENNA WÄHRINGERSTRASSE 25 A-1090 VIENNA, AUSTRIAE-mail: sdf@logic.univie.ac.at
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that isomorphism is not a complete 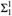${\rm{\Sigma }}_1^1$ equivalence relation even when restricted to the hyperarithmetic reals: If E1 denotes the 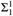${\rm{\Sigma }}_1^1$ (even 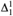${\rm{\Delta }}_1^1$) equivalence relation of [4] then for no Hyp function f do we have xEy iff f(x) is isomorphic to f(y) for all Hyp reals x,y. As a corollary to the proof we provide for each computable limit ordinal α a hyperarithmetic reduction of 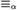${ \equiv _\alpha }$ (elementary-equivalence for sentences of quantifier-rank less than α) on arbitrary countable structures to isomorphism on countable structures of Scott rank at most α.

Keywords

Borel reducibilityhyperarithmeticisomorphism relations
Type
Articles
Information
The Journal of Symbolic Logic , Volume 81 , Issue 2 , June 2016 , pp. 395 - 399
Copyright
Copyright © The Association for Symbolic Logic 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Fokina, E., Friedman, S., Harizanov, V., Knight, J., McCoy, C., and Montalban, A., Isomorphism relations on computable structures , this Journal, vol. 77 (2012), no. 1, pp. 122–132.Google Scholar
Friedman, S., The completeness of isomorphism , Logic, Computation, Hierarchies, vol. 4, Series Ontos Mathematical Logic, de Gruyter, 2014.Google Scholar
Gao, S., Invariant descriptive set theory , Pure and Applied Mathematics, vol. 293, Taylor and Francis Group, 2009.Google Scholar
Kechris, A. and Louveau, A., The classification of hypersmooth Borel equivalence relations . Journal of the American Mathematical Society, vol. 10 (1997), no. 1, pp. 215–242.CrossRefGoogle Scholar