Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-13T09:53:27.898Z Has data issue: false hasContentIssue false
  • English
  • Français

The isomorphism property for nonstandard universes

Published online by Cambridge University Press:  12 March 2014

James H. Schmerl
James H. Schmerl*
Affiliation:
Department of Mathematics, University of Connecticut, Storrs, Connecticut 06268, E-mail: schmerl@uconnvm.uconn.edu
Get access Rights & Permissions [Opens in a new window]

Extract

The κ-isomorphism property (IPκ) for nonstandard universes was introduced by Henson in [4]. There has been some recent effort aimed at more fully understanding this property. Jin and Shelah in [7] have shown that for κ < ⊐ω, IPκ is equivalent to what we will refer to as the κ-resplendence property. Earlier, in [6], Jin asked if IPκ is equivalent to IPℵ0 plus κ-saturation. He answered this question positively for κ = ℵ1. In this note we extend this answer to all κ. We also extend the result of Jin and Shelah to all κ. (Jin also observed this could be done.)

In order to strike a balance between the generalities of model theory and the specifics of nonstandard analysis, we will consider models of Zermelo set theory with the Axiom of Choice; we denote this theory by ZC. The axioms of ZC are just those of ZFC but without the replacement scheme. Thus, among the axioms of ZC are the power set axiom, the infinity axiom, the separation axioms and the axiom of choice.

Let(V, E) ⊨ ZC. If a ∈ V, we let *a = {x ∈ V: (V,E) ⊨ x ∈ a}. In particular, i ∈ *ω iff i ∈ V and (V,E) ⊨ (i is a natural number). A subset A ⊆ V is internal if A = *a for some a ∈ V.

The standard model of ZC consists of those sets of rank at most ω + ω. In other words, if we let V0 be the set of hereditarily finite sets and 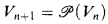for n < ω, then (Vω, ∈) is the standard model of ZC, where Vω = ⋃n<ω. Vn.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 60 , Issue 2 , June 1995 , pp. 512 - 516
Copyright
Copyright © Association for Symbolic Logic 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Barwise, J. and Schlipf, J., An introduction to recursively saturated and resplendent models, this Journal, vol. 41 (1976), pp. 531–536.Google Scholar
[2] Buechler, S., Expansions of models of co-stable theories, this Journal, vol. 49 (1984), pp. 470–477.Google Scholar
[3] Chang, C. C. and Keisler, H. J., Model theory, 3rd ed., North-Holland, Amsterdam, 1990.Google Scholar
[4] Henson, C. Ward, The isomorphism property in nonstandard analysis and its use in the theory of Banach spaces, this Journal, vol. 39 (1974), pp. 717–731.Google Scholar
[5] Jin, R., The isomorphism property versus the special model axiom, this Journal, vol. 57 (1992), pp. 975–987.Google Scholar
[6] Jin, R., A theorem on the isomorphism property, this Journal, vol. 57 (1992), pp. 1011–1017.Google Scholar
[7] Jin, R. and Shelah, S., The strength of the isomorphism property, this Journal, vol. 59 (1994), pp. 292–301.Google Scholar
[8] Keisler, H. J. and Schmerl, J. H., Making the hyperreal line both saturated and complete, this Journal, vol. 56 (1991), pp. 1016–1025.Google Scholar
[9] Schmerl, J. H., A reflection property and its application to nonstandard models, this Journal (to appear).Google Scholar