Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-13T09:07:47.008Z Has data issue: false hasContentIssue false
  • English
  • Français

Iterated reflection principles and the ω-rule

Published online by Cambridge University Press:  12 March 2014

Ulf R. Schmerl
Ulf R. Schmerl*
Affiliation:
Der Ludwio-Maximilians-Universitat, D-8000 Munchen 2, Federal, Republic of Germany
Get access Rights & Permissions [Opens in a new window]

Extract

The ω-rule,

with the meaning “if the formula A(n) is provable for all n, then the formula ∀xA(x) is provable”, has a certain formal similarity with a uniform reflection principle saying “if A(n) is provable for all n, then ∀xA(x) is true”. There are indeed some hints in the literature that uniform reflection has sometimes been understood as a “formalized ω-rule” (cf. for example S. Feferman [1], G. Kreisel [3], G. H. Müller [7]). This similarity has even another aspect: replacing the induction rule or scheme in Peano arithmetic PA by the ω-rule leads to a complete and sound system PA∞, where each true arithmetical statement is provable. In [2] Feferman showed that an equivalent system can be obtained by erecting on PA a transfinite progression of formal systems PAα based on iterations of the uniform reflection principle according to the following scheme:

Then T = (∪dЄ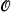, PAd, 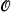being Kleene's system of ordinal notations, is equivalent to PA∞. Of course, T cannot be an axiomatizable theory.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 47 , Issue 4 , December 1982 , pp. 721 - 733
Copyright
Copyright © Association for Symbolic Logic 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Feferman, S., Systems of predicative analysis, this Journal, vol. 29 (1964), pp. 1–30.Google Scholar
[2]Feferman, S., Transfinite progressions of axiomatic theories, this Journal, vol. 27 (1962), pp. 259–316.Google Scholar
[3]Kreisel, G., Five notes on transfinite progressions, Technical Report No. 5, Applied Mathematics and Statistics Laboratory, Stanford University, California, 1962.Google Scholar
[4]Kreisel, G. and Lévy, A., Reflection principles and their use for establishing the complexity of axiomatic systems, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 14 (1968), pp. 97–142.CrossRefGoogle Scholar
[5]Lopez-Escobar, E. G. K., An extremely restricted ω-rule, Fundamenta Mathematicae, vol. 90 (1976), pp. 159–172.CrossRefGoogle Scholar
[6]Minc, G. E., Finite investigation of infinite derivations, Zapiski Naučnyh Seminarov Lenin-gradskogo Mathematičeskogo Instituto Akademii Nauk, vol. 49 (1975), pp. 67–122.Google Scholar
[7]Müller, G. H., Über die unendliche Induktion, Infinitistic methods, Pergamon, Oxford, 1961, pp. 75–95.Google Scholar
[8]Schmerl, U. R., Eine von Reflexionsformeln erzeugte Feinstruktur über Erweiterungen der primitiv rekursiven Arithmetik, Dissertation, Heidelberg, 1978.Google Scholar
[9]Schmerl, U. R., A fine structure generated by reflection formulas over primitive recursive arithmetic, Proceedings of the Logic Colloquium, Mons, 1978, North-Holland, Amsterdam, pp. 335–350.Google Scholar
[10]Schütte, K., Beweistheorie, Springer, Berlin, 1960.Google Scholar
[11]Schwichtenberg, H., Some applications of cut-elimination, Handbook of mathematical logic, North-Holland, Amsterdam, 1975, pp. 279–303.Google Scholar
[12]Sundholm, G., The omega-rule, a survey, Thesis, University of Oxford, 1978.Google Scholar