Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T18:40:37.075Z Has data issue: false hasContentIssue false
  • English
  • Français

Jump embeddings in the Turing degrees

Published online by Cambridge University Press:  12 March 2014

Peter G. Hinman  and
Theodore A. Slaman
Peter G. Hinman
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, Michigan 48109
Theodore A. Slaman
Affiliation:
Department of Mathematics, University of Chicago, Chicago, Illinois 60637
Get access Rights & Permissions [Opens in a new window]

Extract

Since its introduction in [K1-Po], the upper semilattice of Turing degrees has been an object of fascination to practitioners of the recursion-theoretic art. Starting from relatively simple concepts and definitions, it has turned out to be a structure of enormous complexity and richness. This paper is a contribution to the ongoing study of this structure.

Much of the work on Turing degrees may be formulated in terms of the embeddability of certain first-order structures in a structure whose universe is some set of degrees and whose relations, functions, and constants are natural degree-theoretic ones. Thus, for example, we know that if {P, ≤P) is a partial ordering of cardinality at most ℵ1 which is locally countable—each point has at most countably many predecessors—then there is an embedding

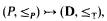
where D is the set of all Turing degrees and <T is Turing reducibility. If (P, ≤P) is a countable partial ordering, then the image of the embedding may be taken to be a subset of R, the set of recursively enumerable degrees. Without attempting to make the notion completely precise, we shall call embeddings of the first sort global, in contrast to local embeddings which impose some restrictions on the image set.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 56 , Issue 2 , June 1991 , pp. 563 - 591
Copyright
Copyright © Association for Symbolic Logic 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Ha]Harrison, J., Recursive pseudo-well-orderings, Transactions of the American Mathematical Society, vol. 131 (1968), pp. 526–543.CrossRefGoogle Scholar
[K1-Po]Kleene, S. C. and Post, E. L., The upper semi-lattice of degrees of recursive unsolvability, Annals of Mathematics, ser. 2, vol. 59 (1954), pp. 379–407. (Errata: Transactions of the American Mathematical Society, vol. 91 (1959), p. 52.)CrossRefGoogle Scholar
[Sh]Shore, R. A., Private communication.Google Scholar
[Si]Simpson, M. F., ω-REA operators and the range of the ω-jump on degrees below 0ω, manuscript derived from Ph.D. dissertation, Cornell University, Ithaca, New York, 1985.Google Scholar
[So]Soare, R. I., Recursively enumerable sets and degrees, Springer-Verlag, Berlin, 1987.CrossRefGoogle Scholar