Article contents
Lattice initial segments of the hyperdegrees
Published online by Cambridge University Press: 12 March 2014
Abstract
We affirm a conjecture of Sacks [1972] by showing that every countable distributive lattice is isomorphic to an initial segment of the hyperdegrees, 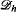 . In fact, we prove that every sublattice of any hyperarithmetic lattice (and so, in particular, every countable, locally finite lattice) is isomorphic to an initial segment of
. In fact, we prove that every sublattice of any hyperarithmetic lattice (and so, in particular, every countable, locally finite lattice) is isomorphic to an initial segment of 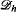 . Corollaries include the decidability of the two quantifier theory of
. Corollaries include the decidability of the two quantifier theory of 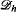 , and the undecidability of its three quantifier theory. The key tool in the proof is a new lattice representation theorem that provides a notion of forcing for which we can prove a version of the fusion lemma in the hyperarithmetic setting and so the preservation of ω1 ck . Somewhat surprisingly, the set theoretic analogof this forcing does not preserve ω1. On the other hand, we construct countable lattices that are not isomorphic to any initial segment of
, and the undecidability of its three quantifier theory. The key tool in the proof is a new lattice representation theorem that provides a notion of forcing for which we can prove a version of the fusion lemma in the hyperarithmetic setting and so the preservation of ω1 ck . Somewhat surprisingly, the set theoretic analogof this forcing does not preserve ω1. On the other hand, we construct countable lattices that are not isomorphic to any initial segment of 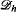 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2010
Footnotes
Partially supported by NSF Grants DMS-0554855 and DMS-0852811 and Grant 13408 from the John Templeton Foundation.
Partially supported by NSF grants DMS-0652669 and DMS-0901020. The authors also thank the referee for suggestions that improved the presentation in several ways.
References
REFERENCES
- 2
- Cited by

