Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T19:27:53.241Z Has data issue: false hasContentIssue false
  • English
  • Français

Le problème des grandes puissances et celui des grandes racines

Published online by Cambridge University Press:  12 March 2014

Natacha Portier
Natacha Portier*
Affiliation:
Laboratoire se l'Informatique du Paralleélisme, École Normal Supérieure de Lyon, 64 Alle'eed d'Italie, 69634 Lyon Cedex 07, France, E-mail:nportier@ens-lyon.fr
Get access Rights & Permissions [Opens in a new window]

Résumé

Soit f une fonction de N dans N qui ne soit pas calculable en temps polynomial, et a un élément d'un corps differentiel K de caractéristique nulle. Nous appelons probleme des grandes puissances l'ensembledes uples 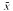= (x1…..xn) de K telsque x1 = af(n) et problème des grandes racines l'ensemble des uples 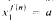de K tels que 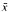. Ce sont deux exemples de problèmes que l'utilisation de la dérivée ne permet pas de résoudre plus rapidement. Nous montrons que le problème des grandes racines n'est pas polynomial au sens des corps differentiels, même si nous autorisons un nombre polynomial de paramètres. et que le problème des grandes puissances n'est pas polynomial au sens des corps differentiels. même au niveau non uniforme. Les démonstrations utilisent la stabilité polynomial de la théorie des corps de caractéristique nulle. montrée par L. Blum, F. dicker. M. Shub et S. Smale, ainsi que le lemme de réduction qui permet de ramener un polynôme differentiel des variables 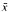a un polynôme des variables 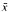et de leurs dérivées.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 65 , Issue 4 , December 2000 , pp. 1675 - 1685
Copyright
Copyright © Association for Symbolic Logic 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Blum, Lenore, Cucker, Felipe, Shub, Mike, and Smale, Steve, Algebraic settings for the problem “P ≠ NP?”, Mathematics of numerical analysis (Renegar, et al., editors), Lectures in Applied Mathematics, vol. 32, 1996, pp. 125–144.Google Scholar
[2]Everest, Graham, Measuring the height of a polynomial, The Mathematical Intelligencer, vol. 20 (1998), no. 3, pp. 9–16.CrossRefGoogle Scholar
[3]Lang, Serge, Fundamentals of diophantine geometry, Springer-Verlag, 1983.CrossRefGoogle Scholar
[4]Narkiewicz, Wladyslaw, Elementary and analytic theory of algebraic numbers, Springer-Verlag, PWN-Polish Scientific Publishers, 1990.Google Scholar
[5]Poizat, B., Les petits cailloux (Aleas, , editor), 1995.Google Scholar
[6]Portier, Natacha, Śtabilite polynÔmiale des corps diffÉrentiels, À paraitre dans this Journal.Google Scholar