LINEAR ORDERS REALIZED BY C.E. EQUIVALENCE RELATIONS

Abstract

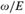Let E be a computably enumerable (c.e.) equivalence relation on the set ω of natural numbers. We say that the quotient set $\omega /E$ (or equivalently, the relation E) realizes a linearly ordered set 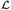${\cal L}$ if there exists a c.e. relation ⊴ respecting E such that the induced structure (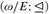$\omega /E$; ⊴) is isomorphic to 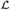${\cal L}$. Thus, one can consider the class of all linearly ordered sets that are realized by 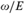$\omega /E$; formally, 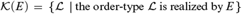${\cal K}\left( E \right) = \left\{ {{\cal L}\,|\,{\rm{the}}\,{\rm{order}}\, - \,{\rm{type}}\,{\cal L}\,{\rm{is}}\,{\rm{realized}}\,{\rm{by}}\,E} \right\}$. In this paper we study the relationship between computability-theoretic properties of E and algebraic properties of linearly ordered sets realized by E. One can also define the following pre-order 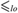$ \le _{lo} $ on the class of all c.e. equivalence relations: 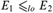$E_1 \le _{lo} E_2 $ if every linear order realized by E₁ is also realized by E₂. Following the tradition of computability theory, the lo-degrees are the classes of equivalence relations induced by the pre-order 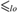$ \le _{lo} $. We study the partially ordered set of lo-degrees. For instance, we construct various chains and anti-chains and show the existence of a maximal element among the lo-degrees.