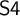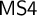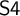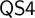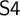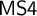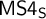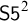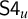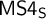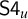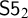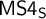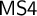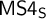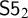1 Introduction
It is a classic result in modal logic, known as the Segerberg–Maksimova theorem, that a normal extension of
![]() $\mathsf {S4}$
is locally tabular iff it is of finite depth [Reference Maksimova25, Reference Segerberg30]. Since a logic is locally tabular iff its corresponding variety is locally finite, this provides a characterization of locally finite varieties of
$\mathsf {S4}$
is locally tabular iff it is of finite depth [Reference Maksimova25, Reference Segerberg30]. Since a logic is locally tabular iff its corresponding variety is locally finite, this provides a characterization of locally finite varieties of
![]() $\mathsf {S4}$
-algebras (see Section 4).
$\mathsf {S4}$
-algebras (see Section 4).
An important extension of
![]() $\mathsf {S4}$
is the bimodal logic
$\mathsf {S4}$
is the bimodal logic
![]() $\mathsf {MS4}$
—monadic
$\mathsf {MS4}$
—monadic
![]() $\mathsf {S4}$
—which axiomatizes the one-variable fragment of predicate
$\mathsf {S4}$
—which axiomatizes the one-variable fragment of predicate
![]() $\mathsf {S4}$
[Reference Fischer-Servi14]. It is known that a direct adaptation of the Segerberg–Maksimova theorem is no longer true for varieties of
$\mathsf {S4}$
[Reference Fischer-Servi14]. It is known that a direct adaptation of the Segerberg–Maksimova theorem is no longer true for varieties of
![]() $\mathsf {MS4}$
-algebras. Indeed, the well-known variety of two-dimensional diagonal-free cylindric algebras is not locally finite [Reference Henkin, Monk and Tarski18, Theorem 2.1.11], although it is precisely the variety of
$\mathsf {MS4}$
-algebras. Indeed, the well-known variety of two-dimensional diagonal-free cylindric algebras is not locally finite [Reference Henkin, Monk and Tarski18, Theorem 2.1.11], although it is precisely the variety of
![]() $\mathsf {MS4}$
-algebras of depth 1. This variety corresponds to the well-known bimodal system
$\mathsf {MS4}$
-algebras of depth 1. This variety corresponds to the well-known bimodal system
![]() $\mathsf {S5}^2$
, which axiomatizes the (diagonal-free) two-variable fragment of classical predicate logic (or, equivalently, the one-variable fragment of predicate
$\mathsf {S5}^2$
, which axiomatizes the (diagonal-free) two-variable fragment of classical predicate logic (or, equivalently, the one-variable fragment of predicate
![]() $\mathsf {S5}$
). Things improve when the attention is restricted to the bimodal logic
$\mathsf {S5}$
). Things improve when the attention is restricted to the bimodal logic
![]() $\mathsf {MGrz}$
—the one-variable fragment of predicate
$\mathsf {MGrz}$
—the one-variable fragment of predicate
![]() $\mathsf {Grz}$
(Grzegorczyk’s well-known modal logic [Reference Grzegorczyk17]). In this case, the Segerberg–Maksimova theorem has a direct generalization: a variety
$\mathsf {Grz}$
(Grzegorczyk’s well-known modal logic [Reference Grzegorczyk17]). In this case, the Segerberg–Maksimova theorem has a direct generalization: a variety
![]() $\mathbf {V}$
of
$\mathbf {V}$
of
![]() $\mathsf {MGrz}$
-algebras is locally finite iff it is of finite depth [Reference Bezhanishvili5, Section 4.10].
$\mathsf {MGrz}$
-algebras is locally finite iff it is of finite depth [Reference Bezhanishvili5, Section 4.10].
It is natural to seek a characterization of locally finite varieties of
![]() $\mathsf {MS4}$
-algebras. In the special case of
$\mathsf {MS4}$
-algebras. In the special case of
![]() $\mathsf {S5}^2$
-algebras, such a characterization was given in [Reference Bezhanishvili6, Section 4], where it was shown that every proper subvariety of the variety
$\mathsf {S5}^2$
-algebras, such a characterization was given in [Reference Bezhanishvili6, Section 4], where it was shown that every proper subvariety of the variety
![]() $\mathbf {S5}^2$
of all
$\mathbf {S5}^2$
of all
![]() $\mathsf {S5}^2$
-algebras is locally finite. As we pointed out above,
$\mathsf {S5}^2$
-algebras is locally finite. As we pointed out above,
![]() $\mathsf {S5}^2$
-algebras are exactly
$\mathsf {S5}^2$
-algebras are exactly
![]() $\mathsf {MS4}$
-algebras of depth 1. One of our main results (Section 6) shows that already a characterization of locally finite varieties of
$\mathsf {MS4}$
-algebras of depth 1. One of our main results (Section 6) shows that already a characterization of locally finite varieties of
![]() $\mathsf {S5}^2$
-algebras of depth 2 is at least as hard as characterizing locally finite varieties of
$\mathsf {S5}^2$
-algebras of depth 2 is at least as hard as characterizing locally finite varieties of
![]() $\mathbf {S5}_2$
—the variety corresponding to the fusion of
$\mathbf {S5}_2$
—the variety corresponding to the fusion of
![]() $\mathsf {S5}$
with itself. This problem, as well as the related problem of characterizing locally finite varieties of (unimodal)
$\mathsf {S5}$
with itself. This problem, as well as the related problem of characterizing locally finite varieties of (unimodal)
![]() $\mathsf {KTB}$
-algebras, remains wide open (see [Reference Shapirovsky31] for a recent treatment). This we do by demonstrating a translation of subvarieties of
$\mathsf {KTB}$
-algebras, remains wide open (see [Reference Shapirovsky31] for a recent treatment). This we do by demonstrating a translation of subvarieties of
![]() $\mathbf {S5}_2$
into subvarieties of
$\mathbf {S5}_2$
into subvarieties of
![]() $\mathbf {MS4}[2]$
—the variety of
$\mathbf {MS4}[2]$
—the variety of
![]() $\mathsf {MS4}$
-algebras of depth 2—that preserves and reflects local finiteness. Thus, already characterizing locally finite subvarieties of
$\mathsf {MS4}$
-algebras of depth 2—that preserves and reflects local finiteness. Thus, already characterizing locally finite subvarieties of
![]() $\mathbf {MS4}[2]$
would solve the problem of local finiteness for varieties of
$\mathbf {MS4}[2]$
would solve the problem of local finiteness for varieties of
![]() $\mathsf {S5}_2$
-algebras. In addition, we show that our translation does not naturally extend to depth 3 or higher, suggesting that in the general case local finiteness in
$\mathsf {S5}_2$
-algebras. In addition, we show that our translation does not naturally extend to depth 3 or higher, suggesting that in the general case local finiteness in
![]() $\mathbf {MS4}$
might be even more difficult. To summarize, characterizing locally finite varieties of
$\mathbf {MS4}$
might be even more difficult. To summarize, characterizing locally finite varieties of
![]() $\mathsf {MS4}$
-algebras is a hard problem.
$\mathsf {MS4}$
-algebras is a hard problem.
On the positive side, we show in Section 4 that the Segerberg–Maksimova theorem has an obvious generalization to a family of varieties containing
![]() $\mathbf {S4}_u$
which corresponds to the well-known bimodal logic
$\mathbf {S4}_u$
which corresponds to the well-known bimodal logic
![]() $\mathsf {S4}_u$
—
$\mathsf {S4}_u$
—
![]() $\mathsf {S4}$
with the universal modality—a logic that plays an important role in the study of the region-based theory of space (see, e.g., [Reference Aiello, Pratt-Hartmann and van Benthem1]). Both
$\mathsf {S4}$
with the universal modality—a logic that plays an important role in the study of the region-based theory of space (see, e.g., [Reference Aiello, Pratt-Hartmann and van Benthem1]). Both
![]() $\mathbf {S5}^2$
and
$\mathbf {S5}^2$
and
![]() $\mathbf {S4}_u$
are semisimple subvarieties of
$\mathbf {S4}_u$
are semisimple subvarieties of
![]() $\mathbf {MS4}$
. We identify in Section 3 the largest semisimple subvariety of
$\mathbf {MS4}$
. We identify in Section 3 the largest semisimple subvariety of
![]() $\mathbf {MS4}$
, which we denote by
$\mathbf {MS4}$
, which we denote by
![]() $\mathbf {MS4_S}$
. We prove that the corresponding bimodal logic
$\mathbf {MS4_S}$
. We prove that the corresponding bimodal logic
![]() $\mathsf {MS4_S}$
has the finite model property. Unfortunately, it is a hard problem to characterize local finiteness already in subvarieties of
$\mathsf {MS4_S}$
has the finite model property. Unfortunately, it is a hard problem to characterize local finiteness already in subvarieties of
![]() $\mathbf {MS4_S}$
as our translation lands in
$\mathbf {MS4_S}$
as our translation lands in
![]() $\mathbf {MS4_S}[2]$
.
$\mathbf {MS4_S}[2]$
.
These difficulties manifest themselves in the structure of dual spaces of finitely generated
![]() $\mathsf {MS4}$
-algebras. While the well-known coloring technique [Reference Esakia and Grigolia12] does generalize to
$\mathsf {MS4}$
-algebras. While the well-known coloring technique [Reference Esakia and Grigolia12] does generalize to
![]() $\mathsf {MS4}$
-algebras, unlike finitely generated
$\mathsf {MS4}$
-algebras, unlike finitely generated
![]() $\mathsf {S4}$
-algebras, the dual spaces of finitely generated
$\mathsf {S4}$
-algebras, the dual spaces of finitely generated
![]() $\mathsf {MS4}$
-algebras may have infinitely many points of finite depth. We demonstrate this by describing the dual space of the well-known Erdös–Tarski algebra, which is an infinite one-generated
$\mathsf {MS4}$
-algebras may have infinitely many points of finite depth. We demonstrate this by describing the dual space of the well-known Erdös–Tarski algebra, which is an infinite one-generated
![]() $\mathsf {S5}^2$
-algebra, thus has infinitely many points of depth 1. Some related open problems are posed in Section 5, and possible future directions of research are discussed in Section 7.
$\mathsf {S5}^2$
-algebra, thus has infinitely many points of depth 1. Some related open problems are posed in Section 5, and possible future directions of research are discussed in Section 7.
2 Preliminaries
Let
![]() $\mathcal L$
be a propositional modal language with two modalities
$\mathcal L$
be a propositional modal language with two modalities
![]() $\lozenge $
and
$\lozenge $
and
![]() $\exists $
. As usual, we write
$\exists $
. As usual, we write
![]() $\square = \neg \lozenge \neg $
and
$\square = \neg \lozenge \neg $
and
![]() $\forall = \neg \exists \neg $
.
$\forall = \neg \exists \neg $
.
Definition 2.1 [Reference Fischer-Servi14].
The bimodal logic
![]() $\mathsf {MS4}$
is the smallest normal modal logic in
$\mathsf {MS4}$
is the smallest normal modal logic in
![]() $\mathcal L$
containing
$\mathcal L$
containing
-
• The
 $\mathsf {S4}$
axioms for
$\mathsf {S4}$
axioms for
 $\lozenge $
(i.e., the
$\lozenge $
(i.e., the
 $\mathsf {K}$
axiom along with
$\mathsf {K}$
axiom along with
 $p \to \lozenge p$
and
$p \to \lozenge p$
and
 $\lozenge \lozenge p \to \lozenge p$
),
$\lozenge \lozenge p \to \lozenge p$
), -
• The
 $\mathsf {S5}$
axioms for
$\mathsf {S5}$
axioms for
 $\exists $
(e.g., the
$\exists $
(e.g., the
 $\mathsf {S4}$
axioms along with
$\mathsf {S4}$
axioms along with
 $\exists \forall p \to \forall p$
),
$\exists \forall p \to \forall p$
), -
• The left commutativity axiom
 $\exists \lozenge p \to \lozenge \exists p$
.
$\exists \lozenge p \to \lozenge \exists p$
.
Remark 2.2. In the terminology of [Reference Gabbay, Kurucz, Wolter and Zakharyaschev15],
![]() $\mathsf {MS4} = [\mathsf {S4}, \mathsf {S5}]^{\text {EX}}$
; that is,
$\mathsf {MS4} = [\mathsf {S4}, \mathsf {S5}]^{\text {EX}}$
; that is,
![]() $\mathsf {MS4}$
is the expanding relativized product of
$\mathsf {MS4}$
is the expanding relativized product of
![]() $\mathsf {S4}$
and
$\mathsf {S4}$
and
![]() $\mathsf {S5}$
.
$\mathsf {S5}$
.
Algebraic semantics for
![]() $\mathsf {MS4}$
is given by the following Boolean algebras with operators, first considered by Fischer–Servi [Reference Fischer-Servi14] under the name of bimodal algebras.
$\mathsf {MS4}$
is given by the following Boolean algebras with operators, first considered by Fischer–Servi [Reference Fischer-Servi14] under the name of bimodal algebras.
Definition 2.3. An
![]() $\mathsf {MS4}$
-algebra is a tuple
$\mathsf {MS4}$
-algebra is a tuple
![]() $\mathfrak {A} = (B, \lozenge , \exists )$
such that
$\mathfrak {A} = (B, \lozenge , \exists )$
such that
-
•
 $(B, \lozenge )$
is an
$(B, \lozenge )$
is an
 $\mathsf {S4}$
-algebra, i.e., B is a Boolean algebra and
$\mathsf {S4}$
-algebra, i.e., B is a Boolean algebra and
 $\lozenge $
is a unary function on B satisfying the identities of a closure operator:
$\lozenge $
is a unary function on B satisfying the identities of a closure operator:  $$\begin{align*}\lozenge 0 = 0 \qquad \lozenge (a \vee b) = \lozenge a \vee \lozenge b \qquad a \leq \lozenge a \qquad \lozenge \lozenge a \leq \lozenge a. \end{align*}$$
$$\begin{align*}\lozenge 0 = 0 \qquad \lozenge (a \vee b) = \lozenge a \vee \lozenge b \qquad a \leq \lozenge a \qquad \lozenge \lozenge a \leq \lozenge a. \end{align*}$$
-
•
 $(B, \exists )$
is an
$(B, \exists )$
is an
 $\mathsf {S5}$
-algebra, that is an
$\mathsf {S5}$
-algebra, that is an
 $\mathsf {S4}$
-algebra that in addition satisfies
$\mathsf {S4}$
-algebra that in addition satisfies
 $\exists \forall a \leq \forall a$
(where we write
$\exists \forall a \leq \forall a$
(where we write
 $-$
for Boolean negation and use standard abbreviations
$-$
for Boolean negation and use standard abbreviations
 $\square = {-} \lozenge {-}$
and
$\square = {-} \lozenge {-}$
and
 $\forall = {-} \exists {-}$
).
$\forall = {-} \exists {-}$
). -
•
 $\exists \lozenge a \leq \lozenge \exists a$
.
$\exists \lozenge a \leq \lozenge \exists a$
.
It is clear that the class of
![]() $\mathsf {MS4}$
-algebras is equationally definable, and hence forms a variety. We denote it and the corresponding category by
$\mathsf {MS4}$
-algebras is equationally definable, and hence forms a variety. We denote it and the corresponding category by
![]() $\mathbf {MS4}$
. The last axiom in the preceding definition has a few equivalent forms that we will make use of in the sequel.
$\mathbf {MS4}$
. The last axiom in the preceding definition has a few equivalent forms that we will make use of in the sequel.
Lemma 2.4. Each of the following identities is equivalent to the axiom
![]() $\exists \lozenge \leq \lozenge \exists $
:
$\exists \lozenge \leq \lozenge \exists $
:
-
(1)
 $\exists \lozenge \exists = \lozenge \exists $
(
$\exists \lozenge \exists = \lozenge \exists $
(
 $\exists $
preserves
$\exists $
preserves
 $\lozenge $
-fixpoints).
$\lozenge $
-fixpoints). -
(2)
 $\forall \square \forall = \square \forall $
(
$\forall \square \forall = \square \forall $
(
 $\forall $
preserves
$\forall $
preserves
 $\square $
-fixpoints).
$\square $
-fixpoints). -
(3)
 $\exists \square \leq \square \exists $
.
$\exists \square \leq \square \exists $
. -
(4)
 $\lozenge \forall \lozenge = \forall \lozenge $
(
$\lozenge \forall \lozenge = \forall \lozenge $
(
 $\lozenge $
preserves
$\lozenge $
preserves
 $\forall $
-fixpoints).
$\forall $
-fixpoints).
Proof. That the original axiom follows from (1) is obvious since
![]() $\exists $
is increasing. For the same reason, the axiom implies the
$\exists $
is increasing. For the same reason, the axiom implies the
![]() $(\geq )$
direction in (1), while the
$(\geq )$
direction in (1), while the
![]() $(\leq )$
direction follows since
$(\leq )$
direction follows since
![]() $\exists $
is idempotent. By taking Boolean negation, we see that (2) is equivalent to (1). That the axiom is equivalent to (3) is known, but not immediate; see [Reference Bezhanishvili and Carai3, Lemma 2.5]. Taking Boolean negation yields that (3) is equivalent to the inequality
$\exists $
is idempotent. By taking Boolean negation, we see that (2) is equivalent to (1). That the axiom is equivalent to (3) is known, but not immediate; see [Reference Bezhanishvili and Carai3, Lemma 2.5]. Taking Boolean negation yields that (3) is equivalent to the inequality
![]() $\lozenge \forall \leq \forall \lozenge $
, which in turn is equivalent to (4) in the same manner that (1) is equivalent to the original axiom.
$\lozenge \forall \leq \forall \lozenge $
, which in turn is equivalent to (4) in the same manner that (1) is equivalent to the original axiom.
Definition 2.5. For an
![]() $\mathsf {MS4}$
-algebra
$\mathsf {MS4}$
-algebra
![]() $\mathfrak {A} = (B, \lozenge , \exists )$
let
$\mathfrak {A} = (B, \lozenge , \exists )$
let
![]() $B_0$
be the set of
$B_0$
be the set of
![]() $\exists $
-fixpoints.
$\exists $
-fixpoints.
If
![]() $\lozenge _0$
is the restriction of
$\lozenge _0$
is the restriction of
![]() $\lozenge $
to
$\lozenge $
to
![]() $B_0$
, then it is straightforward to see that
$B_0$
, then it is straightforward to see that
![]() $(B_0, \lozenge _0)$
is an
$(B_0, \lozenge _0)$
is an
![]() $\mathsf {S4}$
-subalgebra of
$\mathsf {S4}$
-subalgebra of
![]() $(B, \lozenge )$
. We denote it by
$(B, \lozenge )$
. We denote it by
![]() $\mathfrak {A}_0$
.
$\mathfrak {A}_0$
.
Write
![]() $H_\square $
for the set of
$H_\square $
for the set of
![]() $\square $
-fixpoints of an
$\square $
-fixpoints of an
![]() $\mathsf {S4}$
-algebra
$\mathsf {S4}$
-algebra
![]() $(B, \lozenge )$
. It is well known (see, e.g., [Reference Esakia, Bezhanishvili and Holliday13, Proposition 2.2.4]) that
$(B, \lozenge )$
. It is well known (see, e.g., [Reference Esakia, Bezhanishvili and Holliday13, Proposition 2.2.4]) that
![]() $H_\square $
is a bounded sublattice of B which is a Heyting algebra, with Heyting implication given by
$H_\square $
is a bounded sublattice of B which is a Heyting algebra, with Heyting implication given by
![]() $a \to b = \square (-a \vee b)$
. The Heyting algebra
$a \to b = \square (-a \vee b)$
. The Heyting algebra
![]() $H_\square $
is sometimes called the skeleton of
$H_\square $
is sometimes called the skeleton of
![]() $(B, \lozenge )$
, and it is well known that, up to isomorphism, each Heyting algebra arises as the skeleton of some
$(B, \lozenge )$
, and it is well known that, up to isomorphism, each Heyting algebra arises as the skeleton of some
![]() $\mathsf {S4}$
-algebra (see, e.g., [Reference Esakia, Bezhanishvili and Holliday13, Section 2.5]). This plays a key role in proving faithfulness of the well-known Gödel translation of intuitionistic logic into
$\mathsf {S4}$
-algebra (see, e.g., [Reference Esakia, Bezhanishvili and Holliday13, Section 2.5]). This plays a key role in proving faithfulness of the well-known Gödel translation of intuitionistic logic into
![]() $\mathsf {S4}$
(see, e.g., [Reference Rasiowa and Sikorski29, Section XI.8]).
$\mathsf {S4}$
(see, e.g., [Reference Rasiowa and Sikorski29, Section XI.8]).
Remark 2.6. Similar to monadic Heyting algebras (see, e.g., [Reference Bezhanishvili8, Section 3]), we have that
![]() $\mathsf {MS4}$
-algebras can be represented as pairs of
$\mathsf {MS4}$
-algebras can be represented as pairs of
![]() $\mathsf {S4}$
-algebras
$\mathsf {S4}$
-algebras
![]() $(\mathfrak {A}, \mathfrak {A}_0)$
such that
$(\mathfrak {A}, \mathfrak {A}_0)$
such that
![]() $\mathfrak {A}_0$
is an
$\mathfrak {A}_0$
is an
![]() $\mathsf {S4}$
-subalgebra of
$\mathsf {S4}$
-subalgebra of
![]() $\mathfrak {A}$
and the inclusion
$\mathfrak {A}$
and the inclusion
![]() $\mathfrak {A}_0 \hookrightarrow \mathfrak {A}$
has a left adjoint
$\mathfrak {A}_0 \hookrightarrow \mathfrak {A}$
has a left adjoint
![]() $(\exists )$
.
$(\exists )$
.
We will make use of Jónsson–Tarski duality [Reference Jónsson and Tarski20] to work with the dual spaces of
![]() $\mathsf {MS4}$
-algebras. We recall some of the relevant notions:
$\mathsf {MS4}$
-algebras. We recall some of the relevant notions:
Definition 2.7. A topological space X is a Stone space if it is compact, Hausdorff, and zero-dimensional—that is, X has a basis of clopen sets (sets that are both closed and open).
Definition 2.8. Let X be a Stone space. We say that a relation
![]() $R \subseteq X^2$
is continuous if
$R \subseteq X^2$
is continuous if
-
(1)
 $R(x) := \left \{y \in X : x R y\right \}$
is closed for each
$R(x) := \left \{y \in X : x R y\right \}$
is closed for each
 $x \in X$
(R is point-closed).
$x \in X$
(R is point-closed). -
(2)
 $R^{-1}(U) := \left \{y \in X : yRx \text { for some } x \in U\right \}$
is clopen whenever
$R^{-1}(U) := \left \{y \in X : yRx \text { for some } x \in U\right \}$
is clopen whenever
 $U \subseteq X$
is clopen.
$U \subseteq X$
is clopen.
Specializing multimodal descriptive general frames (see, e.g., [Reference Blackburn, de Rijke and Venema9, Section 5.5]) to
![]() $\mathsf {MS4}$
yields.
$\mathsf {MS4}$
yields.
Definition 2.9. A descriptive
![]() $\mathsf {MS4}$
-frame is a tuple
$\mathsf {MS4}$
-frame is a tuple
![]() $\mathfrak {F} = (X, R, E)$
such that X is a Stone space, R is a quasi-order (reflexive and transitive), and E is an equivalence relation on X such that
$\mathfrak {F} = (X, R, E)$
such that X is a Stone space, R is a quasi-order (reflexive and transitive), and E is an equivalence relation on X such that
-
• both R and E are continuous relations,
-
•
 $RE {\kern-1.5pt}\subseteq{\kern-1.5pt} ER$
—that is,
$RE {\kern-1.5pt}\subseteq{\kern-1.5pt} ER$
—that is,
 $\forall x,y,y' {\kern-1.5pt}\in{\kern-1.5pt} X \; (x E y \text { and } y R y') {\kern-1.5pt}\to{\kern-1.5pt} \exists x' {\kern-1.5pt}\in{\kern-1.5pt} X{\kern-1.5pt} \; (x R x' {\kern-1pt}\text { and }{\kern-1pt} x' E y')$
.
$\forall x,y,y' {\kern-1.5pt}\in{\kern-1.5pt} X \; (x E y \text { and } y R y') {\kern-1.5pt}\to{\kern-1.5pt} \exists x' {\kern-1.5pt}\in{\kern-1.5pt} X{\kern-1.5pt} \; (x R x' {\kern-1pt}\text { and }{\kern-1pt} x' E y')$
.
We will refer to descriptive frames simply as frames because they are the only kind of frames we will deal with in this paper (as opposed to Kripke frames or the broader class of general frames studied in modal logic [Reference Blackburn, de Rijke and Venema9, Reference Chagrov and Zakharyaschev11]).
Remark 2.10. The subalgebra
![]() $\mathfrak {A}_0 = (B_0, \lozenge _0)$
of
$\mathfrak {A}_0 = (B_0, \lozenge _0)$
of
![]() $\exists $
-fixpoints (Definition 2.5) is dually identified with the
$\exists $
-fixpoints (Definition 2.5) is dually identified with the
![]() $\mathsf {S4}$
-frame
$\mathsf {S4}$
-frame
![]() $(X/E, \overline {R})$
of E-equivalence classes, where
$(X/E, \overline {R})$
of E-equivalence classes, where
The condition
![]() $RE \subseteq ER$
ensures that this is a well-defined quasi-order. In fact, this is a general construction arising from any correct partition of a descriptive frame [Reference Esakia and Grigolia12]. We discuss this in more detail in Section 5.
$RE \subseteq ER$
ensures that this is a well-defined quasi-order. In fact, this is a general construction arising from any correct partition of a descriptive frame [Reference Esakia and Grigolia12]. We discuss this in more detail in Section 5.
The next definition is well known (see, e.g., [Reference Blackburn, de Rijke and Venema9, Section 3.3]).
Definition 2.11. Let
![]() $X, X'$
be sets, S a binary relation on X, and
$X, X'$
be sets, S a binary relation on X, and
![]() $S'$
a binary relation on
$S'$
a binary relation on
![]() $X'$
. A function
$X'$
. A function
![]() $f : X \to X'$
is a p-morphism (or bounded morphism) with respect to
$f : X \to X'$
is a p-morphism (or bounded morphism) with respect to
![]() $(S, S')$
if
$(S, S')$
if
-
•
 $x S y$
implies
$x S y$
implies
 $f(x) S' f(y)$
;
$f(x) S' f(y)$
; -
•
 $f(x) S' y'$
implies
$f(x) S' y'$
implies
 $x S y$
for some
$x S y$
for some
 $y \in X$
with
$y \in X$
with
 $f(y) = y'$
.
$f(y) = y'$
.
Definition 2.12. An
![]() $\mathsf {MS4}$
-morphism is a continuous map
$\mathsf {MS4}$
-morphism is a continuous map
![]() $f:(X, R, E) \to (X', R', E')$
between
$f:(X, R, E) \to (X', R', E')$
between
![]() $\mathsf {MS4}$
-frames such that f is a p-morphism with respect to both
$\mathsf {MS4}$
-frames such that f is a p-morphism with respect to both
![]() $(R, R')$
and
$(R, R')$
and
![]() $(E, E')$
.
$(E, E')$
.
Specializing Jónsson–Tarski duality to
![]() $\mathsf {MS4}$
-algebras yields:
$\mathsf {MS4}$
-algebras yields:
Theorem 2.13. The category of
![]() $\mathsf {MS4}$
-algebras with homomorphisms and the category of descriptive
$\mathsf {MS4}$
-algebras with homomorphisms and the category of descriptive
![]() $\mathsf {MS4}$
-frames with
$\mathsf {MS4}$
-frames with
![]() $\mathsf {MS4}$
-morphisms are dually equivalent.
$\mathsf {MS4}$
-morphisms are dually equivalent.
Remark 2.14. The above dual equivalence is implemented as follows: with each
![]() $\mathsf {MS4}$
-frame
$\mathsf {MS4}$
-frame
![]() $\mathfrak {F} = (X, R, E)$
we associate the
$\mathfrak {F} = (X, R, E)$
we associate the
![]() $\mathsf {MS4}$
-algebra
$\mathsf {MS4}$
-algebra
![]() $\mathfrak {F}^* = (\operatorname {\mathrm {Clp}} X, \lozenge _R, \lozenge _E)$
of clopen subsets of X, where
$\mathfrak {F}^* = (\operatorname {\mathrm {Clp}} X, \lozenge _R, \lozenge _E)$
of clopen subsets of X, where
![]() $\lozenge _R$
and
$\lozenge _R$
and
![]() $\lozenge _E$
are the dual operators of R and E, defined by
$\lozenge _E$
are the dual operators of R and E, defined by
In the other direction, with each
![]() $\mathsf {MS4}$
-algebra
$\mathsf {MS4}$
-algebra
![]() $\mathfrak {A} = (B, \lozenge , \exists )$
we associate the descriptive frame
$\mathfrak {A} = (B, \lozenge , \exists )$
we associate the descriptive frame
![]() $\mathfrak {A}_* = (\operatorname {\mathrm {Uf}} B, R_\lozenge , R_\exists )$
of ultrafilters of B, where
$\mathfrak {A}_* = (\operatorname {\mathrm {Uf}} B, R_\lozenge , R_\exists )$
of ultrafilters of B, where
![]() $R_\lozenge $
and
$R_\lozenge $
and
![]() $R_\exists $
are the dual relations of
$R_\exists $
are the dual relations of
![]() $\lozenge $
and
$\lozenge $
and
![]() $\exists $
, defined by
$\exists $
, defined by
and
![]() $\operatorname {\mathrm {Uf}} B$
is equipped with the Stone topology generated by the clopen basis
$\operatorname {\mathrm {Uf}} B$
is equipped with the Stone topology generated by the clopen basis
![]() $\left \{\mathfrak {s}(a) : a \in B\right \}$
, where
$\left \{\mathfrak {s}(a) : a \in B\right \}$
, where
![]() $\mathfrak {s}(a) = \left \{x : a \in x\right \}$
. The unit isomorphisms of the duality are given by
$\mathfrak {s}(a) = \left \{x : a \in x\right \}$
. The unit isomorphisms of the duality are given by
-
•
 $\mathfrak {A} \to (\mathfrak {A}_*)^*$
;
$\mathfrak {A} \to (\mathfrak {A}_*)^*$
;
 $a \mapsto \left \{x : a \in x\right \}$
,
$a \mapsto \left \{x : a \in x\right \}$
, -
•
 $\mathfrak {F} \to (\mathfrak {F}^*)_*$
;
$\mathfrak {F} \to (\mathfrak {F}^*)_*$
;
 $x \mapsto \left \{a : x \in a\right \}$
.
$x \mapsto \left \{a : x \in a\right \}$
.
The dual of a morphism f (in both categories) is the inverse image map
![]() $f^{-1}[\cdot ]$
, and the natural bijection
$f^{-1}[\cdot ]$
, and the natural bijection
![]() $\operatorname {\mathrm {Hom}}(\mathfrak {A}, \mathfrak {F}^*) \cong \operatorname {\mathrm {Hom}}(\mathfrak {F}, \mathfrak {A}_*)$
is given by associating to
$\operatorname {\mathrm {Hom}}(\mathfrak {A}, \mathfrak {F}^*) \cong \operatorname {\mathrm {Hom}}(\mathfrak {F}, \mathfrak {A}_*)$
is given by associating to
![]() $f : \mathfrak {A} \to \mathfrak {F}^*$
the morphism
$f : \mathfrak {A} \to \mathfrak {F}^*$
the morphism
![]() $\bar {f} : \mathfrak {F} \to \mathfrak {A}_*$
defined by
$\bar {f} : \mathfrak {F} \to \mathfrak {A}_*$
defined by
![]() $x \mapsto \left \{a \in \mathfrak {A} : x \in f(a)\right \}$
, and to
$x \mapsto \left \{a \in \mathfrak {A} : x \in f(a)\right \}$
, and to
![]() $g : \mathfrak {F} \to \mathfrak {A}_*$
the morphism
$g : \mathfrak {F} \to \mathfrak {A}_*$
the morphism
![]() $\bar {g} : \mathfrak {A} \to \mathfrak {F}^*$
defined by
$\bar {g} : \mathfrak {A} \to \mathfrak {F}^*$
defined by
![]() $a \mapsto \left \{x \in \mathfrak {F} : a \in g(x)\right \}$
.
$a \mapsto \left \{x \in \mathfrak {F} : a \in g(x)\right \}$
.
3 Semisimple varieties
Recall [Reference Burris and Sankappanavar10, Section IV.12] that a variety
![]() $\mathbf {V}$
of algebras is semisimple if every subdirectly irreducible algebra from
$\mathbf {V}$
of algebras is semisimple if every subdirectly irreducible algebra from
![]() $\mathbf {V}$
is simple. It is well known that
$\mathbf {V}$
is simple. It is well known that
![]() $\mathbf {S5}$
is the largest semisimple subvariety of
$\mathbf {S5}$
is the largest semisimple subvariety of
![]() $\mathbf {S4}$
. In this section we introduce the largest semisimple subvariety of
$\mathbf {S4}$
. In this section we introduce the largest semisimple subvariety of
![]() $\mathbf {MS4}$
and its corresponding logic, which we denote by
$\mathbf {MS4}$
and its corresponding logic, which we denote by
![]() $\mathbf {MS4_S}$
and
$\mathbf {MS4_S}$
and
![]() $\mathsf {MS4_S}$
, respectively. The variety
$\mathsf {MS4_S}$
, respectively. The variety
![]() $\mathbf {MS4_S}$
contains two well-known varieties
$\mathbf {MS4_S}$
contains two well-known varieties
![]() $\mathbf {S5}^2$
and
$\mathbf {S5}^2$
and
![]() $\mathbf {S4}_u$
, whose corresponding logics are
$\mathbf {S4}_u$
, whose corresponding logics are
![]() $\mathsf {S5}^2$
[Reference Gabbay, Kurucz, Wolter and Zakharyaschev15, p. 230] and
$\mathsf {S5}^2$
[Reference Gabbay, Kurucz, Wolter and Zakharyaschev15, p. 230] and
![]() $\mathsf {S4}_u$
[Reference Gabbay, Kurucz, Wolter and Zakharyaschev15, p. 38]. One of our main results in this section shows that
$\mathsf {S4}_u$
[Reference Gabbay, Kurucz, Wolter and Zakharyaschev15, p. 38]. One of our main results in this section shows that
![]() $\mathbf {MS4_S}$
is generated by its finite algebras, and hence that
$\mathbf {MS4_S}$
is generated by its finite algebras, and hence that
![]() $\mathsf {MS4_S}$
has the finite model property (and is decidable).
$\mathsf {MS4_S}$
has the finite model property (and is decidable).
The standard correspondence between congruences and modal filters in BAOs (see [Reference Venema34, Section 4]) yields that the lattice of congruences of an
![]() $\mathbf {MS4}$
-algebra
$\mathbf {MS4}$
-algebra
![]() $\mathfrak {A}$
is isomorphic to the lattice of modal filters of
$\mathfrak {A}$
is isomorphic to the lattice of modal filters of
![]() $\mathfrak {A}$
, where a modal filter of
$\mathfrak {A}$
, where a modal filter of
![]() $\mathfrak {A}$
is a filter F satisfying
$\mathfrak {A}$
is a filter F satisfying
![]() $a \in F$
implies
$a \in F$
implies
![]() $\square a, \forall a \in F$
. Under standard duality theory (as outlined in Remark 2.14), filters of
$\square a, \forall a \in F$
. Under standard duality theory (as outlined in Remark 2.14), filters of
![]() $\mathfrak {A}$
closed under a modal necessity operator
$\mathfrak {A}$
closed under a modal necessity operator
![]() $\square $
correspond dually to closed subsets of
$\square $
correspond dually to closed subsets of
![]() $\mathfrak {A}_*$
that are
$\mathfrak {A}_*$
that are
![]() $R_\lozenge $
-upsets, i.e., closed subsets U such that
$R_\lozenge $
-upsets, i.e., closed subsets U such that
![]() $x \in U$
and
$x \in U$
and
![]() $x R_\lozenge y$
imply
$x R_\lozenge y$
imply
![]() $y \in U$
(where
$y \in U$
(where
![]() $R_\lozenge $
is the dual relation of
$R_\lozenge $
is the dual relation of
![]() $\lozenge $
). Hence, modal filters correspond dually to closed E-saturated R-upsets (we refer to E-upsets as E-saturated sets since they are unions of equivalence classes of E). We next give a nicer characterization of congruences of
$\lozenge $
). Hence, modal filters correspond dually to closed E-saturated R-upsets (we refer to E-upsets as E-saturated sets since they are unions of equivalence classes of E). We next give a nicer characterization of congruences of
![]() $\mathfrak {A}$
. For this we introduce an auxiliary
$\mathfrak {A}$
. For this we introduce an auxiliary
![]() $\mathsf {S4}$
-modality on
$\mathsf {S4}$
-modality on
![]() $\mathfrak {A}$
, and the corresponding auxiliary quasi-order on the dual descriptive frame of
$\mathfrak {A}$
, and the corresponding auxiliary quasi-order on the dual descriptive frame of
![]() $\mathfrak {A}$
.
$\mathfrak {A}$
.
Definition 3.1.
-
(1) For an
 $\mathsf {MS4}$
-algebra
$\mathsf {MS4}$
-algebra
 $\mathfrak A=(B, \lozenge , \exists )$
, define
$\mathfrak A=(B, \lozenge , \exists )$
, define
 $\blacklozenge = \lozenge \exists $
.
$\blacklozenge = \lozenge \exists $
. -
(2) For an
 $\mathsf {MS4}$
-frame
$\mathsf {MS4}$
-frame
 $\mathfrak F=(X, R, E)$
, define
$\mathfrak F=(X, R, E)$
, define
 $Q = ER$
.
$Q = ER$
.
Clearly
![]() $\blacklozenge $
is an
$\blacklozenge $
is an
![]() $\mathbf {S4}$
-possibility operator on B and Q is a quasi-order on X. The next lemma shows that Q is the dual relation of
$\mathbf {S4}$
-possibility operator on B and Q is a quasi-order on X. The next lemma shows that Q is the dual relation of
![]() $\blacklozenge $
. Let
$\blacklozenge $
. Let
![]() $\blacksquare = \neg \blacklozenge \neg $
. Then
$\blacksquare = \neg \blacklozenge \neg $
. Then
![]() $\blacksquare = \Box \forall $
and
$\blacksquare = \Box \forall $
and
![]() $\blacksquare $
is an
$\blacksquare $
is an
![]() $\mathsf {S4}$
-necessity operator on B. We let
$\mathsf {S4}$
-necessity operator on B. We let
![]() $H_\blacksquare $
be the Heyting algebra of fixpoints of
$H_\blacksquare $
be the Heyting algebra of fixpoints of
![]() $\blacksquare $
.
$\blacksquare $
.
Lemma 3.2. Let
![]() $\mathfrak A$
be an
$\mathfrak A$
be an
![]() $\mathsf {MS4}$
-algebra and
$\mathsf {MS4}$
-algebra and
![]() $\mathfrak F$
its dual
$\mathfrak F$
its dual
![]() $\mathsf {MS4}$
-frame. Then
$\mathsf {MS4}$
-frame. Then
![]() $xQy$
iff
$xQy$
iff
![]() $x\cap H_\blacksquare \subseteq y$
for each
$x\cap H_\blacksquare \subseteq y$
for each
![]() $x,y\in \mathfrak F$
.
$x,y\in \mathfrak F$
.
Proof. First suppose that
![]() $xQy$
and
$xQy$
and
![]() $a\in x\cap H_\blacksquare $
. Then there is z such that
$a\in x\cap H_\blacksquare $
. Then there is z such that
![]() $xRz$
and
$xRz$
and
![]() $zEy$
. Therefore,
$zEy$
. Therefore,
![]() $x\cap H_\square \subseteq z$
and
$x\cap H_\square \subseteq z$
and
![]() $z\cap B_0 =y\cap B_0$
. Since
$z\cap B_0 =y\cap B_0$
. Since
![]() $a\in H_\blacksquare $
, we have
$a\in H_\blacksquare $
, we have
![]() $a=\Box \forall a=\forall \Box \forall a$
(where the last equality follows from Lemma 2.4(2)), so
$a=\Box \forall a=\forall \Box \forall a$
(where the last equality follows from Lemma 2.4(2)), so
![]() $a\in H_\square \cap B_0$
. But then from
$a\in H_\square \cap B_0$
. But then from
![]() $a\in x$
it follows that
$a\in x$
it follows that
![]() $a\in z$
, which then implies that
$a\in z$
, which then implies that
![]() $a\in y$
. Thus,
$a\in y$
. Thus,
![]() $x\cap H_\blacksquare \subseteq y$
.
$x\cap H_\blacksquare \subseteq y$
.
Conversely, suppose that
![]() $x\cap H_\blacksquare \subseteq y$
. Let F be the filter generated by
$x\cap H_\blacksquare \subseteq y$
. Let F be the filter generated by
![]() $(x\cap H_\square )\cup (y\cap B_0)$
and I the ideal generated by
$(x\cap H_\square )\cup (y\cap B_0)$
and I the ideal generated by
![]() $B_0\setminus y$
. We show that
$B_0\setminus y$
. We show that
![]() $F \cap I = \varnothing $
. Otherwise there are
$F \cap I = \varnothing $
. Otherwise there are
![]() $a\in x\cap H_\square $
,
$a\in x\cap H_\square $
,
![]() $b\in y\cap B_0$
, and
$b\in y\cap B_0$
, and
![]() $c\in B_0\setminus y$
such that
$c\in B_0\setminus y$
such that
![]() $a\wedge b \le c$
. Therefore,
$a\wedge b \le c$
. Therefore,
![]() $a\le b\to c$
, so
$a\le b\to c$
, so
![]() $a \le \Box (b \to c)$
because
$a \le \Box (b \to c)$
because
![]() $a\in H_\square $
. Since
$a\in H_\square $
. Since
![]() $b,c\in B_0$
, we have
$b,c\in B_0$
, we have
![]() $\Box (b\to c)\in H_\blacksquare $
. Thus,
$\Box (b\to c)\in H_\blacksquare $
. Thus,
![]() $\Box (b\to c)\in x\cap H_\blacksquare \subseteq y$
, and so
$\Box (b\to c)\in x\cap H_\blacksquare \subseteq y$
, and so
![]() $b\to c\in y$
. Consequently,
$b\to c\in y$
. Consequently,
![]() $c \in y$
because
$c \in y$
because
![]() $b \in y$
. The obtained contradiction proves that
$b \in y$
. The obtained contradiction proves that
![]() $F\cap I=\varnothing $
. Therefore, there is an ultrafilter z such that
$F\cap I=\varnothing $
. Therefore, there is an ultrafilter z such that
![]() $x\cap H_\square \subseteq z$
and
$x\cap H_\square \subseteq z$
and
![]() $z\cap B_0=y\cap B_0$
. But then
$z\cap B_0=y\cap B_0$
. But then
![]() $xRz$
and
$xRz$
and
![]() $zEy$
, yielding that
$zEy$
, yielding that
![]() $xQy$
.
$xQy$
.
Definition 3.3. We call a filter F of an
![]() $\mathsf {MS4}$
-algebra a
$\mathsf {MS4}$
-algebra a
![]() $\blacksquare $
-filter if
$\blacksquare $
-filter if
![]() $a\in F$
implies
$a\in F$
implies
![]() $\blacksquare a \in F$
.
$\blacksquare a \in F$
.
We order the set of
![]() $\blacksquare $
-filters by inclusion. It is then clear that it is a complete lattice (because it is closed under arbitrary intersections). The next theorem generalizes the well-known correspondence (see, e.g., [Reference Esakia, Bezhanishvili and Holliday13, Sections 2.4 and 3.4]) between congruences and
$\blacksquare $
-filters by inclusion. It is then clear that it is a complete lattice (because it is closed under arbitrary intersections). The next theorem generalizes the well-known correspondence (see, e.g., [Reference Esakia, Bezhanishvili and Holliday13, Sections 2.4 and 3.4]) between congruences and
![]() $\square $
-filters of
$\square $
-filters of
![]() $\mathsf {S4}$
-algebras and closed upsets of their dual
$\mathsf {S4}$
-algebras and closed upsets of their dual
![]() $\mathsf {S4}$
-frames to the setting of
$\mathsf {S4}$
-frames to the setting of
![]() $\mathsf {MS4}$
-algebras.
$\mathsf {MS4}$
-algebras.
Theorem 3.4. Let
![]() $\mathfrak {A}$
be an
$\mathfrak {A}$
be an
![]() $\mathsf {MS4}$
-algebra and
$\mathsf {MS4}$
-algebra and
![]() $\mathfrak {F}$
its dual
$\mathfrak {F}$
its dual
![]() $\textsf {MS4}$
-frame. The following complete lattices are isomorphic:
$\textsf {MS4}$
-frame. The following complete lattices are isomorphic:
-
(1) Modal filters (and congruences) of
 $\mathfrak {A}$
.
$\mathfrak {A}$
. -
(2)
 $\blacksquare $
-filters of
$\blacksquare $
-filters of
 $\mathfrak {A}$
.
$\mathfrak {A}$
. -
(3) Modal filters (and congruences) of the
 $\mathsf {S4}$
-algebra
$\mathsf {S4}$
-algebra
 $\mathfrak {A}_0$
.
$\mathfrak {A}_0$
. -
(4) Filters (and congruences) of the Heyting algebra
 $H_\blacksquare $
.
$H_\blacksquare $
. -
(5) Closed Q-upsets of
 $\mathfrak {F}$
(under reverse inclusion).
$\mathfrak {F}$
(under reverse inclusion). -
(6) Closed E-saturated R-upsets of
 $\mathfrak {F}$
(under reverse inclusion).
$\mathfrak {F}$
(under reverse inclusion).
Proof. The modal filters and
![]() $\blacksquare $
-filters are literally the same lattice. Therefore, so are the closed Q-upsets and the closed E-saturated R-upsets of
$\blacksquare $
-filters are literally the same lattice. Therefore, so are the closed Q-upsets and the closed E-saturated R-upsets of
![]() $\mathfrak {F}$
. This gives the equivalence of (1), (2) and (5), (6). Note that the
$\mathfrak {F}$
. This gives the equivalence of (1), (2) and (5), (6). Note that the
![]() $\blacksquare $
-fixpoints of
$\blacksquare $
-fixpoints of
![]() $\mathfrak {A}$
are exactly the
$\mathfrak {A}$
are exactly the
![]() $\square $
-fixpoints of
$\square $
-fixpoints of
![]() $\mathfrak {A}_0$
, which yields the equivalence of (2) and (3), and also (4) by [Reference Esakia, Bezhanishvili and Holliday13, Theorem 2.4.17]. Finally, these are equivalent to (5) by [Reference Esakia, Bezhanishvili and Holliday13, Theorem 3.4.16].
$\mathfrak {A}_0$
, which yields the equivalence of (2) and (3), and also (4) by [Reference Esakia, Bezhanishvili and Holliday13, Theorem 2.4.17]. Finally, these are equivalent to (5) by [Reference Esakia, Bezhanishvili and Holliday13, Theorem 3.4.16].
Let
![]() $\mathfrak {F} = (X, R, E)$
be an
$\mathfrak {F} = (X, R, E)$
be an
![]() $\textsf {MS4}$
-frame. We call
$\textsf {MS4}$
-frame. We call
![]() $x \in X$
a Q-root of
$x \in X$
a Q-root of
![]() $\mathfrak {F}$
if
$\mathfrak {F}$
if
![]() $Q(x) = X$
. Then
$Q(x) = X$
. Then
![]() $\mathfrak {F}$
is Q-rooted if it has a Q-root, and strongly Q-rooted if the set of Q-roots is nonempty and open. A Q-cluster is an equivalence class of
$\mathfrak {F}$
is Q-rooted if it has a Q-root, and strongly Q-rooted if the set of Q-roots is nonempty and open. A Q-cluster is an equivalence class of
![]() $Q \cap Q^{-1}$
. The previous theorem then yields a characterization of simple and subdirectly irreducible algebras (we abbreviate subdirectly irreducible by s.i.):
$Q \cap Q^{-1}$
. The previous theorem then yields a characterization of simple and subdirectly irreducible algebras (we abbreviate subdirectly irreducible by s.i.):
Theorem 3.5. Let
![]() $\mathfrak {A}$
be a (non-trivial)
$\mathfrak {A}$
be a (non-trivial)
![]() $\mathsf {MS4}$
-algebra and
$\mathsf {MS4}$
-algebra and
![]() $\mathfrak {F}$
its dual
$\mathfrak {F}$
its dual
![]() $\textsf {MS4}$
-frame.
$\textsf {MS4}$
-frame.
-
(1)
 $\mathfrak {A}$
is s.i. iff
$\mathfrak {A}$
is s.i. iff
 $\mathfrak {F}$
is strongly Q-rooted.
$\mathfrak {F}$
is strongly Q-rooted. -
(2)
 $\mathfrak {A}$
is simple iff
$\mathfrak {A}$
is simple iff
 $\mathfrak {F}$
is a Q-cluster.
$\mathfrak {F}$
is a Q-cluster.
Proof. (1) It is well known (see, e.g., [Reference Burris and Sankappanavar10, Section II.8]) that
![]() $\mathfrak {A}$
is s.i. iff
$\mathfrak {A}$
is s.i. iff
![]() $\mathfrak {A}$
has a least nontrivial congruence. By the above theorem, this is equivalent to
$\mathfrak {A}$
has a least nontrivial congruence. By the above theorem, this is equivalent to
![]() $\mathfrak {F}$
having the largest closed Q-upset Y different from X. The complement of Y is the nonempty open set of Q-roots of
$\mathfrak {F}$
having the largest closed Q-upset Y different from X. The complement of Y is the nonempty open set of Q-roots of
![]() $\mathfrak {F}$
.
$\mathfrak {F}$
.
(2)
![]() $\mathfrak {A}$
is simple iff the only nontrivial congruence is
$\mathfrak {A}$
is simple iff the only nontrivial congruence is
![]() $A^2$
[Reference Burris and Sankappanavar10, Section II.8]. Thus, using (1),
$A^2$
[Reference Burris and Sankappanavar10, Section II.8]. Thus, using (1),
![]() $\mathfrak {A}$
is simple iff
$\mathfrak {A}$
is simple iff
![]() $Y=\varnothing $
, which is equivalent to
$Y=\varnothing $
, which is equivalent to
![]() $\mathfrak {F}$
being a Q-cluster.
$\mathfrak {F}$
being a Q-cluster.
Remark 3.6. The above theorem also follows from a general result of Venema [Reference Venema33]. For this it is enough to observe that Q is the reachability relation in an
![]() $\mathsf {MS4}$
-frame, and thus the above theorem follows from [Reference Venema33, Corollary 1].
$\mathsf {MS4}$
-frame, and thus the above theorem follows from [Reference Venema33, Corollary 1].
Let
![]() $\mathfrak {A}$
be a s.i.
$\mathfrak {A}$
be a s.i.
![]() $\mathsf {MS4}$
-algebra. By the above theorem,
$\mathsf {MS4}$
-algebra. By the above theorem,
![]() $\mathfrak {A}$
is simple iff
$\mathfrak {A}$
is simple iff
![]() $\blacklozenge $
is an
$\blacklozenge $
is an
![]() $\mathsf {S5}$
-possibility operator, which happens iff
$\mathsf {S5}$
-possibility operator, which happens iff
![]() $\blacklozenge \blacksquare a \le \blacksquare a$
for each
$\blacklozenge \blacksquare a \le \blacksquare a$
for each
![]() $a\in \mathfrak {A}$
. This motivates the following definition.
$a\in \mathfrak {A}$
. This motivates the following definition.
Definition 3.7. Define
![]() $\mathsf{MS4_S} = \mathsf{MS4} + \blacklozenge \blacksquare p \to \blacksquare p$
and its corresponding variety
$\mathsf{MS4_S} = \mathsf{MS4} + \blacklozenge \blacksquare p \to \blacksquare p$
and its corresponding variety
![]() $\mathbf{MS4_S} = \mathbf{MS4} + (\blacklozenge \blacksquare a \leq \blacksquare a)$
.
$\mathbf{MS4_S} = \mathbf{MS4} + (\blacklozenge \blacksquare a \leq \blacksquare a)$
.
Theorem 3.8.
![]() $\mathbf {MS4_S}$
is the largest semisimple subvariety of
$\mathbf {MS4_S}$
is the largest semisimple subvariety of
![]() $\mathbf {MS4}$
.
$\mathbf {MS4}$
.
Proof. Let
![]() $\mathbf {V}$
be a semisimple subvariety of
$\mathbf {V}$
be a semisimple subvariety of
![]() $\mathbf {MS4}$
and let
$\mathbf {MS4}$
and let
![]() $\mathfrak {A} \in \mathbf {V}$
be s.i. Then
$\mathfrak {A} \in \mathbf {V}$
be s.i. Then
![]() $\mathfrak {A}$
is simple, so the dual
$\mathfrak {A}$
is simple, so the dual
![]() $\textsf {MS4}$
-frame
$\textsf {MS4}$
-frame
![]() $\mathfrak {F}$
of
$\mathfrak {F}$
of
![]() $\mathfrak {A}$
is a Q-cluster by Theorem 3.5(2). Therefore, Q is an equivalence relation on
$\mathfrak {A}$
is a Q-cluster by Theorem 3.5(2). Therefore, Q is an equivalence relation on
![]() $\mathfrak {F}$
, and hence
$\mathfrak {F}$
, and hence
![]() $\mathfrak {A}\models \blacklozenge \blacksquare p \to \blacksquare p$
. Thus,
$\mathfrak {A}\models \blacklozenge \blacksquare p \to \blacksquare p$
. Thus,
![]() $\mathfrak {A}\in \mathbf {MS4_S}$
, and so
$\mathfrak {A}\in \mathbf {MS4_S}$
, and so
![]() $\mathbf {V}\subseteq \mathbf {MS4_S}$
.
$\mathbf {V}\subseteq \mathbf {MS4_S}$
.
Remark 3.9. The above theorem also follows from a general result of Kowalski and Kracht [Reference Kowalski and Kracht21, Theorem 12 and Proposition 8] that semisimplicity of a variety of modal algebras in finite signature is equivalent to the definability of a universal modality.
The two logics
![]() $\mathsf {S4}_u$
and
$\mathsf {S4}_u$
and
![]() $\mathsf {S5}^2$
mentioned in the introduction are actually both extensions of
$\mathsf {S5}^2$
mentioned in the introduction are actually both extensions of
![]() $\mathsf {MS4_S}$
. We recall the definitions.
$\mathsf {MS4_S}$
. We recall the definitions.
Definition 3.10.
-
(1) [Reference Bennett4, Reference Goranko and Passy16]
 $\mathsf {S4}_u$
is the smallest normal modal logic in
$\mathsf {S4}_u$
is the smallest normal modal logic in
 $\mathcal L$
containing the
$\mathcal L$
containing the
 $\mathsf {S4}$
axioms for
$\mathsf {S4}$
axioms for
 $\lozenge $
, the
$\lozenge $
, the
 $\mathsf {S5}$
axioms for
$\mathsf {S5}$
axioms for
 $\exists $
, and the bridge axiom
$\exists $
, and the bridge axiom
 $\lozenge p \to \exists p$
. Algebraically,
$\lozenge p \to \exists p$
. Algebraically,
 $\mathbf {S4}_u$
is the variety
$\mathbf {S4}_u$
is the variety
 $\mathbf {MS4} + (\lozenge a \leq \exists a)$
.
$\mathbf {MS4} + (\lozenge a \leq \exists a)$
. -
(2) [Reference Gabbay, Kurucz, Wolter and Zakharyaschev15, Section 5.1]
 $\mathsf {S5}^2$
is the product of
$\mathsf {S5}^2$
is the product of
 $\mathsf {S5}$
with itself, i.e. the smallest normal modal logic in
$\mathsf {S5}$
with itself, i.e. the smallest normal modal logic in
 $\mathcal L$
containing the
$\mathcal L$
containing the
 $\mathsf {S5}$
axioms for both
$\mathsf {S5}$
axioms for both
 $\lozenge ,\exists $
and the commutativity axiom
$\lozenge ,\exists $
and the commutativity axiom
 $\lozenge \exists p \leftrightarrow \exists \lozenge p$
. Algebraically,
$\lozenge \exists p \leftrightarrow \exists \lozenge p$
. Algebraically,
 $\mathbf {S5}^2$
is the variety
$\mathbf {S5}^2$
is the variety
 $\mathbf {MS4} + (\lozenge \square a \leq \square a)$
.
$\mathbf {MS4} + (\lozenge \square a \leq \square a)$
.
The variety
![]() $\mathbf {S5}^2$
is also known as the variety of diagonal-free cylindric algebras of dimension two [Reference Henkin, Monk and Tarski18, Definition 1.1.2]. Its subvarieties were studied in detail in [Reference Bezhanishvili6]. As we will see in Section 4,
$\mathbf {S5}^2$
is also known as the variety of diagonal-free cylindric algebras of dimension two [Reference Henkin, Monk and Tarski18, Definition 1.1.2]. Its subvarieties were studied in detail in [Reference Bezhanishvili6]. As we will see in Section 4,
![]() $\mathbf {S5}^2$
is the variety of all
$\mathbf {S5}^2$
is the variety of all
![]() $\mathsf {MS4}$
-algebras of depth 1.
$\mathsf {MS4}$
-algebras of depth 1.
Note that
![]() $\mathbf {S4}_u$
and
$\mathbf {S4}_u$
and
![]() $\mathbf {S5}^2$
are incomparable. Indeed, consider the frames
$\mathbf {S5}^2$
are incomparable. Indeed, consider the frames
![]() $\mathfrak {F}$
and
$\mathfrak {F}$
and
![]() $\mathfrak {G}$
depicted in Figure 1, where the black arrows represent R and dotted circles E. The dual algebra of
$\mathfrak {G}$
depicted in Figure 1, where the black arrows represent R and dotted circles E. The dual algebra of
![]() $\mathfrak {F}$
belongs to
$\mathfrak {F}$
belongs to
![]() $\mathbf {S4}_u$
since there is only one E-cluster, but evidently R is not an equivalence, so it does not belong to
$\mathbf {S4}_u$
since there is only one E-cluster, but evidently R is not an equivalence, so it does not belong to
![]() $\mathbf {S5}^2$
. On the other hand, the dual algebra of
$\mathbf {S5}^2$
. On the other hand, the dual algebra of
![]() $\mathfrak {G}$
belongs to
$\mathfrak {G}$
belongs to
![]() $\mathbf {S5}^2$
since R and E are commuting equivalence relations, but R-clusters are not contained in E-clusters, so the identity
$\mathbf {S5}^2$
since R and E are commuting equivalence relations, but R-clusters are not contained in E-clusters, so the identity
![]() $\lozenge a \leq \exists a$
of
$\lozenge a \leq \exists a$
of
![]() $\mathbf {S4}_u$
is falsified. Consequently, both
$\mathbf {S4}_u$
is falsified. Consequently, both
![]() $\mathbf {S4}_u$
and
$\mathbf {S4}_u$
and
![]() $\mathbf {S5}^2$
are proper subvarieties of
$\mathbf {S5}^2$
are proper subvarieties of
![]() $\mathbf {MS4_S}$
.
$\mathbf {MS4_S}$
.

Figure 1 The dual algebra of
![]() $\mathfrak {F}$
belongs to
$\mathfrak {F}$
belongs to
![]() $\mathbf {S4}_u$
but not to
$\mathbf {S4}_u$
but not to
![]() $\mathbf {S5}^2$
, and the opposite holds for the dual algebra of
$\mathbf {S5}^2$
, and the opposite holds for the dual algebra of
![]() $\mathfrak {G}$
.
$\mathfrak {G}$
.
While the characterization of locally finite subvarieties of these two varieties is known (see [Reference Bezhanishvili6] and Corollary 4.5 below), the question is dramatically more complicated for subvarieties of
![]() $\mathbf {MS4_S}$
, as will be demonstrated in Section 6.
$\mathbf {MS4_S}$
, as will be demonstrated in Section 6.
We conclude this section by establishing that
![]() $\mathbf {MS4_S}$
is generated by its finite members, and hence that
$\mathbf {MS4_S}$
is generated by its finite members, and hence that
![]() $\mathsf {MS4_S}$
has the finite model property (hereafter abbreviated fmp). For this we recall (see, e.g., [Reference Burris and Sankappanavar10, Definition II.10.14]) that an algebra is locally finite if every finitely generated subalgebra is finite.
$\mathsf {MS4_S}$
has the finite model property (hereafter abbreviated fmp). For this we recall (see, e.g., [Reference Burris and Sankappanavar10, Definition II.10.14]) that an algebra is locally finite if every finitely generated subalgebra is finite.
Lemma 3.11. If
![]() $\mathfrak {A} = (B, \lozenge , \exists )$
is an
$\mathfrak {A} = (B, \lozenge , \exists )$
is an
![]() $\mathsf {MS4_S}$
-algebra, then
$\mathsf {MS4_S}$
-algebra, then
![]() $(B, \blacklozenge , \exists )$
is a locally finite
$(B, \blacklozenge , \exists )$
is a locally finite
![]() $\mathsf {S5}^2$
-algebra.
$\mathsf {S5}^2$
-algebra.
Proof. Since
![]() $\mathfrak {A}$
is an
$\mathfrak {A}$
is an
![]() $\mathsf {MS4_S}$
-algebra,
$\mathsf {MS4_S}$
-algebra,
![]() $\blacklozenge $
is an
$\blacklozenge $
is an
![]() $\mathsf {S5}$
-operator. Moreover,
$\mathsf {S5}$
-operator. Moreover,
(the second equality follows from Lemma 2.4(1)). Therefore,
![]() $(B, \blacklozenge , \exists )$
is an
$(B, \blacklozenge , \exists )$
is an
![]() $\mathsf {S5}^2$
-algebra that in addition satisfies
$\mathsf {S5}^2$
-algebra that in addition satisfies
![]() $\exists \blacklozenge a = \blacklozenge a$
for each
$\exists \blacklozenge a = \blacklozenge a$
for each
![]() $a\in B$
. Thus,
$a\in B$
. Thus,
![]() $(B, \blacklozenge , \exists )$
belongs to a proper subvariety of
$(B, \blacklozenge , \exists )$
belongs to a proper subvariety of
![]() $\mathbf {S5}^2$
, which is locally finite by [Reference Bezhanishvili6, Section 4]. Consequently,
$\mathbf {S5}^2$
, which is locally finite by [Reference Bezhanishvili6, Section 4]. Consequently,
![]() $(B, \blacklozenge , \exists )$
is locally finite.
$(B, \blacklozenge , \exists )$
is locally finite.
Let
![]() $\mathfrak {A} = (B, \lozenge , \exists )$
be an
$\mathfrak {A} = (B, \lozenge , \exists )$
be an
![]() $\mathsf {MS4_S}$
-algebra. For a finite
$\mathsf {MS4_S}$
-algebra. For a finite
![]() $S \subseteq B$
, let
$S \subseteq B$
, let
![]() $B'$
be the subalgebra of
$B'$
be the subalgebra of
![]() $(B, \blacklozenge , \exists )$
generated by S. By the above lemma,
$(B, \blacklozenge , \exists )$
generated by S. By the above lemma,
![]() $B'$
is finite. Let K be the fixpoints of
$B'$
is finite. Let K be the fixpoints of
![]() $\lozenge $
, define
$\lozenge $
, define
![]() $\lozenge '$
on
$\lozenge '$
on
![]() $B'$
by
$B'$
by
and set
![]() $\mathfrak {A}_S=(B', \lozenge ', \exists )$
.
$\mathfrak {A}_S=(B', \lozenge ', \exists )$
.
Lemma 3.12.
![]() $\mathfrak {A}_S$
is a finite
$\mathfrak {A}_S$
is a finite
![]() $\mathsf {MS4_S}$
-algebra.
$\mathsf {MS4_S}$
-algebra.
Proof. As we already pointed out,
![]() $\mathfrak {A}_S$
is finite by Lemma 3.11. Moreover,
$\mathfrak {A}_S$
is finite by Lemma 3.11. Moreover,
![]() $\lozenge '$
is an
$\lozenge '$
is an
![]() $\mathbf {S4}$
-operator on
$\mathbf {S4}$
-operator on
![]() $\mathfrak {A}_S$
(see [Reference McKinsey and Tarski27, Lemma 2.3]). For the reader’s convenience, we sketch the proof of this result.
$\mathfrak {A}_S$
(see [Reference McKinsey and Tarski27, Lemma 2.3]). For the reader’s convenience, we sketch the proof of this result.
-
• That
 $\lozenge ' 0 = 0$
is clear since
$\lozenge ' 0 = 0$
is clear since
 $0 \in B' \cap K$
.
$0 \in B' \cap K$
. -
• That
 $\lozenge '(a \vee b) = \lozenge ' a \vee \lozenge ' b$
follows from distributivity since the meets involved in the definition of
$\lozenge '(a \vee b) = \lozenge ' a \vee \lozenge ' b$
follows from distributivity since the meets involved in the definition of
 $\lozenge '$
are finite.
$\lozenge '$
are finite. -
• That
 $a \leq \lozenge 'a$
follows from the definition of
$a \leq \lozenge 'a$
follows from the definition of
 $\lozenge ' a$
.
$\lozenge ' a$
. -
• To see that
 $\lozenge ' \lozenge ' a \leq \lozenge ' a$
, it is enough to observe that if
$\lozenge ' \lozenge ' a \leq \lozenge ' a$
, it is enough to observe that if
 $b\in B'\cap K$
, then
$b\in B'\cap K$
, then
 $a\le b$
iff
$a\le b$
iff
 $\Diamond ' a\le b$
.
$\Diamond ' a\le b$
.
We next show that
![]() $\exists \lozenge ' a \leq \lozenge ' \exists a$
, or equivalently that
$\exists \lozenge ' a \leq \lozenge ' \exists a$
, or equivalently that
![]() $\exists \lozenge ' \exists a = \lozenge ' \exists a$
, i.e. that
$\exists \lozenge ' \exists a = \lozenge ' \exists a$
, i.e. that
![]() $\lozenge ' \exists a$
is a
$\lozenge ' \exists a$
is a
![]() $\exists $
-fixpoint for each
$\exists $
-fixpoint for each
![]() $a\in \mathfrak {A}_S$
. First observe that if
$a\in \mathfrak {A}_S$
. First observe that if
![]() $b \in B' \cap K$
with
$b \in B' \cap K$
with
![]() $\exists a \leq b$
, then
$\exists a \leq b$
, then
![]() $\forall b \in B' \cap K$
(since
$\forall b \in B' \cap K$
(since
![]() $\lozenge \forall \lozenge = \forall \lozenge $
) and
$\lozenge \forall \lozenge = \forall \lozenge $
) and
![]() $\exists a \leq \forall b$
. Because
$\exists a \leq \forall b$
. Because
![]() $\forall b \leq b$
, we have
$\forall b \leq b$
, we have
![]() $\lozenge ' \exists a = \bigwedge \left \{\forall b : b \in B' \cap K, \exists a \leq b\right \}$
. But this is a finite meet of
$\lozenge ' \exists a = \bigwedge \left \{\forall b : b \in B' \cap K, \exists a \leq b\right \}$
. But this is a finite meet of
![]() $\exists $
-fixpoints and hence an
$\exists $
-fixpoints and hence an
![]() $\exists $
-fixpoint.
$\exists $
-fixpoint.
Finally, we check
![]() $\blacklozenge ' \blacksquare ' a \leq \blacksquare ' a$
for each
$\blacklozenge ' \blacksquare ' a \leq \blacksquare ' a$
for each
![]() $a\in B'$
, where
$a\in B'$
, where
![]() $\blacklozenge ' = \lozenge ' \exists $
and
$\blacklozenge ' = \lozenge ' \exists $
and
![]() $\blacksquare ' = {-} \blacklozenge ' {-}$
. Since
$\blacksquare ' = {-} \blacklozenge ' {-}$
. Since
![]() $\lozenge \exists a \in B'$
(because
$\lozenge \exists a \in B'$
(because
![]() $B'$
is closed under
$B'$
is closed under
![]() $\blacklozenge $
),
$\blacklozenge $
),
![]() $\lozenge ' \exists a = \lozenge \exists a$
, so
$\lozenge ' \exists a = \lozenge \exists a$
, so
![]() $\blacklozenge ' = \blacklozenge \vert _{B'}$
, and hence the inequality holds because
$\blacklozenge ' = \blacklozenge \vert _{B'}$
, and hence the inequality holds because
![]() $\mathfrak {A}$
is an
$\mathfrak {A}$
is an
![]() $\mathsf {MS4_S}$
-algebra.
$\mathsf {MS4_S}$
-algebra.
Theorem 3.13.
![]() $\mathsf {MS4_S}$
has the fmp.
$\mathsf {MS4_S}$
has the fmp.
Proof. If
![]() $\mathsf {MS4_S}\not \vdash \varphi $
, then there is an
$\mathsf {MS4_S}\not \vdash \varphi $
, then there is an
![]() $\mathsf {MS4_S}$
-algebra
$\mathsf {MS4_S}$
-algebra
![]() $\mathfrak {A} = (B, \lozenge , \exists )$
and an n-tuple
$\mathfrak {A} = (B, \lozenge , \exists )$
and an n-tuple
![]() $\overline {a}$
such that
$\overline {a}$
such that
![]() $\varphi (\overline {a}) \neq 1$
in
$\varphi (\overline {a}) \neq 1$
in
![]() $\mathfrak {A}$
. Let S be the set of subterms of
$\mathfrak {A}$
. Let S be the set of subterms of
![]() $\varphi (\overline {a})$
. Since S is finite,
$\varphi (\overline {a})$
. Since S is finite,
![]() $\mathfrak {A}_S = (B', \lozenge ', \exists )$
is a finite
$\mathfrak {A}_S = (B', \lozenge ', \exists )$
is a finite
![]() $\mathsf {MS4_S}$
-algebra by the previous lemma. Moreover, the definition of
$\mathsf {MS4_S}$
-algebra by the previous lemma. Moreover, the definition of
![]() $\lozenge '$
ensures that if
$\lozenge '$
ensures that if
![]() $\lozenge a \in B'$
, then
$\lozenge a \in B'$
, then
![]() $\lozenge ' a = \lozenge a$
. Therefore, the computation of
$\lozenge ' a = \lozenge a$
. Therefore, the computation of
![]() $\varphi (\overline {a})$
in
$\varphi (\overline {a})$
in
![]() $\mathfrak {A}_S$
is identical to that in
$\mathfrak {A}_S$
is identical to that in
![]() $\mathfrak {A}$
, and hence
$\mathfrak {A}$
, and hence
![]() $\varphi (\overline {a}) \neq 1$
in
$\varphi (\overline {a}) \neq 1$
in
![]() $\mathfrak {A}_S$
. Thus,
$\mathfrak {A}_S$
. Thus,
![]() $\varphi $
is falsified in
$\varphi $
is falsified in
![]() $\mathfrak {A}_S$
.
$\mathfrak {A}_S$
.
As a corollary we obtain the following pair of results, where the first concerns the finite-depth extensions of
![]() $\mathsf {MS4}$
(a notion we will define in Section 4).
$\mathsf {MS4}$
(a notion we will define in Section 4).
Corollary 3.14.
-
(1)
 $\mathsf {MS4_S} = \bigcap _n \mathsf {MS4_S}[n]$
.
$\mathsf {MS4_S} = \bigcap _n \mathsf {MS4_S}[n]$
. -
(2)
 $\mathsf {MS4_S}$
is decidable.
$\mathsf {MS4_S}$
is decidable.
Proof. (1) If
![]() $\mathsf {MS4_S} \not \vdash \varphi $
, then by the previous theorem,
$\mathsf {MS4_S} \not \vdash \varphi $
, then by the previous theorem,
![]() $\varphi $
is falsified on a finite
$\varphi $
is falsified on a finite
![]() $\mathsf {MS4_S}$
-algebra
$\mathsf {MS4_S}$
-algebra
![]() $\mathfrak {A}$
. Let n be the depth of
$\mathfrak {A}$
. Let n be the depth of
![]() $\mathfrak {A}$
. Then
$\mathfrak {A}$
. Then
![]() $\mathfrak {A}\models \mathsf {MS4_S}[n]$
, so
$\mathfrak {A}\models \mathsf {MS4_S}[n]$
, so
![]() $\mathsf {MS4_S}[n] \not \vdash \varphi $
, and hence
$\mathsf {MS4_S}[n] \not \vdash \varphi $
, and hence
![]() $\bigcap _n \mathsf {MS4_S}[n]\not \vdash \varphi $
.
$\bigcap _n \mathsf {MS4_S}[n]\not \vdash \varphi $
.
(2) This is obvious since
![]() $\mathsf {MS4_S}$
is finitely axiomatizable and has the fmp.
$\mathsf {MS4_S}$
is finitely axiomatizable and has the fmp.
4 Local finiteness
A classic result of Segerberg and Maksimova gives a characterization of local finiteness in the lattice of subvarieties of
![]() $\mathbf {S4}$
. By the depth of an
$\mathbf {S4}$
. By the depth of an
![]() $\mathsf {S4}$
-algebra
$\mathsf {S4}$
-algebra
![]() $\mathfrak {A}$
or its dual frame
$\mathfrak {A}$
or its dual frame
![]() $\mathfrak {F}$
, we mean the longest length of a proper R-chain in
$\mathfrak {F}$
, we mean the longest length of a proper R-chain in
![]() $\mathfrak {F}$
; that is, a sequence of points
$\mathfrak {F}$
; that is, a sequence of points
![]() $x_1 R x_2 R \dots R x_n$
where
$x_1 R x_2 R \dots R x_n$
where
![]() $\neg (x_j R x_i)$
for any
$\neg (x_j R x_i)$
for any
![]() $i < j$
. If there is no bound on such R-chains, then
$i < j$
. If there is no bound on such R-chains, then
![]() $\mathfrak {A}$
is of depth
$\mathfrak {A}$
is of depth
![]() $\omega $
. We say a variety
$\omega $
. We say a variety
![]() $\mathbf {V} \subseteq \mathbf {S4}$
has depth
$\mathbf {V} \subseteq \mathbf {S4}$
has depth
![]() $\leq n$
if the depth of each algebra in
$\leq n$
if the depth of each algebra in
![]() $\mathbf {V}$
is
$\mathbf {V}$
is
![]() $\leq n$
; if
$\leq n$
; if
![]() $\mathbf {V}$
contains algebras of arbitrary depth, we say it is of depth
$\mathbf {V}$
contains algebras of arbitrary depth, we say it is of depth
![]() $\omega $
. We will also apply these notions to (varieties of)
$\omega $
. We will also apply these notions to (varieties of)
![]() $\mathsf {MS4}$
-algebras and their dual frames, understanding the depth of an
$\mathsf {MS4}$
-algebras and their dual frames, understanding the depth of an
![]() $\mathsf {MS4}$
-algebra to be the depth of its
$\mathsf {MS4}$
-algebra to be the depth of its
![]() $\mathsf {S4}$
-reduct (that is, the R-depth of its dual frame).
$\mathsf {S4}$
-reduct (that is, the R-depth of its dual frame).
Consider the family of formulas
![]() $P_n$
defined by
$P_n$
defined by
It is well known (see, e.g., [Reference Chagrov and Zakharyaschev11, Theorem 3.44]) that a variety
![]() $\mathbf {V} \subseteq \mathbf {S4}$
has depth
$\mathbf {V} \subseteq \mathbf {S4}$
has depth
![]() $\leq n$
iff
$\leq n$
iff
![]() $\mathbf {V} \models P_n$
. Following [Reference Shapirovsky and Shehtman32], we write
$\mathbf {V} \models P_n$
. Following [Reference Shapirovsky and Shehtman32], we write
![]() $\mathbf {V}[n]$
to refer to the subvariety
$\mathbf {V}[n]$
to refer to the subvariety
![]() $\mathbf {V} + P_n$
. For example, since equivalence relations are precisely quasi-orders of depth 1, we have
$\mathbf {V} + P_n$
. For example, since equivalence relations are precisely quasi-orders of depth 1, we have
![]() $\mathbf {S4}[1] = \mathbf {S5}$
. Similarly,
$\mathbf {S4}[1] = \mathbf {S5}$
. Similarly,
![]() $\mathbf {S5}^2 = \mathbf {MS4}[1]$
. There is a pleasant analogy between
$\mathbf {S5}^2 = \mathbf {MS4}[1]$
. There is a pleasant analogy between
![]() $\mathbf {S5} \subseteq \mathbf {S4}$
and
$\mathbf {S5} \subseteq \mathbf {S4}$
and
![]() $\mathbf {MS4_S} \subseteq \mathbf {MS4}$
in that
$\mathbf {MS4_S} \subseteq \mathbf {MS4}$
in that
![]() $\mathbf {S5}$
is the largest subvariety of
$\mathbf {S5}$
is the largest subvariety of
![]() $\mathbf {S4}$
of R-depth 1, while
$\mathbf {S4}$
of R-depth 1, while
![]() $\mathbf {MS4_S}$
is the largest subvariety of
$\mathbf {MS4_S}$
is the largest subvariety of
![]() $\mathbf {MS4}$
of Q-depth 1. We have (see, e.g., [Reference Chagrov and Zakharyaschev11, Section 12.4]):
$\mathbf {MS4}$
of Q-depth 1. We have (see, e.g., [Reference Chagrov and Zakharyaschev11, Section 12.4]):
Theorem 4.1 (Segerberg–Maksimova).
A variety
![]() $\mathbf {V} \subseteq \mathbf {S4}$
is locally finite iff
$\mathbf {V} \subseteq \mathbf {S4}$
is locally finite iff
![]() $\mathbf {V} \models P_n$
for some
$\mathbf {V} \models P_n$
for some
![]() $n < \omega $
.
$n < \omega $
.
The lattice of subvarieties of
![]() $\mathbf {S4}$
has the structure depicted in Figure 2. In particular, the variety
$\mathbf {S4}$
has the structure depicted in Figure 2. In particular, the variety
![]() $\mathbf {Grz.3}$
, the subvariety of
$\mathbf {Grz.3}$
, the subvariety of
![]() $\mathbf {S4}$
defined by the formulas
$\mathbf {S4}$
defined by the formulas
is the least non-locally-finite subvariety of
![]() $\mathbf {S4}$
(and hence local finiteness below
$\mathbf {S4}$
(and hence local finiteness below
![]() $\mathbf {S4}$
is decidable). In the figure, the varieties
$\mathbf {S4}$
is decidable). In the figure, the varieties
![]() $\mathbf {Grz.3}[n]$
appearing on the right are the varieties generated by the single algebra whose dual space is the n-element chain, and
$\mathbf {Grz.3}[n]$
appearing on the right are the varieties generated by the single algebra whose dual space is the n-element chain, and
![]() $\mathbf {Grz.3}$
is the variety generated by all such algebras.
$\mathbf {Grz.3}$
is the variety generated by all such algebras.

Figure 2 The lattice of subvarieties of
![]() $\mathbf {S4}$
, dually isomorphic to the lattice of normal extensions of
$\mathbf {S4}$
, dually isomorphic to the lattice of normal extensions of
![]() $\mathsf {S4}$
. The locally finite varieties are precisely the ones below the dotted line.
$\mathsf {S4}$
. The locally finite varieties are precisely the ones below the dotted line.
It is natural to try to extend the Segerberg–Maksimova theorem to
![]() $\mathbf {MS4}$
. However, the theorem fails even in depth
$\mathbf {MS4}$
. However, the theorem fails even in depth
![]() $1$
since the variety
$1$
since the variety
![]() $\mathbf {MS4}[1] = \mathbf {S5}^2$
is not locally finite: the well-known Erdös–Tarski algebra is a one-generated infinite
$\mathbf {MS4}[1] = \mathbf {S5}^2$
is not locally finite: the well-known Erdös–Tarski algebra is a one-generated infinite
![]() $\mathbf {S5}^2$
-algebra (see, e.g., [Reference Henkin, Monk and Tarski18, Theorem 2.1.11]). Thus, finite depth does not characterize local finiteness in subvarieties of
$\mathbf {S5}^2$
-algebra (see, e.g., [Reference Henkin, Monk and Tarski18, Theorem 2.1.11]). Thus, finite depth does not characterize local finiteness in subvarieties of
![]() $\mathbf {MS4}$
. To the authors’ knowledge, the only positive result in this direction is that the Segerberg–Maksimova theorem holds for the variety
$\mathbf {MS4}$
. To the authors’ knowledge, the only positive result in this direction is that the Segerberg–Maksimova theorem holds for the variety
![]() $\mathbf {MGrz}$
of monadic Grzegorczyk algebras (see [Reference Bezhanishvili5, Section 4.10]).
$\mathbf {MGrz}$
of monadic Grzegorczyk algebras (see [Reference Bezhanishvili5, Section 4.10]).
In this paper we will make the case that characterizing local finiteness in subvarieties of
![]() $\mathbf {MS4}$
is a hard problem. In fact, we will show that a characterization of local finiteness even in subvarieties of
$\mathbf {MS4}$
is a hard problem. In fact, we will show that a characterization of local finiteness even in subvarieties of
![]() $\mathbf {MS4_S}[2]$
would yield one for
$\mathbf {MS4_S}[2]$
would yield one for
![]() $\mathbf {S5}_2$
. Here
$\mathbf {S5}_2$
. Here
![]() $\mathbf {S5}_2$
corresponds to the fusion
$\mathbf {S5}_2$
corresponds to the fusion
![]() $\mathsf {S5}_2 = \mathsf {S5} \oplus \mathsf {S5}$
, the bimodal logic of two
$\mathsf {S5}_2 = \mathsf {S5} \oplus \mathsf {S5}$
, the bimodal logic of two
![]() $\mathsf {S5}$
modalities with no connecting axioms (discussed in more detail in Section 6).
$\mathsf {S5}$
modalities with no connecting axioms (discussed in more detail in Section 6).
We do have the following criterion of local finiteness in subvarieties of
![]() $\mathbf {MS4}$
, but item (2) is in general hard to verify (as we will see shortly).
$\mathbf {MS4}$
, but item (2) is in general hard to verify (as we will see shortly).
Theorem 4.2. A subvariety
![]() $\mathbf {V}$
of
$\mathbf {V}$
of
![]() $\mathbf {MS4}$
is locally finite iff
$\mathbf {MS4}$
is locally finite iff
-
(1)
 $\mathbf {V}$
is of finite depth (
$\mathbf {V}$
is of finite depth (
 $\mathbf {V} \models P_k$
for some k);
$\mathbf {V} \models P_k$
for some k); -
(2) there is a function
 $f:\omega \to \omega $
such that for every n-generated s.i.
$f:\omega \to \omega $
such that for every n-generated s.i.
 $\mathfrak {A} \in \mathbf {V}$
, the algebra
$\mathfrak {A} \in \mathbf {V}$
, the algebra
 $\mathfrak {A}_0$
is
$\mathfrak {A}_0$
is
 $f(n)$
-generated as an
$f(n)$
-generated as an
 $\mathsf {S4}$
-algebra.
$\mathsf {S4}$
-algebra.
Proof. First suppose that
![]() $\mathbf {V}$
is locally finite. Then for every n, the free n-generated
$\mathbf {V}$
is locally finite. Then for every n, the free n-generated
![]() $\mathbf {V}$
-algebra is finite. Letting
$\mathbf {V}$
-algebra is finite. Letting
![]() $f(n)$
be its cardinality,
$f(n)$
be its cardinality,
![]() $f:\omega \to \omega $
is our desired function, and hence (2) is satisfied. Moreover, (1) is satisfied since the
$f:\omega \to \omega $
is our desired function, and hence (2) is satisfied. Moreover, (1) is satisfied since the
![]() $\mathbf {S4}$
-reduct of
$\mathbf {S4}$
-reduct of
![]() $\mathbf {V}$
is a uniformly locally finite class (that is, there is a uniform finite bound on the size of an n-generated subalgebra of an algebra from this class), and so it generates a locally finite variety (see [Reference Mal’cev, Smirnov and Taĭclin26, p. 285]). Thus,
$\mathbf {V}$
is a uniformly locally finite class (that is, there is a uniform finite bound on the size of an n-generated subalgebra of an algebra from this class), and so it generates a locally finite variety (see [Reference Mal’cev, Smirnov and Taĭclin26, p. 285]). Thus,
![]() $\mathbf {V}$
is of finite depth by the Segerberg–Maksimova theorem.
$\mathbf {V}$
is of finite depth by the Segerberg–Maksimova theorem.
Conversely, suppose that
![]() $\mathbf {V}$
satisfies (1) and (2). By [Reference Bezhanishvili5, Theorem 3.7(4)], it suffices to give a finite bound on the cardinality of every n-generated s.i.
$\mathbf {V}$
satisfies (1) and (2). By [Reference Bezhanishvili5, Theorem 3.7(4)], it suffices to give a finite bound on the cardinality of every n-generated s.i.
![]() $\mathfrak {A} \in \mathbf {V}$
. By (2),
$\mathfrak {A} \in \mathbf {V}$
. By (2),
![]() $\mathfrak {A}_0$
is an
$\mathfrak {A}_0$
is an
![]() $f(n)$
-generated
$f(n)$
-generated
![]() $\mathsf {S4}$
-algebra, and it is of finite depth because
$\mathsf {S4}$
-algebra, and it is of finite depth because
![]() $\mathfrak {A}$
is of finite depth by (1). Thus,
$\mathfrak {A}$
is of finite depth by (1). Thus,
![]() ${\lvert {B_0} \rvert } \leq k(n)$
by the Segerberg–Maksimova theorem. Since
${\lvert {B_0} \rvert } \leq k(n)$
by the Segerberg–Maksimova theorem. Since
![]() $B_0$
is the
$B_0$
is the
![]() $\exists $
-fixpoints of
$\exists $
-fixpoints of
![]() $\mathfrak {A}$
, we have that
$\mathfrak {A}$
, we have that
![]() $\mathfrak {A}$
is
$\mathfrak {A}$
is
![]() $(n + k(n))$
-generated as an
$(n + k(n))$
-generated as an
![]() $\mathsf {S4}$
-algebra, and thus we have some
$\mathsf {S4}$
-algebra, and thus we have some
![]() $m(n)$
such that
$m(n)$
such that
![]() ${\lvert {B} \rvert } \leq m(n + k(n))$
.
${\lvert {B} \rvert } \leq m(n + k(n))$
.
We next give a few applications of this theorem where (2) can be verified. For example, one can verify (2) by induction in the
![]() $\mathbf {MGrz}$
setting, as in [Reference Bezhanishvili5, Section. 4.10]. For another example, we need the following lemma.
$\mathbf {MGrz}$
setting, as in [Reference Bezhanishvili5, Section. 4.10]. For another example, we need the following lemma.
Lemma 4.3. Let
![]() $\mathfrak {A}$
be a s.i.
$\mathfrak {A}$
be a s.i.
![]() $\mathsf {MS4}$
-algebra. Then, for any
$\mathsf {MS4}$
-algebra. Then, for any
![]() $k \geq 1$
,
$k \geq 1$
,
![]() $\mathfrak {A}$
validates
$\mathfrak {A}$
validates
iff
![]() ${\lvert {\mathfrak{A}_0} \rvert } \leq 2^k$
.
${\lvert {\mathfrak{A}_0} \rvert } \leq 2^k$
.
Proof. The formula
![]() $\mathsf {alt}_k^0$
is obtained from the well-known formula
$\mathsf {alt}_k^0$
is obtained from the well-known formula
by substituting
![]() $\forall p_i$
for
$\forall p_i$
for
![]() $p_i$
. Let
$p_i$
. Let
![]() $\mathfrak {F} = (X, R, E)$
be the dual of
$\mathfrak {F} = (X, R, E)$
be the dual of
![]() $\mathfrak {A}$
. Since
$\mathfrak {A}$
. Since
![]() $\mathfrak {A}$
is s.i.,
$\mathfrak {A}$
is s.i.,
![]() $\mathfrak {F}$
is strongly Q-rooted by Theorem 3.5(1). Because the universe of the subalgebra
$\mathfrak {F}$
is strongly Q-rooted by Theorem 3.5(1). Because the universe of the subalgebra
![]() $\mathfrak {A}_0$
is exactly
$\mathfrak {A}_0$
is exactly
![]() $\forall $
-fixpoints of
$\forall $
-fixpoints of
![]() $\mathfrak {A}$
,
$\mathfrak {A}$
,
![]() $\mathfrak {A} \models \mathsf {alt}_k^0$
iff
$\mathfrak {A} \models \mathsf {alt}_k^0$
iff
![]() $\mathfrak {A}_0 \models \mathsf {alt}_k$
. By Remark 2.10, the dual space of
$\mathfrak {A}_0 \models \mathsf {alt}_k$
. By Remark 2.10, the dual space of
![]() $\mathfrak {A}_0$
is
$\mathfrak {A}_0$
is
![]() $\mathfrak {F}_0 = (X/E, \overline {R})$
, which is a rooted descriptive
$\mathfrak {F}_0 = (X/E, \overline {R})$
, which is a rooted descriptive
![]() $\mathsf {S4}$
-frame. Since
$\mathsf {S4}$
-frame. Since
![]() $\mathsf {alt}_k$
is a canonical formula ([Reference Blackburn, de Rijke and Venema9, Definition 4.30] together with [Reference Chagrov and Zakharyaschev11, Theorem 5.16]),
$\mathsf {alt}_k$
is a canonical formula ([Reference Blackburn, de Rijke and Venema9, Definition 4.30] together with [Reference Chagrov and Zakharyaschev11, Theorem 5.16]),
![]() $\mathsf {alt}_k$
is valid on
$\mathsf {alt}_k$
is valid on
![]() $\mathfrak {F}_0$
iff it is valid on the underlying Kripke frame of
$\mathfrak {F}_0$
iff it is valid on the underlying Kripke frame of
![]() $\mathfrak {F}_0$
([Reference Blackburn, de Rijke and Venema9, Proposition 5.85]). It is well known [Reference Chagrov and Zakharyaschev11, Proposition 3.45] that
$\mathfrak {F}_0$
([Reference Blackburn, de Rijke and Venema9, Proposition 5.85]). It is well known [Reference Chagrov and Zakharyaschev11, Proposition 3.45] that
![]() $\mathsf {alt}_k$
holds in a Kripke frame iff the number of alternatives of each point is
$\mathsf {alt}_k$
holds in a Kripke frame iff the number of alternatives of each point is
![]() $\leq k$
or, in the rooted transitive case, the number of points in the frame is
$\leq k$
or, in the rooted transitive case, the number of points in the frame is
![]() $\leq k$
. Thus,
$\leq k$
. Thus,
![]() $\mathsf {alt}_k^0$
holds on
$\mathsf {alt}_k^0$
holds on
![]() $\mathfrak {A}$
iff
$\mathfrak {A}$
iff
![]() ${\lvert {X/E} \rvert } \leq k$
or, equivalently,
${\lvert {X/E} \rvert } \leq k$
or, equivalently,
![]() ${\lvert {\mathfrak {A}_0} \rvert } \leq 2^k$
.
${\lvert {\mathfrak {A}_0} \rvert } \leq 2^k$
.
Theorem 4.4. For any
![]() $k \geq 1$
and
$k \geq 1$
and
![]() $\mathbf {V} \subseteq \mathbf {MS4} + (\mathsf {alt}_k^0 = 1)$
,
$\mathbf {V} \subseteq \mathbf {MS4} + (\mathsf {alt}_k^0 = 1)$
,
![]() $\mathbf {V}$
is locally finite iff it is of finite depth.
$\mathbf {V}$
is locally finite iff it is of finite depth.
Proof. We show that in this case Theorem 4.2(2) is always satisfied and the criterion reduces to being of finite depth. Let
![]() $\mathfrak {A} \in \mathbf {V}$
be s.i. and n-generated. By the above lemma,
$\mathfrak {A} \in \mathbf {V}$
be s.i. and n-generated. By the above lemma,
![]() ${\lvert {\mathfrak {A}_0} \rvert } \leq 2^k$
. Thus,
${\lvert {\mathfrak {A}_0} \rvert } \leq 2^k$
. Thus,
![]() $\mathfrak {A}_0$
is (at most)
$\mathfrak {A}_0$
is (at most)
![]() $2^k$
-generated.
$2^k$
-generated.
Since
![]() $\mathbf {S4}_u \models \mathsf {alt}_1^0$
(by Lemma 4.3), this also gives the following generalization of the Segerberg–Maksimova theorem to varieties of
$\mathbf {S4}_u \models \mathsf {alt}_1^0$
(by Lemma 4.3), this also gives the following generalization of the Segerberg–Maksimova theorem to varieties of
![]() $\mathsf {S4}_u$
-algebras:
$\mathsf {S4}_u$
-algebras:
Corollary 4.5.
![]() $\mathbf {V} \subseteq \mathbf {S4}_u$
is locally finite iff it is of finite depth.
$\mathbf {V} \subseteq \mathbf {S4}_u$
is locally finite iff it is of finite depth.
Remark 4.6. The formulas
![]() $E_i^k$
given in [Reference Bezhanishvili6, Theorem 4.2] bound the number of
$E_i^k$
given in [Reference Bezhanishvili6, Theorem 4.2] bound the number of
![]() $E_i$
-classes in a s.i.
$E_i$
-classes in a s.i.
![]() $\mathsf {S5}^2$
-algebra (note that
$\mathsf {S5}^2$
-algebra (note that
![]() $\mathbf {S5}^2$
is semisimple, so being s.i. amounts to being simple) by k or, equivalently, the size of the subalgebra of
$\mathbf {S5}^2$
is semisimple, so being s.i. amounts to being simple) by k or, equivalently, the size of the subalgebra of
![]() $\exists _i$
-fixpoints by
$\exists _i$
-fixpoints by
![]() $2^k$
. Therefore, the local finiteness of the subvarieties of
$2^k$
. Therefore, the local finiteness of the subvarieties of
![]() $\mathbf {S5}^2$
defined by the
$\mathbf {S5}^2$
defined by the
![]() $E_i^k$
as given in [Reference Bezhanishvili6, Lemma 4.4] also follows from our criterion.
$E_i^k$
as given in [Reference Bezhanishvili6, Lemma 4.4] also follows from our criterion.
In the general case, however, verifying Theorem 4.2(2) is more complex. In Section 6 we demonstrate that completely characterizing local finiteness even in
![]() $\mathbf {MS4_S}[2]$
would also do so for
$\mathbf {MS4_S}[2]$
would also do so for
![]() $\mathbf {S5}_2$
, which is an open problem as mentioned in the introduction. We do this by demonstrating a translation from subvarieties of
$\mathbf {S5}_2$
, which is an open problem as mentioned in the introduction. We do this by demonstrating a translation from subvarieties of
![]() $\mathbf {S5}_2$
to subvarieties of
$\mathbf {S5}_2$
to subvarieties of
![]() $\mathbf {MS4_S}[2]$
that preserves and reflects local finiteness. Before that, we will focus our discussion on the behavior of finitely generated
$\mathbf {MS4_S}[2]$
that preserves and reflects local finiteness. Before that, we will focus our discussion on the behavior of finitely generated
![]() $\mathsf {MS4}$
-algebras.
$\mathsf {MS4}$
-algebras.
5 Finitely generated algebras
In this section we obtain several results about finitely generated
![]() $\mathsf {MS4}$
-algebras, including the description of the dual space of the Erdös–Tarski algebra. We will see that they are significantly more complex than finitely generated
$\mathsf {MS4}$
-algebras, including the description of the dual space of the Erdös–Tarski algebra. We will see that they are significantly more complex than finitely generated
![]() $\mathsf {S4}$
-algebras. We conclude the section with several open problems about finitely generated
$\mathsf {S4}$
-algebras. We conclude the section with several open problems about finitely generated
![]() $\mathsf {MS4}$
-algebras.
$\mathsf {MS4}$
-algebras.
We start by recalling the notion of a (quasi-)maximal point (see [Reference Esakia, Bezhanishvili and Holliday13, Definition 1.4.9]).
Definition 5.1. Let X be a set and R a quasi-order on X. Given
![]() $A \subseteq X$
, we write
$A \subseteq X$
, we write
(so for us,
![]() $\max $
means “quasi-maximum”). We define the n-th layer of X inductively as
$\max $
means “quasi-maximum”). We define the n-th layer of X inductively as
 $$\begin{align*}D_1 = \max X \qquad D_{n+1} = \max \left( X - \bigcup_{i=1}^{n} D_i \right). \end{align*}$$
$$\begin{align*}D_1 = \max X \qquad D_{n+1} = \max \left( X - \bigcup_{i=1}^{n} D_i \right). \end{align*}$$
We may speak of the layers of an
![]() $\mathsf {S4}$
-frame or
$\mathsf {S4}$
-frame or
![]() $\mathsf {MS4}$
-frame, always referring to the R-layers. In the case of arbitrary quasi-orders, some or all
$\mathsf {MS4}$
-frame, always referring to the R-layers. In the case of arbitrary quasi-orders, some or all
![]() $D_i$
may be empty (e.g., when X contains infinite ascending chains). However, we have the following (see [Reference Esakia, Bezhanishvili and Holliday13, Corollary 3.2.2 and Theorem 3.2.3]).
$D_i$
may be empty (e.g., when X contains infinite ascending chains). However, we have the following (see [Reference Esakia, Bezhanishvili and Holliday13, Corollary 3.2.2 and Theorem 3.2.3]).
Theorem 5.2. Let
![]() $(X, R)$
be a descriptive
$(X, R)$
be a descriptive
![]() $\mathsf {S4}$
-frame. Then
$\mathsf {S4}$
-frame. Then
![]() $D_1 = \max X$
is nonempty and closed.
$D_1 = \max X$
is nonempty and closed.
Clearly this holds for descriptive
![]() $\mathsf {MS4}$
-frames as well. We concentrate on finitely generated descriptive frames; that is, frames
$\mathsf {MS4}$
-frames as well. We concentrate on finitely generated descriptive frames; that is, frames
![]() $\mathfrak {F}$
whose dual
$\mathfrak {F}$
whose dual
![]() $\mathfrak {F}^*$
is a finitely generated algebra. Finitely generated descriptive
$\mathfrak {F}^*$
is a finitely generated algebra. Finitely generated descriptive
![]() $\mathsf {S4}$
-frames have a relatively well-understood, but complicated structure. They consist of finite “discrete” layers, possibly with limit points of infinite depth.
$\mathsf {S4}$
-frames have a relatively well-understood, but complicated structure. They consist of finite “discrete” layers, possibly with limit points of infinite depth.
Theorem 5.3 (see, e.g., [Reference Chagrov and Zakharyaschev11, Section 8.6]).
Let
![]() $(X, R)$
be a finitely generated descriptive
$(X, R)$
be a finitely generated descriptive
![]() $\mathsf {S4}$
-frame. Then every
$\mathsf {S4}$
-frame. Then every
![]() $D_n$
(
$D_n$
(
![]() $n < \omega $
) is finite and consists of isolated points, hence is clopen.
$n < \omega $
) is finite and consists of isolated points, hence is clopen.
Remark 5.4. The same result also holds for Heyting algebras and their dual spaces; see [Reference Bezhanishvili7, Theorem 3.1.8].
This result does not carry over to the monadic setting. In fact, the Erdös–Tarski algebra is an infinite one-generated
![]() $\mathsf {S5}^2$
-algebra (see [Reference Henkin, Monk and Tarski18, Theorem 2.1.11]). Thus, its dual is an infinite one-generated descriptive
$\mathsf {S5}^2$
-algebra (see [Reference Henkin, Monk and Tarski18, Theorem 2.1.11]). Thus, its dual is an infinite one-generated descriptive
![]() $\mathsf {MS4}$
-frame of depth 1. It follows that finitely generated descriptive
$\mathsf {MS4}$
-frame of depth 1. It follows that finitely generated descriptive
![]() $\mathsf {MS4}$
-frames may have limit points already in depth 1. One of the main goals of this section is to describe the dual frame of the Erdös–Tarski algebra. For this purpose, we adjust the notion of a correct partition to the setting of
$\mathsf {MS4}$
-frames may have limit points already in depth 1. One of the main goals of this section is to describe the dual frame of the Erdös–Tarski algebra. For this purpose, we adjust the notion of a correct partition to the setting of
![]() $\mathsf {MS4}$
-frames.
$\mathsf {MS4}$
-frames.
Definition 5.5 [Reference Esakia and Grigolia12].
Let
![]() $\mathfrak {F} = (X, R, E)$
be an
$\mathfrak {F} = (X, R, E)$
be an
![]() $\mathsf {MS4}$
-frame. A correct partition of
$\mathsf {MS4}$
-frame. A correct partition of
![]() $\mathfrak {F}$
is an equivalence relation
$\mathfrak {F}$
is an equivalence relation
![]() $K \subseteq X^2$
such that
$K \subseteq X^2$
such that
-
(1) K is separated (or Boolean, as in [Reference Koppelberg, Monk and Bonnet22, Definition 8.3]), i.e., any
 $x, y$
with
$x, y$
with
 $\neg (x K y)$
can be separated by a K-saturated clopen set.
$\neg (x K y)$
can be separated by a K-saturated clopen set. -
(2)
 $RK \subseteq KR$
(K is correct with respect to R);
$RK \subseteq KR$
(K is correct with respect to R); -
(3)
 $EK \subseteq KE$
or, equivalently,
$EK \subseteq KE$
or, equivalently,
 $EK = KE$
(K is correct with respect to E).
$EK = KE$
(K is correct with respect to E).
The quotient
![]() $\mathfrak {F}/K$
is defined to be
$\mathfrak {F}/K$
is defined to be
![]() $(X/K, \overline {R}, \overline {E})$
, where
$(X/K, \overline {R}, \overline {E})$
, where
![]() $\alpha \overline {R} \beta $
iff
$\alpha \overline {R} \beta $
iff
![]() $\exists x \in \alpha , y \in \beta : x R y$
(or, equivalently,
$\exists x \in \alpha , y \in \beta : x R y$
(or, equivalently,
![]() $\forall x \in \alpha , \exists y \in \beta : x R y$
), and
$\forall x \in \alpha , \exists y \in \beta : x R y$
), and
![]() $\overline {E}$
is defined similarly.
$\overline {E}$
is defined similarly.
Correct partitions are the kernels of continuous p-morphisms. Hence, by standard duality theory (as outlined in Remark 2.14), the lattice of correct partitions of
![]() $\mathfrak {F}$
ordered by inclusion is dually isomorphic to the lattice of subalgebras of
$\mathfrak {F}$
ordered by inclusion is dually isomorphic to the lattice of subalgebras of
![]() $\mathfrak {F}^*$
.
$\mathfrak {F}^*$
.
Remark 5.6. As noted in the previous definition, when a partition K is correct with respect to the equivalence relation E, the relations actually commute and we have
![]() $EK = KE$
. Thus, not only does E give rise to an equivalence relation
$EK = KE$
. Thus, not only does E give rise to an equivalence relation
![]() $\overline {E}$
on K-classes, but K also gives rise to an equivalence relation on E-classes, which we denote by
$\overline {E}$
on K-classes, but K also gives rise to an equivalence relation on E-classes, which we denote by
![]() $\overline {K}$
. In particular, two E-classes are
$\overline {K}$
. In particular, two E-classes are
![]() $\overline {K}$
-related iff every member of each class is K-related to some member of the other. This idea is put to use in Theorem 5.13 and Lemma 6.12.
$\overline {K}$
-related iff every member of each class is K-related to some member of the other. This idea is put to use in Theorem 5.13 and Lemma 6.12.
We now adapt to our setting a dual characterization of finitely generated algebras; this criterion was given in the setting of
![]() $\mathsf {S4}$
-algebras and Heyting algebras in [Reference Esakia and Grigolia12], with an identical proof.
$\mathsf {S4}$
-algebras and Heyting algebras in [Reference Esakia and Grigolia12], with an identical proof.
Definition 5.7. Let
![]() $\mathfrak {F} = (X, R, E)$
be an
$\mathfrak {F} = (X, R, E)$
be an
![]() $\mathsf {MS4}$
-frame, and
$\mathsf {MS4}$
-frame, and
![]() $\overline {g} = (g_1, \dots , g_n)$
a tuple of elements of
$\overline {g} = (g_1, \dots , g_n)$
a tuple of elements of
![]() $\mathfrak {F}^*$
. Define
$\mathfrak {F}^*$
. Define
-
(1) the coloring
 $c_{\bar {g}} : X \to 2^n$
by
$c_{\bar {g}} : X \to 2^n$
by  $$\begin{align*}c_{\bar{g}}(x)(i) = \begin{cases} 1 & x \in g_i, \\ 0 & \text{otherwise}; \end{cases} \end{align*}$$
$$\begin{align*}c_{\bar{g}}(x)(i) = \begin{cases} 1 & x \in g_i, \\ 0 & \text{otherwise}; \end{cases} \end{align*}$$
-
(2) the relation
 $C_{\bar {g}} \subseteq X^2$
as the kernel of
$C_{\bar {g}} \subseteq X^2$
as the kernel of
 $c_{\bar {g}}$
, i.e.,
$c_{\bar {g}}$
, i.e.,
 $x C_{\bar {g}} y$
iff
$x C_{\bar {g}} y$
iff
 $c_{\bar {g}}(x) = c_{\bar {g}}(y)$
.
$c_{\bar {g}}(x) = c_{\bar {g}}(y)$
.
We call
![]() $c_{\bar {g}}$
the coloring and
$c_{\bar {g}}$
the coloring and
![]() $C_{\bar {g}}$
the partition induced by
$C_{\bar {g}}$
the partition induced by
![]() $\bar {g}$
. We will commonly drop the subscript
$\bar {g}$
. We will commonly drop the subscript
![]() $\bar {g}$
when unambiguous.
$\bar {g}$
when unambiguous.
We call an equivalence relation K on X non-trivial if it relates two distinct elements of X (i.e., it is strictly above the diagonal in the lattice of equivalence relations).
Theorem 5.8 (Coloring theorem).
Let
![]() $\mathfrak {F}$
be a descriptive
$\mathfrak {F}$
be a descriptive
![]() $\mathsf {MS4}$
-frame, and
$\mathsf {MS4}$
-frame, and
![]() $\bar {g} = (g_1, \dots , g_n)$
a tuple of elements of
$\bar {g} = (g_1, \dots , g_n)$
a tuple of elements of
![]() $\mathfrak {F}^*$
. Then
$\mathfrak {F}^*$
. Then
![]() $\mathfrak {F}^*$
is not generated by
$\mathfrak {F}^*$
is not generated by
![]() $\overline {g}$
iff there exists a non-trivial correct partition K of
$\overline {g}$
iff there exists a non-trivial correct partition K of
![]() $\mathfrak {F}$
with
$\mathfrak {F}$
with
![]() $K \subseteq C$
(that is, each class of K contains only points of the same color).
$K \subseteq C$
(that is, each class of K contains only points of the same color).
Proof. Suppose
![]() $\mathfrak {F}^*$
is generated by
$\mathfrak {F}^*$
is generated by
![]() $\bar {g}$
, and let K be a non-trivial correct partition. Then K corresponds to a proper subalgebra of
$\bar {g}$
, and let K be a non-trivial correct partition. Then K corresponds to a proper subalgebra of
![]() $\mathfrak {F}^*$
that couldn’t contain all of the
$\mathfrak {F}^*$
that couldn’t contain all of the
![]() $g_i$
. That is, there is some
$g_i$
. That is, there is some
![]() $g_i$
that is not K-saturated. So there are
$g_i$
that is not K-saturated. So there are
![]() $x \in g_i$
and
$x \in g_i$
and
![]() $y \not \in g_i$
that are K-related. Thus,
$y \not \in g_i$
that are K-related. Thus,
![]() $xKy$
but
$xKy$
but
![]() $c(x) \neq c(y)$
, and we’ve shown that any non-trivial correct partition K cannot satisfy
$c(x) \neq c(y)$
, and we’ve shown that any non-trivial correct partition K cannot satisfy
![]() $K \subseteq C$
.
$K \subseteq C$
.
Now suppose
![]() $\mathfrak {F}^*$
is not generated by
$\mathfrak {F}^*$
is not generated by
![]() $\bar {g}$
. Then
$\bar {g}$
. Then
![]() $\bar {g}$
generates a proper subalgebra
$\bar {g}$
generates a proper subalgebra
![]() $\mathfrak {A}$
, which gives rise to a non-trivial correct partition K, defined by
$\mathfrak {A}$
, which gives rise to a non-trivial correct partition K, defined by
Now, if
![]() $c(x) \neq c(y)$
, then
$c(x) \neq c(y)$
, then
![]() $x \in g_i$
and
$x \in g_i$
and
![]() $y \in\ -g_i$
for some
$y \in\ -g_i$
for some
![]() $g_i \in \mathfrak {A}$
, so
$g_i \in \mathfrak {A}$
, so
![]() $\neg (xKy)$
. Thus,
$\neg (xKy)$
. Thus,
![]() $K \subseteq C$
.
$K \subseteq C$
.
Remark 5.9. The previous definition and theorem hold more generally (with the same proof) for any boolean algebra with unary operators or, dually, any descriptive frame with binary relations.
With all the tools we need, we are now ready to give an explicit description of the
![]() $\mathsf {MS4}$
-frame that is the dual frame of the Erdös–Tarski algebra.
$\mathsf {MS4}$
-frame that is the dual frame of the Erdös–Tarski algebra.
Example 5.10. Let
![]() $\mathfrak {F} = (X, E_1, E_2)$
where
$\mathfrak {F} = (X, E_1, E_2)$
where
The equivalence classes of
![]() $E_1$
are rows, the equivalence classes of
$E_1$
are rows, the equivalence classes of
![]() $E_2$
are columns, and
$E_2$
are columns, and
![]() $k_1, k_2 \in E_1(0, \omega ) \cap E_2(\omega , 0)$
(so that
$k_1, k_2 \in E_1(0, \omega ) \cap E_2(\omega , 0)$
(so that
![]() $\left \{k_1, k_2\right \}$
is the only non-trivial equivalence class of
$\left \{k_1, k_2\right \}$
is the only non-trivial equivalence class of
![]() $E_1 \cap E_2$
); see Figure 3.
$E_1 \cap E_2$
); see Figure 3.

Figure 3 Descriptive frame of Example 5.10.
In the remainder of the section, we demonstrate that
![]() $\mathfrak {F}$
has the desired properties. To define the topology on X, we will describe it as a two-point compactification of the space
$\mathfrak {F}$
has the desired properties. To define the topology on X, we will describe it as a two-point compactification of the space
![]() $X_0 = (\omega + 1 \times \omega + 1) - \left \{(\omega , \omega )\right \}$
, where
$X_0 = (\omega + 1 \times \omega + 1) - \left \{(\omega , \omega )\right \}$
, where
![]() $\omega + 1$
has the usual interval topology, and
$\omega + 1$
has the usual interval topology, and
![]() $X_0$
has its usual topology of a subspace of the product. As an open subset of a Stone space,
$X_0$
has its usual topology of a subspace of the product. As an open subset of a Stone space,
![]() $X_0$
is zero-dimensional, locally compact, and Hausdorff (that is,
$X_0$
is zero-dimensional, locally compact, and Hausdorff (that is,
![]() $X_0$
is locally Stone). Define
$X_0$
is locally Stone). Define
Note that
![]() $g_1$
and
$g_1$
and
![]() $g_2$
are disjoint clopen sets that are neither compact nor co-compact (i.e., having a compact complement) in
$g_2$
are disjoint clopen sets that are neither compact nor co-compact (i.e., having a compact complement) in
![]() $X_0$
. In the terminology of [Reference Magill24, Definition 2.2],
$X_0$
. In the terminology of [Reference Magill24, Definition 2.2],
![]() $\left \{g_1, g_2\right \}$
is a 2-star in
$\left \{g_1, g_2\right \}$
is a 2-star in
![]() $X_0$
—a pair of disjoint open sets with the property that the complement of their union is compact but the complement of each set itself is not. In [Reference Magill24, Theorem 2.1] it is shown that this datum gives rise to a 2-point compactification of
$X_0$
—a pair of disjoint open sets with the property that the complement of their union is compact but the complement of each set itself is not. In [Reference Magill24, Theorem 2.1] it is shown that this datum gives rise to a 2-point compactification of
![]() $X_0$
; specifically, we have the following basis for a compact Hausdorff topology on X:
$X_0$
; specifically, we have the following basis for a compact Hausdorff topology on X:
(Note that
![]() $\mathcal {B}$
is not a clopen basis.)
$\mathcal {B}$
is not a clopen basis.)
Lemma 5.11. X is a Stone space.
Proof. By [Reference Magill24, Theorem 2.1], X is compact Hausdorff. We show that X is zero-dimensional. For this it suffices to separate distinct points of X by a clopen subset of X (see, e.g., [Reference Johnstone19, p. 69]). First suppose that
![]() $x, y \in X_0$
. Since
$x, y \in X_0$
. Since
![]() $X_0$
is zero-dimensional, there is a clopen set
$X_0$
is zero-dimensional, there is a clopen set
![]() $U\subseteq X_0$
containing x and missing y. Because
$U\subseteq X_0$
containing x and missing y. Because
![]() $X_0$
is locally compact, x has a compact neighborhood K in
$X_0$
is locally compact, x has a compact neighborhood K in
![]() $X_0$
. Therefore, there is a clopen set V with
$X_0$
. Therefore, there is a clopen set V with
![]() $x\in V \subseteq U\cap K$
. But then V is a compact clopen of
$x\in V \subseteq U\cap K$
. But then V is a compact clopen of
![]() $X_0$
, and hence a clopen subset of X separating x and y. The points
$X_0$
, and hence a clopen subset of X separating x and y. The points
![]() $k_1$
and
$k_1$
and
![]() $k_2$
are separated by
$k_2$
are separated by
![]() $g_1 \cup \left \{k_1\right \}$
which is clopen of X by definition. Finally,
$g_1 \cup \left \{k_1\right \}$
which is clopen of X by definition. Finally,
![]() $x \in X_0$
and
$x \in X_0$
and
![]() $k_i$
are separated by any compact clopen neighborhood K of x in
$k_i$
are separated by any compact clopen neighborhood K of x in
![]() $X_0$
, which is a clopen set of X.
$X_0$
, which is a clopen set of X.
Lemma 5.12.
![]() $\mathfrak {F}$
is a descriptive
$\mathfrak {F}$
is a descriptive
![]() $\mathsf {S5}^2$
-frame.
$\mathsf {S5}^2$
-frame.
Proof. Since X is a Stone space by the above lemma, it remains to show that
![]() $E_1, E_2$
are continuous. We show that
$E_1, E_2$
are continuous. We show that
![]() $E_1$
is continuous. The proof for
$E_1$
is continuous. The proof for
![]() $E_2$
is symmetric. Observe that all finite-index rows (i.e.,
$E_2$
is symmetric. Observe that all finite-index rows (i.e.,
![]() $[0, \omega ] \times \left \{j\right \}$
for
$[0, \omega ] \times \left \{j\right \}$
for
![]() $j < \omega $
) are evidently clopen, while the “top row”
$j < \omega $
) are evidently clopen, while the “top row”
![]() $\left \{(i, \omega ) : i < \omega \right \} \cup \left \{k_1,k_2\right \}$
is closed but not open (its complement is the union of all finite-index rows). Hence,
$\left \{(i, \omega ) : i < \omega \right \} \cup \left \{k_1,k_2\right \}$
is closed but not open (its complement is the union of all finite-index rows). Hence,
![]() $E_1$
is point-closed.
$E_1$
is point-closed.
It is left to show that U clopen implies
![]() $E_1(U)$
is clopen. By [Reference Esakia, Bezhanishvili and Holliday13, Theorem 3.1.2(IV)], it is enough to verify the following two conditions:
$E_1(U)$
is clopen. By [Reference Esakia, Bezhanishvili and Holliday13, Theorem 3.1.2(IV)], it is enough to verify the following two conditions:
-
(1) If
 $y \not \in E_1(x)$
, then there is a partition into two
$y \not \in E_1(x)$
, then there is a partition into two
 $E_1$
-saturated open sets separating x and y.
$E_1$
-saturated open sets separating x and y. -
(2) For all x and open V, if
 $E_1(x) \cap V \neq \varnothing $
, then there is an open neighborhood U of x with
$E_1(x) \cap V \neq \varnothing $
, then there is an open neighborhood U of x with
 $E_1(y) \cap V \neq \varnothing $
for all
$E_1(y) \cap V \neq \varnothing $
for all
 $y \in U$
.
$y \in U$
.
For (1), since
![]() $y \not \in E_1(x)$
, x and y are in distinct rows. Therefore, one of them must be in a row of finite index, say
$y \not \in E_1(x)$
, x and y are in distinct rows. Therefore, one of them must be in a row of finite index, say
![]() $R_n = [0,\omega ] \times \{ n \}$
with
$R_n = [0,\omega ] \times \{ n \}$
with
![]() $n < \omega $
(if both are in rows of finite index, take n to be the least index). Then
$n < \omega $
(if both are in rows of finite index, take n to be the least index). Then
![]() $[0, \omega]$
and its complement provide a partition of X into two
$[0, \omega]$
and its complement provide a partition of X into two
![]() $E_1$
-saturated open sets separating x and y.
$E_1$
-saturated open sets separating x and y.
For (2), we consider cases: If
![]() $x = (i, j)$
for
$x = (i, j)$
for
![]() $i, j < \omega $
,
$i, j < \omega $
,
![]() $\left \{x\right \}$
is an appropriate neighborhood. If
$\left \{x\right \}$
is an appropriate neighborhood. If
![]() $x = (\omega , j)$
for
$x = (\omega , j)$
for
![]() $j < \omega $
, then
$j < \omega $
, then
![]() $[0,\omega ] \times \left \{j\right \}$
is an appropriate neighborhood. Suppose
$[0,\omega ] \times \left \{j\right \}$
is an appropriate neighborhood. Suppose
![]() $x = (i, \omega )$
for
$x = (i, \omega )$
for
![]() $i<\omega $
. If
$i<\omega $
. If
![]() $E_1(x) \cap V$
contains
$E_1(x) \cap V$
contains
![]() $(i', \omega )$
for
$(i', \omega )$
for
![]() $i'<\omega $
, then V contains a neighborhood
$i'<\omega $
, then V contains a neighborhood
![]() $\left \{i'\right \} \times [n, \omega ]$
for
$\left \{i'\right \} \times [n, \omega ]$
for
![]() $n < \omega $
, so
$n < \omega $
, so
![]() $\left \{i\right \} \times [n, \omega ]$
is an appropriate neighborhood of x. If
$\left \{i\right \} \times [n, \omega ]$
is an appropriate neighborhood of x. If
![]() $E_1(x) \cap V$
contains
$E_1(x) \cap V$
contains
![]() $k_1$
, then V contains some
$k_1$
, then V contains some
![]() $V' \cup \left \{k_1\right \}$
with
$V' \cup \left \{k_1\right \}$
with
![]() $g_1 - V'$
compact in
$g_1 - V'$
compact in
![]() $X_0$
, as sets of this form are the only basic open neighborhoods of
$X_0$
, as sets of this form are the only basic open neighborhoods of
![]() $k_1$
. Then there must be some n with
$k_1$
. Then there must be some n with
![]() $(g_1- V')\cap [n, \omega ]^2 = \varnothing $
(indeed any
$(g_1- V')\cap [n, \omega ]^2 = \varnothing $
(indeed any
![]() $U \subseteq X_0$
compact has this property since otherwise
$U \subseteq X_0$
compact has this property since otherwise
![]() $\left \{X_0-[n, \omega ]^2 : n < \omega \right \}$
would be an open cover of U without a finite subcover). Therefore,
$\left \{X_0-[n, \omega ]^2 : n < \omega \right \}$
would be an open cover of U without a finite subcover). Therefore,
![]() $g_1 \cap [n, \omega ]^2 \subseteq V' \subseteq V$
, and again
$g_1 \cap [n, \omega ]^2 \subseteq V' \subseteq V$
, and again
![]() $\left \{i\right \} \times [n, \omega ]$
is an appropriate neighborhood of x. If
$\left \{i\right \} \times [n, \omega ]$
is an appropriate neighborhood of x. If
![]() $E_1(x) \cap V$
contains
$E_1(x) \cap V$
contains
![]() $k_2$
, then by the same argument we have an n with
$k_2$
, then by the same argument we have an n with
![]() $g_2 \cap [n, \omega ]^2 \subseteq V$
and the same neighborhood works. Finally, suppose
$g_2 \cap [n, \omega ]^2 \subseteq V$
and the same neighborhood works. Finally, suppose
![]() $x = k_s$
for
$x = k_s$
for
![]() $s \in \left \{1,2\right \}$
. If
$s \in \left \{1,2\right \}$
. If
![]() $E_1(x) \cap V$
contains
$E_1(x) \cap V$
contains
![]() $(i, \omega )$
for
$(i, \omega )$
for
![]() $i < \omega $
, then V contains
$i < \omega $
, then V contains
![]() $\left \{i\right \} \times [n, \omega ]$
for some n, and
$\left \{i\right \} \times [n, \omega ]$
for some n, and
![]() $(g_s \cap [n, \omega ]^2) \cup \left \{k_s\right \}$
is an appropriate basic open neighborhood of x. If
$(g_s \cap [n, \omega ]^2) \cup \left \{k_s\right \}$
is an appropriate basic open neighborhood of x. If
![]() $E_1(x) \cap V$
contains
$E_1(x) \cap V$
contains
![]() $k_t$
for
$k_t$
for
![]() $t \neq s$
, then by the same argument as before we have
$t \neq s$
, then by the same argument as before we have
![]() $g_t \cap [n, \omega ]^2 \subseteq V$
for some n, and the same neighborhood
$g_t \cap [n, \omega ]^2 \subseteq V$
for some n, and the same neighborhood
![]() $(g_s \cap [n, \omega]^2) \cup \{k_s\}$
works.
$(g_s \cap [n, \omega]^2) \cup \{k_s\}$
works.
Theorem 5.13.
![]() $\mathfrak {F}$
is one-generated and
$\mathfrak {F}$
is one-generated and
![]() $\mathfrak {F}^*$
is isomorphic to the Erdös–Tarski algebra.
$\mathfrak {F}^*$
is isomorphic to the Erdös–Tarski algebra.
Proof. Let
![]() $g = g_1 \cup \left \{k_1\right \}$
(see Figure 3). We claim
$g = g_1 \cup \left \{k_1\right \}$
(see Figure 3). We claim
![]() $\mathfrak {F}^* = \langle g \rangle $
. Suppose not. By the coloring theorem, there exists a non-trivial correct partition K of X such that every class of K is contained in g or
$\mathfrak {F}^* = \langle g \rangle $
. Suppose not. By the coloring theorem, there exists a non-trivial correct partition K of X such that every class of K is contained in g or
![]() ${-}g$
. Since it is non-trivial, K must identify two points in distinct rows or columns (by assumption we cannot have
${-}g$
. Since it is non-trivial, K must identify two points in distinct rows or columns (by assumption we cannot have
![]() $k_1 K k_2$
). By Remark 5.6, this is to say that two distinct rows or columns must be
$k_1 K k_2$
). By Remark 5.6, this is to say that two distinct rows or columns must be
![]() $\overline {K}$
-related. Let
$\overline {K}$
-related. Let
![]() $C_i = \left \{i\right \} \times [0, \omega ]$
be the i-th column and
$C_i = \left \{i\right \} \times [0, \omega ]$
be the i-th column and
![]() $R_j = [0, \omega ] \times \left \{j\right \}$
the j-th row. Observe that
$R_j = [0, \omega ] \times \left \{j\right \}$
the j-th row. Observe that
![]() $C_0$
cannot be related to
$C_0$
cannot be related to
![]() $C_i$
for
$C_i$
for
![]() $i> 0$
since otherwise a point in
$i> 0$
since otherwise a point in
![]() ${-}g \cap C_i$
would be K-related to a point in
${-}g \cap C_i$
would be K-related to a point in
![]() ${-}g \cap C_0 = \varnothing $
.
${-}g \cap C_0 = \varnothing $
.
Now suppose
![]() $C_{i_1}$
and
$C_{i_1}$
and
![]() $C_{i_2}$
are
$C_{i_2}$
are
![]() $\overline {K}$
-related for
$\overline {K}$
-related for
![]() $0 < i_1 < i_2 \leq \omega $
. Then there must be some
$0 < i_1 < i_2 \leq \omega $
. Then there must be some
![]() $j_2 \in [i_1, i_2)$
so that
$j_2 \in [i_1, i_2)$
so that
![]() $(i_2, j_2) K (i_1, j_1)$
for some
$(i_2, j_2) K (i_1, j_1)$
for some
![]() $j_1 \in [0, i_1)$
(since all points in
$j_1 \in [0, i_1)$
(since all points in
![]() ${-}g \cap C_{i_2}$
must be K-related to points in
${-}g \cap C_{i_2}$
must be K-related to points in
![]() ${-}g \cap C_{i_1}$
). Therefore, rows
${-}g \cap C_{i_1}$
). Therefore, rows
![]() $j_1$
and
$j_1$
and
![]() $j_2$
are
$j_2$
are
![]() $\overline {K}$
-related, with
$\overline {K}$
-related, with
![]() $0 \leq j_1 < j_2 < i_2$
. Thus,
$0 \leq j_1 < j_2 < i_2$
. Thus,
![]() $(j_2, j_2) K (i_0, j_1)$
for some
$(j_2, j_2) K (i_0, j_1)$
for some
![]() $i_0 \in [0, j_1]$
. We now conclude that columns
$i_0 \in [0, j_1]$
. We now conclude that columns
![]() $i_0$
and
$i_0$
and
![]() $j_2$
are
$j_2$
are
![]() $\overline {K}$
-related, and note that
$\overline {K}$
-related, and note that
![]() $0 \leq i_0 < i_1$
,
$0 \leq i_0 < i_1$
,
![]() $0 < j_2 < i_2$
, and
$0 < j_2 < i_2$
, and
![]() $i_0 < j_2$
. So from our assumption of two
$i_0 < j_2$
. So from our assumption of two
![]() $\overline {K}$
-related columns, we have found two
$\overline {K}$
-related columns, we have found two
![]() $\overline {K}$
-related columns of strictly lower index, and iterating this process will eventually reveal that column
$\overline {K}$
-related columns of strictly lower index, and iterating this process will eventually reveal that column
![]() $0$
must be
$0$
must be
![]() $\overline {K}$
-related to some non-zero column, which is a contradiction by the previous paragraph.
$\overline {K}$
-related to some non-zero column, which is a contradiction by the previous paragraph.
Finally, suppose
![]() $R_{j_1}$
and
$R_{j_1}$
and
![]() $R_{j_2}$
are
$R_{j_2}$
are
![]() $\overline {K}$
-related for
$\overline {K}$
-related for
![]() $0 \leq j_1 < j_2 \leq \omega $
. Then
$0 \leq j_1 < j_2 \leq \omega $
. Then
![]() $(j_2, j_2) K (i, j_1)$
(or
$(j_2, j_2) K (i, j_1)$
(or
![]() $k_1 K (i, j_1)$
in the case
$k_1 K (i, j_1)$
in the case
![]() $j_2 = \omega $
) for some
$j_2 = \omega $
) for some
![]() $i \in [0, j_1]$
. But then columns i and
$i \in [0, j_1]$
. But then columns i and
![]() $j_2$
are
$j_2$
are
![]() $\overline {K}$
-related, with
$\overline {K}$
-related, with
![]() $i < j_2$
, which is a contradiction by the last paragraph.
$i < j_2$
, which is a contradiction by the last paragraph.
Consequently, such a K cannot exist, and we conclude that
![]() $\mathfrak {F}^*$
is generated by g. There is an evident homomorphism
$\mathfrak {F}^*$
is generated by g. There is an evident homomorphism
![]() $f : \mathfrak {F}^* \to \mathcal {P}(\omega \times \omega )$
given by
$f : \mathfrak {F}^* \to \mathcal {P}(\omega \times \omega )$
given by
![]() $U \mapsto U \cap (\omega \times \omega )$
. Then
$U \mapsto U \cap (\omega \times \omega )$
. Then
![]() $f(g) = \left \{(i, j) : i \leq j\right \}$
, and f is an isomorphism onto its image (because
$f(g) = \left \{(i, j) : i \leq j\right \}$
, and f is an isomorphism onto its image (because
![]() $\omega \times \omega $
is dense in X). Thus,
$\omega \times \omega $
is dense in X). Thus,
![]() $\mathfrak{F}^*$
is isomorphic to the subalgebra of
$\mathfrak{F}^*$
is isomorphic to the subalgebra of
![]() $\mathcal{P}(\omega \times \omega)$
generated by
$\mathcal{P}(\omega \times \omega)$
generated by
![]() $f(g)$
, which is exactly the Erdös–Tarski algebra.
$f(g)$
, which is exactly the Erdös–Tarski algebra.
This provides an example of a descriptive
![]() $\mathsf {MS4}[1]$
-frame whose (only) layer is infinite and contains limit points. Thus, the only part of Theorem 5.3 that has a hope to be salvaged in the monadic setting is that each layer may be clopen.
$\mathsf {MS4}[1]$
-frame whose (only) layer is infinite and contains limit points. Thus, the only part of Theorem 5.3 that has a hope to be salvaged in the monadic setting is that each layer may be clopen.
Question 5.14. Let
![]() $(X, R, E)$
be a finitely generated descriptive
$(X, R, E)$
be a finitely generated descriptive
![]() $\mathsf {MS4}$
-frame. Is
$\mathsf {MS4}$
-frame. Is
![]() $D_1 = \max X$
or any
$D_1 = \max X$
or any
![]() $D_n$
a clopen (admissible, definable) set?
$D_n$
a clopen (admissible, definable) set?
Question 5.15. Does there exist a finitely generated descriptive
![]() $\mathsf {MS4}$
-frame whose finite layers consist only of limit points?
$\mathsf {MS4}$
-frame whose finite layers consist only of limit points?
6 Translating
 $\mathbf {S5}_2$
to
$\mathbf {S5}_2$
to
 $\mathbf {MS4_S}[2]$
$\mathbf {MS4_S}[2]$
In this section we follow up on the promise made at the end of Section 4 and give a semantic translation from subvarieties of
![]() $\mathbf {S5}_2$
to subvarieties of
$\mathbf {S5}_2$
to subvarieties of
![]() $\mathbf {MS4_S}[2]$
that preserves and reflects local finiteness. Before doing so, we develop some basic facts about the variety of
$\mathbf {MS4_S}[2]$
that preserves and reflects local finiteness. Before doing so, we develop some basic facts about the variety of
![]() $\mathsf {S5}_2$
-algebras and their dual frames.
$\mathsf {S5}_2$
-algebras and their dual frames.
Definition 6.1 [Reference Gabbay, Kurucz, Wolter and Zakharyaschev15, Section 3.1].
The logic
![]() $\mathsf {S5}_2$
is the fusion
$\mathsf {S5}_2$
is the fusion
![]() $\mathsf {S5} \oplus \mathsf {S5}$
, i.e., the smallest normal modal logic in the language with two modalities
$\mathsf {S5} \oplus \mathsf {S5}$
, i.e., the smallest normal modal logic in the language with two modalities
![]() $\exists _1$
and
$\exists _1$
and
![]() $\exists _2$
containing the
$\exists _2$
containing the
![]() $\mathsf {S5}$
axioms for each
$\mathsf {S5}$
axioms for each
![]() $\exists _i$
(and no other axioms).
$\exists _i$
(and no other axioms).
Algebraic models of
![]() $\mathsf {S5}_2$
are triples
$\mathsf {S5}_2$
are triples
![]() $(B, \exists _1, \exists _2)$
, where
$(B, \exists _1, \exists _2)$
, where
![]() $(B, \exists _i)$
is an
$(B, \exists _i)$
is an
![]() $\mathsf {S5}$
-algebra for
$\mathsf {S5}$
-algebra for
![]() $i = 1,2$
. We call such algebras
$i = 1,2$
. We call such algebras
![]() $\mathsf {S5}_2$
-algebras. Jónsson–Tarski duality specializes to yield that the corresponding variety
$\mathsf {S5}_2$
-algebras. Jónsson–Tarski duality specializes to yield that the corresponding variety
![]() $\mathbf {S5}_2$
is dually equivalent to the following category of descriptive frames.
$\mathbf {S5}_2$
is dually equivalent to the following category of descriptive frames.
Definition 6.2. A descriptive
![]() $\mathsf {S5}_2$
-frame is a triple
$\mathsf {S5}_2$
-frame is a triple
![]() $\mathfrak {F} = (X, E_1, E_2)$
where X is a Stone space and
$\mathfrak {F} = (X, E_1, E_2)$
where X is a Stone space and
![]() $E_1,E_2$
are two continuous equivalence relations on X (see Definition 2.8).
$E_1,E_2$
are two continuous equivalence relations on X (see Definition 2.8).
An
![]() $\mathsf {S5}_2$
-morphism between descriptive
$\mathsf {S5}_2$
-morphism between descriptive
![]() $\mathsf {S5}_2$
-frames is a continuous map
$\mathsf {S5}_2$
-frames is a continuous map
![]() $f:(X, E_1, E_2) \to (X', E_1', E_2')$
that is a p-morphism with respect to both
$f:(X, E_1, E_2) \to (X', E_1', E_2')$
that is a p-morphism with respect to both
![]() $(E_1,E_1')$
and
$(E_1,E_1')$
and
![]() $(E_2,E_2')$
. When we depict
$(E_2,E_2')$
. When we depict
![]() $\mathsf {S5}_2$
-frames, we will depict
$\mathsf {S5}_2$
-frames, we will depict
![]() $E_1$
-equivalence classes as horizontal lines and
$E_1$
-equivalence classes as horizontal lines and
![]() $E_2$
-equivalence classes with vertical analogues.
$E_2$
-equivalence classes with vertical analogues.
Definition 6.3.
-
(1) For an
 $\mathsf {S5}_2$
-algebra
$\mathsf {S5}_2$
-algebra
 $(B, \exists _1, \exists _2)$
, define
$(B, \exists _1, \exists _2)$
, define
 $\diamondsuit = \exists _1 \vee \exists _2$
.
$\diamondsuit = \exists _1 \vee \exists _2$
. -
(2) For an
 $\mathsf {S5}_2$
-frame
$\mathsf {S5}_2$
-frame
 $(X, E_1, E_2)$
, define
$(X, E_1, E_2)$
, define
 $S = E_1 \cup E_2$
.
$S = E_1 \cup E_2$
.
It is straightforward to see that S is a reflexive and symmetric relation (or edge relation) on X and that S is the dual relation of
![]() $\diamondsuit $
. Hence,
$\diamondsuit $
. Hence,
![]() $\diamondsuit $
is a possibility operator validating the well-known
$\diamondsuit $
is a possibility operator validating the well-known
![]() $\mathsf {T}$
and
$\mathsf {T}$
and
![]() $\mathsf {B}$
axioms, making it a
$\mathsf {B}$
axioms, making it a
![]() $\mathsf {KTB}$
-modality. We write
$\mathsf {KTB}$
-modality. We write
![]() $S^* = \bigcup _{n=0}^\infty S^n$
for the reflexive transitive closure of S.
$S^* = \bigcup _{n=0}^\infty S^n$
for the reflexive transitive closure of S.
Definition 6.4 [Reference Venema33].
Let
![]() $\mathfrak {F} = (X, E_1, E_2)$
be a descriptive
$\mathfrak {F} = (X, E_1, E_2)$
be a descriptive
![]() $\mathsf {S5}_2$
-frame.
$\mathsf {S5}_2$
-frame.
-
(1) Call
 $x \in X$
a topo-root of
$x \in X$
a topo-root of
 $\mathfrak {F}$
if
$\mathfrak {F}$
if
 $S^*(x)$
is dense in X.
$S^*(x)$
is dense in X. -
(2) We say that
 $\mathfrak {F}$
is topo-rooted if it has a topo-root, and strongly topo-rooted if it has an open set of topo-roots.
$\mathfrak {F}$
is topo-rooted if it has a topo-root, and strongly topo-rooted if it has an open set of topo-roots.
The following is a consequence of general results in [Reference Venema33].
Theorem 6.5. Let
![]() $\mathfrak {A}$
be an
$\mathfrak {A}$
be an
![]() $\mathsf {S5}_2$
-algebra.
$\mathsf {S5}_2$
-algebra.
-
(1)
 $\mathfrak {A}$
is s.i. iff
$\mathfrak {A}$
is s.i. iff
 $\mathfrak {A}_*$
is strongly topo-rooted.
$\mathfrak {A}_*$
is strongly topo-rooted. -
(2)
 $\mathfrak {A}$
is simple iff every point of
$\mathfrak {A}$
is simple iff every point of
 $\mathfrak {A}_*$
is a topo-root.
$\mathfrak {A}_*$
is a topo-root.
Following [Reference Rautenberg28] (see also [Reference Kracht23, p. 74]), we call a variety
![]() $\mathbf {V} \subseteq \mathbf {S5}_2$
n-transitive if
$\mathbf {V} \subseteq \mathbf {S5}_2$
n-transitive if
![]() $\mathbf {V} \models \diamondsuit ^{n+1} a \leq \diamondsuit ^n a$
, and weakly transitive if it is n-transitive for some
$\mathbf {V} \models \diamondsuit ^{n+1} a \leq \diamondsuit ^n a$
, and weakly transitive if it is n-transitive for some
![]() $n < \omega $
. The following is a consequence of a more general result of Kowalski and Kracht [Reference Kowalski and Kracht21, Theorem 12] (note that
$n < \omega $
. The following is a consequence of a more general result of Kowalski and Kracht [Reference Kowalski and Kracht21, Theorem 12] (note that
![]() $\mathbf {S5}_2$
is automatically cyclic since each basic modality is
$\mathbf {S5}_2$
is automatically cyclic since each basic modality is
![]() $\mathsf {S5}$
, see [Reference Kowalski and Kracht21, Proposition 6]).
$\mathsf {S5}$
, see [Reference Kowalski and Kracht21, Proposition 6]).
Theorem 6.6. A variety
![]() $\mathbf {V} \subseteq \mathbf {S5}_2$
is semisimple iff it is weakly transitive.
$\mathbf {V} \subseteq \mathbf {S5}_2$
is semisimple iff it is weakly transitive.
It is a consequence of [Reference Venema33, Corollary 1] (where weak transitivity goes by the name of
![]() $\omega $
-transitivity) that in a weakly transitive variety of
$\omega $
-transitivity) that in a weakly transitive variety of
![]() $\mathsf {S5}_2$
-algebras, roots and topo-roots coincide (where x is a root of
$\mathsf {S5}_2$
-algebras, roots and topo-roots coincide (where x is a root of
![]() $\mathfrak{F}$
if
$\mathfrak{F}$
if
![]() $S^*(x) = X$
); together with the previous theorem, this yields:
$S^*(x) = X$
); together with the previous theorem, this yields:
Theorem 6.7. Let
![]() $\mathbf {V} \subseteq \mathbf {S5}_2$
be a weakly transitive variety. The following are equivalent:
$\mathbf {V} \subseteq \mathbf {S5}_2$
be a weakly transitive variety. The following are equivalent:
-
(1)
 $\mathfrak {A} \in \mathbf {V}$
is s.i.
$\mathfrak {A} \in \mathbf {V}$
is s.i. -
(2)
 $\mathfrak {A} \in \mathbf {V}$
is simple.
$\mathfrak {A} \in \mathbf {V}$
is simple. -
(3) Every point of
 $\mathfrak{A}_*$
is a root.
$\mathfrak{A}_*$
is a root.
We are now ready to describe our translation. We start by a construction producing a descriptive
![]() $\mathsf {MS4_S}[2]$
-frame from a descriptive
$\mathsf {MS4_S}[2]$
-frame from a descriptive
![]() $\mathsf {S5}_2$
-frame.
$\mathsf {S5}_2$
-frame.
Construction 6.8. Let
![]() $\mathfrak {F} = (X, E_1, E_2)$
be a descriptive
$\mathfrak {F} = (X, E_1, E_2)$
be a descriptive
![]() $\mathsf {S5}_2$
-frame. We let
$\mathsf {S5}_2$
-frame. We let
![]() $\mathcal {L} = X / E_2$
be the quotient space and
$\mathcal {L} = X / E_2$
be the quotient space and
![]() $\pi _{\mathcal {L}} : X \to \mathcal {L}$
the quotient map. We set
$\pi _{\mathcal {L}} : X \to \mathcal {L}$
the quotient map. We set
![]() $T(\mathfrak {F}) = (X \cup \mathcal {L}, R, E)$
, where
$T(\mathfrak {F}) = (X \cup \mathcal {L}, R, E)$
, where
-
•
 $X \cup \mathcal {L}$
is the (disjoint) union of X and
$X \cup \mathcal {L}$
is the (disjoint) union of X and
 $\mathcal {L}$
,
$\mathcal {L}$
, -
• E is the smallest equivalence on
 $X \cup \mathcal {L}$
containing
$X \cup \mathcal {L}$
containing
 $E_2$
along with
$E_2$
along with  $$\begin{align*}\left\{(x, \alpha) : x \in X, \alpha \in \mathcal{L}, x \in \alpha\right\}, \end{align*}$$
$$\begin{align*}\left\{(x, \alpha) : x \in X, \alpha \in \mathcal{L}, x \in \alpha\right\}, \end{align*}$$
-
•
 $R = E_1 \cup (X \times \mathcal {L}) \cup (\mathcal {L} \times \mathcal {L})$
.
$R = E_1 \cup (X \times \mathcal {L}) \cup (\mathcal {L} \times \mathcal {L})$
.
In the case that
![]() $\lvert\mathfrak{F}\rvert$
is finite, it follows that
$\lvert\mathfrak{F}\rvert$
is finite, it follows that
![]() $\lvert T(\mathfrak{F}) \rvert \leq 2\lvert \mathfrak{F} \rvert$
and
$\lvert T(\mathfrak{F}) \rvert \leq 2\lvert \mathfrak{F} \rvert$
and
![]() $\lvert T(\mathfrak{F})^* \rvert \leq \lvert \mathfrak{F}^* \rvert^2.$
$\lvert T(\mathfrak{F})^* \rvert \leq \lvert \mathfrak{F}^* \rvert^2.$
This construction is depicted in Figure 4. Under the definition of R,
![]() $\mathcal {L}$
becomes an R-cluster, which we think of as a “top rail”. To prove that
$\mathcal {L}$
becomes an R-cluster, which we think of as a “top rail”. To prove that
![]() $T(\mathfrak {F})$
is a descriptive
$T(\mathfrak {F})$
is a descriptive
![]() $\mathsf {MS4_S}[2]$
-frame, we need the following.
$\mathsf {MS4_S}[2]$
-frame, we need the following.

Figure 4 Constructing an
![]() $\mathsf {MS4_S}[2]$
-frame from an
$\mathsf {MS4_S}[2]$
-frame from an
![]() $\mathsf {S5}_2$
-frame. In the
$\mathsf {S5}_2$
-frame. In the
![]() $\mathsf {S5}_2$
-frame on the left,
$\mathsf {S5}_2$
-frame on the left,
![]() $E_1$
-clusters are horizontal lines while
$E_1$
-clusters are horizontal lines while
![]() $E_2$
-clusters are bold vertical lines. In the
$E_2$
-clusters are bold vertical lines. In the
![]() $\mathsf {MS4_S}[2]$
-frame on the right, R-clusters are horizontal lines, proper R-arrows are drawn with arrowheads, and E-clusters are given by the shaded rectangles.
$\mathsf {MS4_S}[2]$
-frame on the right, R-clusters are horizontal lines, proper R-arrows are drawn with arrowheads, and E-clusters are given by the shaded rectangles.
Lemma 6.9.
![]() $\pi _{\mathcal {L}}$
is a clopen map, meaning that U clopen implies
$\pi _{\mathcal {L}}$
is a clopen map, meaning that U clopen implies
![]() $\pi _{\mathcal {L}}[U]$
is clopen.
$\pi _{\mathcal {L}}[U]$
is clopen.
Proof. Suppose
![]() $U \subseteq X$
is clopen. Then
$U \subseteq X$
is clopen. Then
![]() $\pi _{\mathcal {L}}^{-1}(\pi _{\mathcal {L}}[U]) = E_2(U)$
, which is clopen by continuity of
$\pi _{\mathcal {L}}^{-1}(\pi _{\mathcal {L}}[U]) = E_2(U)$
, which is clopen by continuity of
![]() $E_2$
. Since
$E_2$
. Since
![]() $\pi _{\mathcal {L}}$
is a quotient map,
$\pi _{\mathcal {L}}$
is a quotient map,
![]() $\pi _{\mathcal {L}}[U]$
is clopen.
$\pi _{\mathcal {L}}[U]$
is clopen.
Lemma 6.10.
![]() $T(\mathfrak {F})$
is a descriptive
$T(\mathfrak {F})$
is a descriptive
![]() $\mathsf {MS4_S}[2]$
-frame; furthermore,
$\mathsf {MS4_S}[2]$
-frame; furthermore,
![]() $T(\mathfrak {F})$
is Q-rooted.
$T(\mathfrak {F})$
is Q-rooted.
Proof. Note that
![]() $E_2$
is a separated partition of X (but in general not correct with respect to
$E_2$
is a separated partition of X (but in general not correct with respect to
![]() $E_1$
in the sense of Definition 5.5) since any
$E_1$
in the sense of Definition 5.5) since any
![]() $(x, y) \not \in E_2$
can be separated by a
$(x, y) \not \in E_2$
can be separated by a
![]() $E_2$
-saturated clopen (this is a property of any continuous quasi-order; see [Reference Esakia, Bezhanishvili and Holliday13, Theorem 3.1.2]). This ensures
$E_2$
-saturated clopen (this is a property of any continuous quasi-order; see [Reference Esakia, Bezhanishvili and Holliday13, Theorem 3.1.2]). This ensures
![]() $\mathcal {L}$
is a Stone space [Reference Koppelberg, Monk and Bonnet22, Lemma 8.4]. Thus, so is
$\mathcal {L}$
is a Stone space [Reference Koppelberg, Monk and Bonnet22, Lemma 8.4]. Thus, so is
![]() $X \cup \mathcal {L}$
(the union is disjoint).
$X \cup \mathcal {L}$
(the union is disjoint).
Clopen sets in
![]() $T(\mathfrak {F})$
are of the form
$T(\mathfrak {F})$
are of the form
![]() $U \cup V$
, with U clopen in X and V clopen in
$U \cup V$
, with U clopen in X and V clopen in
![]() $\mathcal {L}$
. We have
$\mathcal {L}$
. We have
-
•
 $E(x) = E_2(x) \cup \left \{E_2(x)\right \}$
for
$E(x) = E_2(x) \cup \left \{E_2(x)\right \}$
for
 $x \in X$
;
$x \in X$
; -
•
 $E(\alpha ) = \alpha \cup \left \{\alpha \right \}$
for
$E(\alpha ) = \alpha \cup \left \{\alpha \right \}$
for
 $\alpha \in \mathcal {L}$
;
$\alpha \in \mathcal {L}$
; -
•
 $E(U \cup V) = E_2(U) \cup \pi _{\mathcal {L}}[U] \cup V \cup \pi _{\mathcal {L}}^{-1}(V)$
.
$E(U \cup V) = E_2(U) \cup \pi _{\mathcal {L}}[U] \cup V \cup \pi _{\mathcal {L}}^{-1}(V)$
.
The first two items show that E-clusters are closed. In the third item, every set on the right hand side is clopen, by continuity of
![]() $E_2$
and the fact that
$E_2$
and the fact that
![]() $\pi _{\mathcal {L}}$
is a clopen map (Lemma 6.9). Thus, E is continuous. For R, we have
$\pi _{\mathcal {L}}$
is a clopen map (Lemma 6.9). Thus, E is continuous. For R, we have
-
•
 $R(x) = E_1(x) \cup \mathcal {L}$
for
$R(x) = E_1(x) \cup \mathcal {L}$
for
 $x \in X$
;
$x \in X$
; -
•
 $R(\alpha ) = \mathcal {L}$
for
$R(\alpha ) = \mathcal {L}$
for
 $\alpha \in \mathcal {L}$
;
$\alpha \in \mathcal {L}$
; -
•
 $ R^{-1}(U \cup V) = \begin {cases} E_1(U) & V = \varnothing , \\ X \cup \mathcal {L} & \text {otherwise}. \end {cases} $
$ R^{-1}(U \cup V) = \begin {cases} E_1(U) & V = \varnothing , \\ X \cup \mathcal {L} & \text {otherwise}. \end {cases} $
By the first two items, R is point-closed, which together with the third yields that R is continuous.
Now observe that
![]() $Q = ER$
is the total relation on
$Q = ER$
is the total relation on
![]() $T(\mathfrak {F})$
(i.e.,
$T(\mathfrak {F})$
(i.e.,
![]() $Q = (X \cup \mathcal {L})^2$
) because for each
$Q = (X \cup \mathcal {L})^2$
) because for each
![]() $x\in X$
we have
$x\in X$
we have
![]() $\mathcal {L}\subseteq R(x)$
, so
$\mathcal {L}\subseteq R(x)$
, so
![]() $X \cup \mathcal {L} = ER(x)$
. Therefore, every point of
$X \cup \mathcal {L} = ER(x)$
. Therefore, every point of
![]() $T(\mathfrak {F})$
is a Q-root and, in particular,
$T(\mathfrak {F})$
is a Q-root and, in particular,
![]() $RE \subseteq ER$
. Finally,
$RE \subseteq ER$
. Finally,
![]() $T(\mathfrak {F})$
is of R-depth 2 by construction. Thus,
$T(\mathfrak {F})$
is of R-depth 2 by construction. Thus,
![]() $T(\mathfrak {F})$
is a Q-rooted descriptive
$T(\mathfrak {F})$
is a Q-rooted descriptive
![]() $\mathsf {MS4_S}[2]$
-frame.
$\mathsf {MS4_S}[2]$
-frame.
By construction,
![]() $T(\mathfrak {F})$
has exactly two layers
$T(\mathfrak {F})$
has exactly two layers
![]() $D_1 = \mathcal {L}$
and
$D_1 = \mathcal {L}$
and
![]() $D_2 = X$
. By design, we have
$D_2 = X$
. By design, we have
![]() $E \vert _{D_2} = E_2$
and
$E \vert _{D_2} = E_2$
and
![]() $R \vert _{D_2} = E_1$
. Since
$R \vert _{D_2} = E_1$
. Since
![]() $D_1, D_2$
are clopen, we can consider the relativization
$D_1, D_2$
are clopen, we can consider the relativization
where the relative complementation and modal operators are given by
The maps
![]() $a \mapsto a \cap D_i$
are Boolean homomorphisms. Considering the restrictions of R and E to each layer, we see that
$a \mapsto a \cap D_i$
are Boolean homomorphisms. Considering the restrictions of R and E to each layer, we see that
![]() $\mathfrak {A}_1$
is an
$\mathfrak {A}_1$
is an
![]() $\mathsf {S5}^2$
-algebra (and in fact belongs to a proper and hence locally finite subvariety of
$\mathsf {S5}^2$
-algebra (and in fact belongs to a proper and hence locally finite subvariety of
![]() $\mathbf {S5}^2$
), while
$\mathbf {S5}^2$
), while
![]() $\mathfrak {A}_2$
is an
$\mathfrak {A}_2$
is an
![]() $\mathsf {S5}_2$
-algebra isomorphic to
$\mathsf {S5}_2$
-algebra isomorphic to
![]() $\mathfrak {F}^*$
:
$\mathfrak {F}^*$
:
Lemma 6.11.
![]() $\mathfrak {A}_2 \cong \mathfrak {F}^*$
, and the relative operations of
$\mathfrak {A}_2 \cong \mathfrak {F}^*$
, and the relative operations of
![]() $\mathfrak {A}_2$
are definable in
$\mathfrak {A}_2$
are definable in
![]() $T(\mathfrak {F})^*$
.
$T(\mathfrak {F})^*$
.
Proof. This follows from the explicit description of
![]() $R^{-1}$
and E on clopen sets in Lemma 6.10. Also, the relative complementation and modal operators are definable using the clopen set
$R^{-1}$
and E on clopen sets in Lemma 6.10. Also, the relative complementation and modal operators are definable using the clopen set
![]() $D_2 \in T(\mathfrak {F})^*$
, e.g., by using precisely the definitions from the preceding paragraph.
$D_2 \in T(\mathfrak {F})^*$
, e.g., by using precisely the definitions from the preceding paragraph.
Recall from Remark 5.6 that, since
![]() $E_2$
is an equivalence, a correct partition K on
$E_2$
is an equivalence, a correct partition K on
![]() $\mathfrak {F}$
yields an equivalence relation
$\mathfrak {F}$
yields an equivalence relation
![]() $\overline {K}$
on the set
$\overline {K}$
on the set
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $E_2$
-classes of
$E_2$
-classes of
![]() $\mathfrak {F}$
.
$\mathfrak {F}$
.
Lemma 6.12. Let K be a correct partition of
![]() $\mathfrak {F}$
. Define
$\mathfrak {F}$
. Define
![]() $\widehat {K} = K \cup \overline {K}$
, a relation on
$\widehat {K} = K \cup \overline {K}$
, a relation on
![]() $T(\mathfrak {F})$
. That is,
$T(\mathfrak {F})$
. That is,
![]() $\widehat {K}$
is the relation K on
$\widehat {K}$
is the relation K on
![]() $D_2 = X$
, and the relation
$D_2 = X$
, and the relation
![]() $\overline {K}$
on
$\overline {K}$
on
![]() $D_1 = \mathcal {L}$
(and relates no points on different layers); see Figure 5.
$D_1 = \mathcal {L}$
(and relates no points on different layers); see Figure 5.
-
(1)
 $\widehat {K}$
is a correct partition of
$\widehat {K}$
is a correct partition of
 $T(\mathfrak {F})$
.
$T(\mathfrak {F})$
. -
(2)
 $T(\mathfrak {F}/K) \cong T(\mathfrak {F})/\widehat {K}$
.
$T(\mathfrak {F}/K) \cong T(\mathfrak {F})/\widehat {K}$
.

Figure 5 Lifting a correct partition of
![]() $\mathfrak {F}$
to one of
$\mathfrak {F}$
to one of
![]() $T(\mathfrak {F})$
, as in Lemma 6.12: E-classes are depicted by dotted lines (as
$T(\mathfrak {F})$
, as in Lemma 6.12: E-classes are depicted by dotted lines (as
![]() $E_2$
-classes of
$E_2$
-classes of
![]() $\mathfrak{F}$
) with the
$\mathfrak{F}$
) with the
![]() $E_2$
-class itself depicted as a solid dot above on the top rail. The correct partition
$E_2$
-class itself depicted as a solid dot above on the top rail. The correct partition
![]() $\widehat {K}$
is depicted by the shaded rectangles.
$\widehat {K}$
is depicted by the shaded rectangles.
Proof. (1) We first show
![]() $\widehat {K}$
is separated. If
$\widehat {K}$
is separated. If
![]() $x, y \in D_2$
and
$x, y \in D_2$
and
![]() $\neg (x \widehat {K} y)$
, then
$\neg (x \widehat {K} y)$
, then
![]() $\neg (x K y)$
and they can be separated by a K-saturated clopen subset of
$\neg (x K y)$
and they can be separated by a K-saturated clopen subset of
![]() $D_2$
, which is also
$D_2$
, which is also
![]() $\widehat {K}$
-saturated (since
$\widehat {K}$
-saturated (since
![]() $\widehat {K}$
relates no points in different layers). Any
$\widehat {K}$
relates no points in different layers). Any
![]() $x \in D_2$
and
$x \in D_2$
and
![]() $\alpha \in D_1$
can be separated by
$\alpha \in D_1$
can be separated by
![]() $D_2$
which is
$D_2$
which is
![]() $\widehat {K}$
-saturated by the same reason. Now suppose
$\widehat {K}$
-saturated by the same reason. Now suppose
![]() $\alpha , \beta \in D_1$
and
$\alpha , \beta \in D_1$
and
![]() $\neg (\alpha \widehat {K} \beta )$
. Then
$\neg (\alpha \widehat {K} \beta )$
. Then
![]() $\neg (x K y)$
for any
$\neg (x K y)$
for any
![]() $x \in \alpha , y \in \beta $
, and so any such
$x \in \alpha , y \in \beta $
, and so any such
![]() $x, y$
can be separated by a K-saturated clopen
$x, y$
can be separated by a K-saturated clopen
![]() $A\subseteq D_2$
. By Lemma 6.9,
$A\subseteq D_2$
. By Lemma 6.9,
![]() $\pi _{\mathcal {L}}[A]$
is a clopen subset of
$\pi _{\mathcal {L}}[A]$
is a clopen subset of
![]() $D_1$
separating
$D_1$
separating
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. To see it is
$\beta $
. To see it is
![]() $\widehat {K}$
-saturated, let
$\widehat {K}$
-saturated, let
![]() $\gamma \in \pi _{\mathcal {L}}[A]$
and
$\gamma \in \pi _{\mathcal {L}}[A]$
and
![]() $\gamma \widehat {K} \delta $
. Then there is
$\gamma \widehat {K} \delta $
. Then there is
![]() $x \in A \cap \gamma $
and
$x \in A \cap \gamma $
and
![]() $y \in \delta $
with
$y \in \delta $
with
![]() $x K y$
(x may be chosen from A by the remarks at the end of Definition 5.5). Since A is K-saturated,
$x K y$
(x may be chosen from A by the remarks at the end of Definition 5.5). Since A is K-saturated,
![]() $y \in A \cap \delta $
, and hence
$y \in A \cap \delta $
, and hence
![]() $\delta \in \pi _{\mathcal {L}}[A]$
.
$\delta \in \pi _{\mathcal {L}}[A]$
.
We now show
![]() $\widehat {K}$
is correct with respect to R. Suppose
$\widehat {K}$
is correct with respect to R. Suppose
![]() $x, y \in D_2$
. If
$x, y \in D_2$
. If
![]() $x \widehat {K} y R z$
for
$x \widehat {K} y R z$
for
![]() $z \in D_2$
, then
$z \in D_2$
, then
![]() $x K y E_1 z$
, so
$x K y E_1 z$
, so
![]() $x E_1 y' K z$
by correctness of K, and hence
$x E_1 y' K z$
by correctness of K, and hence
![]() $x R y' \widehat {K} z$
. If
$x R y' \widehat {K} z$
. If
![]() $x \widehat {K} y R \alpha $
for
$x \widehat {K} y R \alpha $
for
![]() $\alpha \in D_1$
, then
$\alpha \in D_1$
, then
![]() $x R \alpha \widehat {K} \alpha $
(by definition of R). Suppose
$x R \alpha \widehat {K} \alpha $
(by definition of R). Suppose
![]() $\alpha , \beta \in D_1$
. If
$\alpha , \beta \in D_1$
. If
![]() $\alpha \widehat {K} \beta R \gamma $
for
$\alpha \widehat {K} \beta R \gamma $
for
![]() $\gamma \in D_1$
(the only possibility), then
$\gamma \in D_1$
(the only possibility), then
![]() $\alpha R \gamma \widehat {K} \gamma $
(again by definition of R). In any case,
$\alpha R \gamma \widehat {K} \gamma $
(again by definition of R). In any case,
![]() $R\widehat {K} \subseteq \widehat {K} R$
.
$R\widehat {K} \subseteq \widehat {K} R$
.
Finally, we show
![]() $\widehat {K}$
is correct with respect to E. Suppose
$\widehat {K}$
is correct with respect to E. Suppose
![]() $x, y \in D_2$
. If
$x, y \in D_2$
. If
![]() $x \widehat {K} y E z$
for
$x \widehat {K} y E z$
for
![]() $z \in D_2$
, then
$z \in D_2$
, then
![]() $x K y E_2 z$
, so
$x K y E_2 z$
, so
![]() $x E_2 y' K z$
, and hence
$x E_2 y' K z$
, and hence
![]() $x E y' \widehat {K} z$
. If
$x E y' \widehat {K} z$
. If
![]() $x \widehat {K} y E \alpha $
for
$x \widehat {K} y E \alpha $
for
![]() $\alpha \in D_1$
, then
$\alpha \in D_1$
, then
![]() $\alpha = E_2(y)$
, and
$\alpha = E_2(y)$
, and
![]() $E_2(x) \, \overline {K} \, E_2(y)$
. So
$E_2(x) \, \overline {K} \, E_2(y)$
. So
![]() $x \; E \; E_2(x) \; \widehat {K} \; \alpha $
. Suppose
$x \; E \; E_2(x) \; \widehat {K} \; \alpha $
. Suppose
![]() $\alpha , \beta \in D_1$
. If
$\alpha , \beta \in D_1$
. If
![]() $\alpha \widehat {K} \beta E z$
for
$\alpha \widehat {K} \beta E z$
for
![]() $z \in D_2$
(the only non-trivial possibility), then
$z \in D_2$
(the only non-trivial possibility), then
![]() $\beta = E_2(z)$
. So we must have
$\beta = E_2(z)$
. So we must have
![]() $z K x$
for some
$z K x$
for some
![]() $x \in \alpha $
, and hence
$x \in \alpha $
, and hence
![]() $\alpha E x \widehat {K} z$
. In any case,
$\alpha E x \widehat {K} z$
. In any case,
![]() $E\widehat {K} \subseteq \widehat {K} E$
. We conclude that
$E\widehat {K} \subseteq \widehat {K} E$
. We conclude that
![]() $\widehat {K}$
is a correct partition of
$\widehat {K}$
is a correct partition of
![]() $T(\mathfrak {F})$
.
$T(\mathfrak {F})$
.
(2) We exhibit an isomorphism
![]() $f : T(\mathfrak {F}/K) \to T(\mathfrak {F})/\widehat {K}$
. Let
$f : T(\mathfrak {F}/K) \to T(\mathfrak {F})/\widehat {K}$
. Let
![]() $f(K(x)) = K(x)$
on K-classes (i.e., the identity on the common second layer of both frames) and
$f(K(x)) = K(x)$
on K-classes (i.e., the identity on the common second layer of both frames) and
![]() $f(\overline {E_2} (K(x))) = \overline {K} (E_2(x))$
on the additional points. To check continuity, it suffices to check on clopen subsets of the top layer only (since
$f(\overline {E_2} (K(x))) = \overline {K} (E_2(x))$
on the additional points. To check continuity, it suffices to check on clopen subsets of the top layer only (since
![]() $\widehat {K}$
identifies no points across layers and f is the identity on the bottom layers); such a clopen can be identified with a
$\widehat {K}$
identifies no points across layers and f is the identity on the bottom layers); such a clopen can be identified with a
![]() $\overline {K}$
-saturated clopen U of
$\overline {K}$
-saturated clopen U of
![]() $\mathfrak {F}$
, and we have
$\mathfrak {F}$
, and we have
 $$ \begin{align*} f^{-1}(U) =& \left\{\overline{E_2}(K(x)) : E_2(x) \in U\right\} \text{ is clopen in } T(\mathfrak{F}/K) \\ \text{iff } & \left\{K(x) : E_2(x) \in U\right\} \text{ is clopen in } \mathfrak{F}/K \\ \text{iff } & \left\{x : E_2(x) \in U\right\} \text{ is clopen in } \mathfrak{F}. \end{align*} $$
$$ \begin{align*} f^{-1}(U) =& \left\{\overline{E_2}(K(x)) : E_2(x) \in U\right\} \text{ is clopen in } T(\mathfrak{F}/K) \\ \text{iff } & \left\{K(x) : E_2(x) \in U\right\} \text{ is clopen in } \mathfrak{F}/K \\ \text{iff } & \left\{x : E_2(x) \in U\right\} \text{ is clopen in } \mathfrak{F}. \end{align*} $$
The last set is precisely
![]() $\pi _{\mathcal {L}}^{-1}(U)$
, which is clopen since U is. Clearly f is surjective; for injectivity, suppose
$\pi _{\mathcal {L}}^{-1}(U)$
, which is clopen since U is. Clearly f is surjective; for injectivity, suppose
![]() $\overline {E_2}(K(x)) \neq \overline {E_2}(K(y))$
. Then
$\overline {E_2}(K(x)) \neq \overline {E_2}(K(y))$
. Then
and hence
![]() $\overline {K}(E_2(x)) \neq \overline {K}(E_2(y))$
.
$\overline {K}(E_2(x)) \neq \overline {K}(E_2(y))$
.
Since f is a continuous bijection, it remains to show it preserves and reflects the relations [Reference Esakia, Bezhanishvili and Holliday13, Proposition 1.4.15]. For R, note (checking only the cases where f is not the identity on some input):
-
•
 $K(x) \; R \; E_2(K(y)) \leftrightarrow \widehat {K}(x) \; R \; \widehat {K}(E_2(y))$
(both are always true by definition).
$K(x) \; R \; E_2(K(y)) \leftrightarrow \widehat {K}(x) \; R \; \widehat {K}(E_2(y))$
(both are always true by definition). -
•
 $E_2(K(x)) \; R \; E_2(K(y)) \leftrightarrow \widehat {K}(E_2(x)) \; R \; \widehat {K}(E_2(y))$
(similarly).
$E_2(K(x)) \; R \; E_2(K(y)) \leftrightarrow \widehat {K}(E_2(x)) \; R \; \widehat {K}(E_2(y))$
(similarly).
For E we have
Thus, f is an isomorphism of
![]() $\mathsf {MS4}$
-frames.
$\mathsf {MS4}$
-frames.
Lemma 6.13. Let
![]() $g_1, \dots , g_n \in T(\mathfrak {F})^*$
and L be the correct partition of
$g_1, \dots , g_n \in T(\mathfrak {F})^*$
and L be the correct partition of
![]() $T(\mathfrak {F})$
corresponding to the n-generated subalgebra
$T(\mathfrak {F})$
corresponding to the n-generated subalgebra
![]() $\mathfrak {B} = \langle g_1, \dots , g_n \rangle _{T(\mathfrak {F})^*}$
of
$\mathfrak {B} = \langle g_1, \dots , g_n \rangle _{T(\mathfrak {F})^*}$
of
![]() $T(\mathfrak {F})^*$
. Let K be the correct partition of
$T(\mathfrak {F})^*$
. Let K be the correct partition of
![]() $\mathfrak {F}$
corresponding to the
$\mathfrak {F}$
corresponding to the
![]() $2n$
-generated subalgebra
$2n$
-generated subalgebra
of
![]() $\mathfrak {F}^*$
. Then
$\mathfrak {F}^*$
. Then
![]() $\widehat {K} \subseteq L$
.
$\widehat {K} \subseteq L$
.
Proof. It is sufficient to show that each generator of
![]() $\mathfrak {B}$
is
$\mathfrak {B}$
is
![]() $\widehat {K}$
-saturated. Since
$\widehat {K}$
-saturated. Since
![]() $\widehat {K}$
relates no points across layers, and each
$\widehat {K}$
relates no points across layers, and each
![]() $g_i \cap D_2$
is K-saturated (as a generator of
$g_i \cap D_2$
is K-saturated (as a generator of
![]() $\mathfrak {B}'$
), we need only check that
$\mathfrak {B}'$
), we need only check that
![]() $g_i \cap D_1$
is
$g_i \cap D_1$
is
![]() $\overline {K}$
-saturated. Suppose
$\overline {K}$
-saturated. Suppose
![]() $\alpha \in g_i$
and
$\alpha \in g_i$
and
![]() $\alpha \overline {K} \beta $
. Then there are
$\alpha \overline {K} \beta $
. Then there are
![]() $x \in \alpha , y \in \beta $
with
$x \in \alpha , y \in \beta $
with
![]() $x K y$
. Evidently,
$x K y$
. Evidently,
![]() $x \in E(g_i \cap D_1) \cap D_2$
which is K-saturated (as a generator of
$x \in E(g_i \cap D_1) \cap D_2$
which is K-saturated (as a generator of
![]() $\mathfrak {B}'$
), so
$\mathfrak {B}'$
), so
![]() $y \in E(g_i \cap D_1) \cap D_2$
. That is, y is E-related to something in
$y \in E(g_i \cap D_1) \cap D_2$
. That is, y is E-related to something in
![]() $g_i \cap D_1$
, which could only be
$g_i \cap D_1$
, which could only be
![]() $\beta $
, and hence
$\beta $
, and hence
![]() $\beta \in g_i$
.
$\beta \in g_i$
.
We now adapt our translation on frames to one on varieties of algebras. For
![]() $\mathfrak {A} \in \mathbf {S5}_2$
, let
$\mathfrak {A} \in \mathbf {S5}_2$
, let
We write H, S, and P for the class operators of taking homomorphic images, subalgebras, and products, respectively. For a variety
![]() $\mathbf {V} \subseteq \mathbf {S5}_2$
, let
$\mathbf {V} \subseteq \mathbf {S5}_2$
, let
![]() $\mathbf {V}_{\text {SI}}$
be the class of s.i.
$\mathbf {V}_{\text {SI}}$
be the class of s.i.
![]() $\mathbf {V}$
-algebras, and define
$\mathbf {V}$
-algebras, and define
![]() $T(\mathbf {V})$
to be the variety generated by the translations of the s.i. members:
$T(\mathbf {V})$
to be the variety generated by the translations of the s.i. members:
It follows from Lemma 6.10 that
![]() $T(\mathbf {V})$
is generated by a class of
$T(\mathbf {V})$
is generated by a class of
![]() $\mathsf {MS4_S}[2]$
-algebras, so
$\mathsf {MS4_S}[2]$
-algebras, so
![]() $T(\mathbf {V}) \subseteq \mathbf {MS4_S}[2]$
.
$T(\mathbf {V}) \subseteq \mathbf {MS4_S}[2]$
.
Theorem 6.14.
T preserves and reflects local finiteness; that is,
![]() $\mathbf {V} \subseteq \mathbf {S5}_2$
is locally finite iff
$\mathbf {V} \subseteq \mathbf {S5}_2$
is locally finite iff
![]() $T(\mathbf {V}) \subseteq \mathbf {MS4_S}[2]$
is locally finite.
$T(\mathbf {V}) \subseteq \mathbf {MS4_S}[2]$
is locally finite.
Proof. Suppose
![]() $T(\mathbf {V})$
is locally finite, and let
$T(\mathbf {V})$
is locally finite, and let
![]() $\mathfrak {A} = \mathfrak {F}^* \in \mathbf {V}_{\text {SI}}$
be generated by
$\mathfrak {A} = \mathfrak {F}^* \in \mathbf {V}_{\text {SI}}$
be generated by
![]() $g_1, \dots , g_n$
. Then each
$g_1, \dots , g_n$
. Then each
![]() $g_i$
is a subset of
$g_i$
is a subset of
![]() $D_2 \subseteq T(\mathfrak {F})$
, and by Lemma 6.11 the operations of
$D_2 \subseteq T(\mathfrak {F})$
, and by Lemma 6.11 the operations of
![]() $\mathfrak {A}_2 \cong \mathfrak {A}$
are definable using the clopen set
$\mathfrak {A}_2 \cong \mathfrak {A}$
are definable using the clopen set
![]() $D_2$
. By assumption, there is
$D_2$
. By assumption, there is
![]() $f:\omega \to \omega $
such that the size of the subalgebra
$f:\omega \to \omega $
such that the size of the subalgebra
![]() $\langle g_1, \dots , g_n, D_2 \rangle \subseteq T(\mathfrak {A})$
is bounded by
$\langle g_1, \dots , g_n, D_2 \rangle \subseteq T(\mathfrak {A})$
is bounded by
![]() $f(n+1)$
. This subalgebra contains every element of
$f(n+1)$
. This subalgebra contains every element of
![]() $\mathfrak {A}$
. Thus,
$\mathfrak {A}$
. Thus,
![]() ${\lvert {\mathfrak {A}} \rvert }\leq f(n+1)$
. By [Reference Bezhanishvili5, Theorem 3.7(4)], we conclude that
${\lvert {\mathfrak {A}} \rvert }\leq f(n+1)$
. By [Reference Bezhanishvili5, Theorem 3.7(4)], we conclude that
![]() $\mathbf {V}$
is locally finite.
$\mathbf {V}$
is locally finite.
Suppose
![]() $\mathbf {V}$
is locally finite. To prove that
$\mathbf {V}$
is locally finite. To prove that
![]() $T(\mathbf {V})$
is locally finite, it is sufficient to show that the generating class
$T(\mathbf {V})$
is locally finite, it is sufficient to show that the generating class
![]() $\left \{T(\mathfrak {A}) : \mathfrak {A} \in \mathbf {V}_{\text {SI}}\right \}$
is uniformly locally finite (see [Reference Mal’cev, Smirnov and Taĭclin26, p. 285]). Suppose
$\left \{T(\mathfrak {A}) : \mathfrak {A} \in \mathbf {V}_{\text {SI}}\right \}$
is uniformly locally finite (see [Reference Mal’cev, Smirnov and Taĭclin26, p. 285]). Suppose
![]() $\mathfrak {B}$
is an n-generated subalgebra of
$\mathfrak {B}$
is an n-generated subalgebra of
![]() $T(\mathfrak {A})$
, corresponding to a correct partition L of
$T(\mathfrak {A})$
, corresponding to a correct partition L of
![]() $T(\mathfrak {A}_*)$
. By Lemma 6.13, there is a
$T(\mathfrak {A}_*)$
. By Lemma 6.13, there is a
![]() $2n$
-generated subalgebra
$2n$
-generated subalgebra
![]() $\mathfrak {B}' \subseteq \mathfrak {A}$
such that the corresponding correct partition K of
$\mathfrak {B}' \subseteq \mathfrak {A}$
such that the corresponding correct partition K of
![]() $\mathfrak {A}_*$
satisfies
$\mathfrak {A}_*$
satisfies
![]() $\widehat {K} \subseteq L$
. Therefore,
$\widehat {K} \subseteq L$
. Therefore,
![]() $\mathfrak {B} \subseteq T(\mathfrak {B}')$
. By assumption, we have
$\mathfrak {B} \subseteq T(\mathfrak {B}')$
. By assumption, we have
![]() $f:\omega \to \omega $
such that
$f:\omega \to \omega $
such that
![]() ${\lvert {\mathfrak {B}'}\rvert }\leq f(2n)$
. Thus, it follows from Construction 6.8 that the size of
${\lvert {\mathfrak {B}'}\rvert }\leq f(2n)$
. Thus, it follows from Construction 6.8 that the size of
![]() $T(\mathfrak {B'})$
and hence of
$T(\mathfrak {B'})$
and hence of
![]() $\mathfrak {B}$
is bounded by
$\mathfrak {B}$
is bounded by
![]() $f(2n)^2$
.
$f(2n)^2$
.
7 Conclusion and future work
We have shown that, though the Segerberg–Maksimova theorem generalizes to certain subvarieties of
![]() $\mathbf {MS4}$
, it fails drastically for
$\mathbf {MS4}$
, it fails drastically for
![]() $\mathbf {MS4}$
in general, and already in
$\mathbf {MS4}$
in general, and already in
![]() $\mathbf {MS4_S}$
. As shown in Section 6, characterizing local finiteness even in
$\mathbf {MS4_S}$
. As shown in Section 6, characterizing local finiteness even in
![]() $\mathbf {MS4_S}[2]$
is at least as hard as in
$\mathbf {MS4_S}[2]$
is at least as hard as in
![]() $\mathbf {S5}_2$
. It is then natural to ask if the problem of local finiteness in
$\mathbf {S5}_2$
. It is then natural to ask if the problem of local finiteness in
![]() $\mathbf {MS4}$
is strictly harder; i.e., would a characterization of local finiteness in
$\mathbf {MS4}$
is strictly harder; i.e., would a characterization of local finiteness in
![]() $\mathbf {S5}_2$
yield one for
$\mathbf {S5}_2$
yield one for
![]() $\mathbf {MS4}$
? We finish with an example that suggests a negative answer.
$\mathbf {MS4}$
? We finish with an example that suggests a negative answer.
The frame
![]() $T(\mathfrak {F})$
constructed in Section 6 has the property that the relativization
$T(\mathfrak {F})$
constructed in Section 6 has the property that the relativization
![]() $\mathfrak {A}_1$
to
$\mathfrak {A}_1$
to
![]() $D_1$
is a locally finite
$D_1$
is a locally finite
![]() $\mathsf {S5}^2$
-algebra, while the relativization
$\mathsf {S5}^2$
-algebra, while the relativization
![]() $\mathfrak {A}_2$
to
$\mathfrak {A}_2$
to
![]() $D_2$
is the original
$D_2$
is the original
![]() $\mathsf {S5}_2$
-algebra
$\mathsf {S5}_2$
-algebra
![]() $\mathfrak {F}^*$
. In light of Theorem 6.14, the algebra
$\mathfrak {F}^*$
. In light of Theorem 6.14, the algebra
![]() $T(\mathfrak {F})^*$
is locally finite iff
$T(\mathfrak {F})^*$
is locally finite iff
![]() $\mathfrak {A}_2$
is locally finite, which happens iff the relativization to each of the layers of
$\mathfrak {A}_2$
is locally finite, which happens iff the relativization to each of the layers of
![]() $T(\mathfrak {F})$
is locally finite. It is then natural to conjecture that the local finiteness of an
$T(\mathfrak {F})$
is locally finite. It is then natural to conjecture that the local finiteness of an
![]() $\mathsf {MS4}$
-algebra (of finite depth) is completely determined by the local finiteness of the
$\mathsf {MS4}$
-algebra (of finite depth) is completely determined by the local finiteness of the
![]() $\mathsf {S5}_2$
-algebras of the relativizations to each layer. We show this is not the case already in
$\mathsf {S5}_2$
-algebras of the relativizations to each layer. We show this is not the case already in
![]() $\mathbf {MS4_S}[3]$
. Indeed, the following figure gives an example of an
$\mathbf {MS4_S}[3]$
. Indeed, the following figure gives an example of an
![]() $\mathsf {MS4_S}[3]$
-frame
$\mathsf {MS4_S}[3]$
-frame
![]() $\mathfrak {F}$
whose relativization to each of the three layers is a locally finite
$\mathfrak {F}$
whose relativization to each of the three layers is a locally finite
![]() $\mathsf {S5}_2$
-algebra, and yet
$\mathsf {S5}_2$
-algebra, and yet
![]() $\mathfrak {F}^*$
fails to be locally finite:
$\mathfrak {F}^*$
fails to be locally finite:
Example 7.1. Let
![]() $\mathfrak {F}$
be the frame in Figure 6. Topologically,
$\mathfrak {F}$
be the frame in Figure 6. Topologically,
![]() $\mathfrak {F}$
is the disjoint union of three layers, where the topology on each layer makes the right-most point the limit point of a one-point compactification of the finite-index points with the discrete topology. An argument similar to the proof of Lemma 6.10 shows that R and E are continuous relations, and the “top rail” ensures that
$\mathfrak {F}$
is the disjoint union of three layers, where the topology on each layer makes the right-most point the limit point of a one-point compactification of the finite-index points with the discrete topology. An argument similar to the proof of Lemma 6.10 shows that R and E are continuous relations, and the “top rail” ensures that
![]() $\mathfrak {F}$
is an
$\mathfrak {F}$
is an
![]() $\mathsf {MS4}$
-frame. Clearly the R-depth of
$\mathsf {MS4}$
-frame. Clearly the R-depth of
![]() $\mathfrak {F}$
is
$\mathfrak {F}$
is
![]() $3$
.
$3$
.

Figure 6 An
![]() $\mathsf {MS4_S}[3]$
-frame
$\mathsf {MS4_S}[3]$
-frame
![]() $\mathfrak {F}$
in which the relativization to each layer is a locally finite
$\mathfrak {F}$
in which the relativization to each layer is a locally finite
![]() $\mathsf {S5}_2$
-algebra, but
$\mathsf {S5}_2$
-algebra, but
![]() $\mathfrak {F}^*$
is not locally finite.
$\mathfrak {F}^*$
is not locally finite.
Let g be the singleton set depicted in the figure and d the top layer. Then we can generate an infinite family of sets from the two clopen sets g and d as follows:
Thus,
![]() $\mathfrak {F}^*$
is not locally finite.
$\mathfrak {F}^*$
is not locally finite.
However, the relativization
![]() $\mathfrak {A}_i$
to each layer is easily seen to be a locally finite
$\mathfrak {A}_i$
to each layer is easily seen to be a locally finite
![]() $\mathsf {S5}_2$
-algebra. As remarked in the discussion preceding Lemma 6.11,
$\mathsf {S5}_2$
-algebra. As remarked in the discussion preceding Lemma 6.11,
![]() $\mathfrak {A}_1$
belongs to a proper subvariety of
$\mathfrak {A}_1$
belongs to a proper subvariety of
![]() $\mathbf {S5}^2$
, hence is locally finite. The second and third layers, equipped with the restrictions of the relations R and E, form an
$\mathbf {S5}^2$
, hence is locally finite. The second and third layers, equipped with the restrictions of the relations R and E, form an
![]() $\mathsf {S5}_2$
-frame that is a compactification of an infinite disjoint union of a single finite frame (a 3-element frame in the case of the second layer, and a singleton frame in the case of the third). Thus, for
$\mathsf {S5}_2$
-frame that is a compactification of an infinite disjoint union of a single finite frame (a 3-element frame in the case of the second layer, and a singleton frame in the case of the third). Thus, for
![]() $i \in \left \{2,3\right \}$
,
$i \in \left \{2,3\right \}$
,
![]() $\mathfrak {A}_i$
is a subalgebra of an infinite power of a single finite algebra, so
$\mathfrak {A}_i$
is a subalgebra of an infinite power of a single finite algebra, so
![]() $\mathfrak {A}_i$
belongs to a finitely generated variety, and hence
$\mathfrak {A}_i$
belongs to a finitely generated variety, and hence
![]() $\mathfrak {A}_i$
is locally finite.
$\mathfrak {A}_i$
is locally finite.
There are two natural directions of research suggested by the results in this paper. First, as was demonstrated in [Reference Bezhanishvili, Brantley and Ilin2], the monadic version of Casari’s formula plays an important role in obtaining a faithful provability interpretation of the one-variable fragment of intuitionistic predicate logic. Let
![]() $\mathsf {M^{+}S4}$
be the extension of
$\mathsf {M^{+}S4}$
be the extension of
![]() $\mathsf {MS4}$
obtained by postulating the Gödel translation of this formula. The restrictions on the interaction of the relations R and E in
$\mathsf {MS4}$
obtained by postulating the Gödel translation of this formula. The restrictions on the interaction of the relations R and E in
![]() $\mathsf {M^{+}S4}$
-frames make it plausible to expect a more manageable characterization of locally finite varieties of
$\mathsf {M^{+}S4}$
-frames make it plausible to expect a more manageable characterization of locally finite varieties of
![]() $\mathsf {M^{+}S4}$
-algebras akin the Segerberg–Maksimova theorem.
$\mathsf {M^{+}S4}$
-algebras akin the Segerberg–Maksimova theorem.
Another direction of research is suggested by the nature of the non-locally finite frames given in the paper. The
![]() $\mathsf {S5}_2$
-frame in Figure 4 and the frame in Figure 6 both exhibit a one-generated infinite subalgebra in a similar manner, by alternating through the (non-commuting) relations. It is worth investigating whether this phenomenon is the only reason for non-local finiteness in
$\mathsf {S5}_2$
-frame in Figure 4 and the frame in Figure 6 both exhibit a one-generated infinite subalgebra in a similar manner, by alternating through the (non-commuting) relations. It is worth investigating whether this phenomenon is the only reason for non-local finiteness in
![]() $\mathbf {S5}_2$
, and even in
$\mathbf {S5}_2$
, and even in
![]() $\mathbf {MS4}$
.
$\mathbf {MS4}$
.
Acknowledgments
We thank the referee for careful reading and useful feedback.