Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-13T10:59:43.986Z Has data issue: false hasContentIssue false
  • English
  • Français

Louveau's theorem for the descriptive set theory of internal sets

Published online by Cambridge University Press:  12 March 2014

Kenneth Schilling  and
Boško Živaljević
Kenneth Schilling
Affiliation:
Department of Mathematics, University of Michigan—Flint, Flint, MI 48502-2186, USA, E-mail: schilling.k@msb.flint.umich.edu
Boško Živaljević
Affiliation:
Department of Computer Science, The University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA Process Management, Computer Technology, International Paper Company, 3101 International Drive East, Mobile, AL 36606, USA, E-mail: zivaljev@cs.uiuc.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We give positive answers to two open questions from [15]. (1) For every set C countably determined over 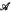, if C is 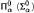then it must be 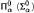over 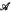, and (2) every Borel subset of the product of two internal sets X and Y all of whose vertical sections are 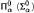can be represented as an intersection (union) of Borel sets with vertical sections of lower Borel rank. We in fact show that (2) is a consequence of the analogous result in the case when X is a measurable space and Y a complete separable metric space (Polish space) which was proved by A. Louveau and that (1) is equivalent to the property shared by the inverse standard part map in Polish spaces of preserving almost all levels of the Borel hierarchy.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 62 , Issue 2 , June 1997 , pp. 595 - 607
Copyright
Copyright © Association for Symbolic Logic 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Anderson, R. A., Star-finite representation of measure spaces, Transactions of the American Mathematical Society, vol. 271 (1982), pp. 667–87.CrossRefGoogle Scholar
[2] Henson, C. W., Analytic sets, Baire sets and the standard part map, Canadian Journal of Mathematics, vol. 31 (1979), pp. 663–672.CrossRefGoogle Scholar
[3] Henson, C. W. and Ross, D., Analytic mappings on hyperfinite sets, Proceedings of the American Mathematical Society, vol. 2 (1993), pp. 587–596.CrossRefGoogle Scholar
[4] Hurd, A. E. and Loeb, P. A., An introduction to nonstandard real analysis, Academic Press, New York, 1985.Google Scholar
[5] Keisler, H. J., Kunen, K., Miller, A., and Leth, S., Descriptive set theory over hyperfinite sets, this Journal, vol. 54 (1989), no. 4, pp. 1167–1180.Google Scholar
[6] Kunen, K. and Miller, A., Borel and projective sets from the point of view of compact sets, Mathematical Proceedings of the Cambridge Philosophical Society, vol. 94 (1983), pp. 399–409.CrossRefGoogle Scholar
[7] Louveau, A., A separation theorem for sets, Transactions of the American Mathematical Society, vol. 260 (1980), pp. 363–378.Google Scholar
[8] Render, H., private communication.Google Scholar
[9] Rogers, C. A., Analytic sets, Academic Press, New York, 1980.Google Scholar
[10] Stroyan, K. D. and Bayod, J. M., Foundations of infinitesimal stochastic analysis, North-Holland, Amsterdam, 1986.Google Scholar
[11] Živaljević, B., functions are almost internal, to appear.Google Scholar
[12] Živaljević, B., Every Borel function is monotone Borel, Annals of Pure and Applied Logic, vol. 54 (1991), pp. 87–99.CrossRefGoogle Scholar
[13] Živaljević, B., The structure of graphs all of whose Y-sections are internal sets, this Journal, vol. 56 (1991), pp. 50–66.Google Scholar
[14] Živaljević, B., Lusin-Sierpinski index for the internal sets, this Journal, vol. 57 (1992), pp. 172–178.Google Scholar
[15] Živaljević, B., Graphs with (κ) Y-sections, Archives of Mathematical Logic, vol. 32 (1993), no. 4, pp. 259–273.CrossRefGoogle Scholar