Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T18:35:13.047Z Has data issue: false hasContentIssue false
  • English
  • Français

L(Q)-preservation theorems

Published online by Cambridge University Press:  12 March 2014

Jörg Flum
Jörg Flum*
Affiliation:
Mathematisches Institut der Albert-Ludwigs-Universität, 78 Freiburg, Germany
Get access Rights & Permissions [Opens in a new window]

Extract

Much effort has been spent to prove that the reduced product operation preserves, and sometimes even strengthens the L-equivalence of structures, where L is some infinitary language. A similar result is suggested by the following well-known fact:

Assume D is a nonprincipal ultrafilter on ω and, for n Є ω, Cn is a set. If the ultra-product ΠωCn/D is infinite, it has a cardinality ≥ 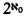Hence, by Łos' theorem, (i) if 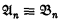and φ(x) is a first-order formula, then 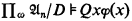iff 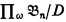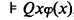where Q is the unary quantifier “there are 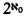many.”

We shall prove some generalizations of (i). In particular, we show

(ii) if D is a nonprincipal ultrafilter over I = ω, and 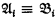then 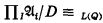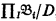where L(Q) is the language obtained from the first-order language by adding the quantifier Q.

(ii) remains true, if D is an ω-regular or an atomless filter over a set I.

Lipner [7] proved that if 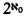is regular, then the L(Q)-equivalence is preserved under direct products. We show that the assumption “ 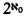is regular” is necessary.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 40 , Issue 3 , September 1975 , pp. 410 - 418
Copyright
Copyright © Association for Symbolic Logic 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Benda, M., Reduced products and non-standard logics, this Journal, vol. 34 (1969), pp. 424–436.Google Scholar
[2]Ehrenfeucht, A., An application of games to the completeness problem for formalized theories, Fundamenta Mathematicae, vol. 49 (1961), pp. 129–141.CrossRefGoogle Scholar
[3]Feferman, S. and Vaught, R., The first-order properties of algebraic systems, Fundamenta Mathematicae, vol. 47 (1959), pp. 57–103.CrossRefGoogle Scholar
[4]Flum, J., Generalized quantifiers and reduced products, Notices of the American Mathematical Society, vol. 21 (1974).Google Scholar
[5]Flum, J., On Horn theories, Mathematische Zeitschrift, vol. 138 (1974), pp. 205–212.CrossRefGoogle Scholar
[6]Keisler, H. J., Formulas with linearly ordered quantifiers, The syntax and semantics of infinitary languages, Lecture Notes in Mathematics, vol. 72 (1968), pp. 96–130.CrossRefGoogle Scholar
[7]Lipner, L. D., Some aspects of generalized quantifiers, Thesis, University of California, Berkeley, 1970.Google Scholar
[8]Skolem, T., Untersuchungen über die Axiome des Klassenkalküls und über die “Productations und Summationsprobleme”, welche gewisse Klassen von Aussagen betreffen, Skrifter utgit av Videnskapsselskapet i Kristiania, I. Klasse no. 3, Oslo 1919.Google Scholar
[9]Vinner, S., A generalization of Ehrenfeucht's game and some applications, Israel Journal of Mathematics, vol. 12 (1972), pp. 279–298.CrossRefGoogle Scholar
[10]Wojciechowska, A., Generalized products for Q-languages, Bulletin de l'Académie Polonaise des Sciences, vol. 17 (1969), pp. 337–339.Google Scholar