Article contents
Major subspaces of recursively enumerable vector spaces1
Published online by Cambridge University Press: 12 March 2014
Extract
The main point of this paper is a further development of some aspects of the recent theory of recursively enumerable (r.e.) algebraic structures. Initial work in this area is due to Frölich and Shepherdson [4] and Rabin [10]. Here we are only concerned with vector space structure. The previous work on r.e. vector spaces is due to Dekker [2], [3], Metakides and Nerode [8], Remmel [11], Retzlaff [13], and the author [5].
Our object of study is V∞ a countably infinite dimensional fully effective vector space over a countable recursive field 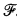 . By fully effective we mean that V∞. under a fixed Godel numbering has the following properties:
. By fully effective we mean that V∞. under a fixed Godel numbering has the following properties:
(i) Operations of vector addition and scalar multiplication on V∞ are presented by partial recursive functions on the Gödel numbers of elements of V∞.
(ii) V∞ has a dependence algorithm, i.e., there is a uniform effective procedure which applied to any n vectors of V∞ determines whether or not they are linearly independent.
We also study 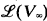 , the lattice of r.e. subspaces of V∞ (under the operations of intersection, ⋂ and (weak) sum, +). We note that if
, the lattice of r.e. subspaces of V∞ (under the operations of intersection, ⋂ and (weak) sum, +). We note that if 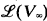 is not distributive and is merely modular (see [1]). This fact indicates the essential difference between
is not distributive and is merely modular (see [1]). This fact indicates the essential difference between 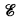 the lattice of r.e. sets and
the lattice of r.e. sets and 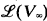 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1978
Footnotes
These results form part of the author's dissertation.
References
BIBLIOGRAPHY
- 8
- Cited by

