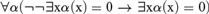Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Moschovakis, Joan Rand
2021.
Solovay’s Relative Consistency Proof for FIM and BI.
Notre Dame Journal of Formal Logic,
Vol. 62,
Issue. 4,