Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T19:13:05.292Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimal models

Published online by Cambridge University Press:  12 March 2014

Rainer Deissler
Rainer Deissler*
Affiliation:
Mathemattsches Institut der Albert-Ludwigs-Universität, 78 Freiburg, Federal Republic of Germany
Get access Rights & Permissions [Opens in a new window]

Extract

A model is called minimal if it does not contain a proper elementary submodel. A class of models is called Σ11(Π11 resp. elementary) if it is axiomatized by a sentence 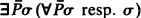with σ in 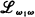and 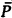some string of predicate symbols. All languages considered are assumed to be countable. For each model 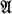we shall define in a natural way its rank, denoted by rk (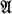), which is an ordinal or ∞. Intuitively speaking, rk (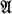) is the least upper bound for the number of steps needed to define the elements of 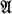by first order formulas; e.g. we shall have rk((ω, <)) = 1 (each element is f.o. definable), rk ((Z, <)) = 2 (no element is f.o. definable, each element is f.o. definable using any other element as a parameter), rk ((Q, <) ) = ∞ (no element is f.o. definable by any number of steps). This notion of rank leads to a useful game theoretic characterization of minimal models which we apply to show that the Π11 class of minimal models is not Σ11.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 42 , Issue 2 , June 1977 , pp. 254 - 260
Copyright
Copyright © Association for Symbolic Logic 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baldwin, J. T., αT is finite for ℵ1-categorical T, Transactions of the American Mathematical Society, vol. 181 (1973), pp. 37–51.Google Scholar
[2]Baldwin, J. T., Blass, A. R., Glass, A. M. and Kueker, D. W., A “natural” theory without a prime model, Algebra Universalis, vol. 3 (1973), pp. 152–155.Google Scholar
[3]Baldin, J. T. and Lachlan, A. H., On strongly minimal sets, this Journal, vol. 36 (1971), pp. 79–96.Google Scholar
[4]Chang, C. C. and Keisler, H. J., Model theory, North-Holland, Amsterdam, 1973.Google Scholar
[5]Deissler, R., Untersuchungen iiber Minimalmodelle, Dissertation, University of Freiburg, 1974.Google Scholar
[6]Flum, J., First-order logic and its extensions, Logic Conference, Kiel, 1974, Springer, Berlin, 1975.Google Scholar
[7]Lopez-Escobar, E. G. K., On defining well ordering, Fundamenta Mathematicae, vol. 59 (1966), pp. 13–21.CrossRefGoogle Scholar
[8]Vaught, R. L., Descriptive set theory in Lω1ω, Cambridge Summer School in Mathematical Logic, Springer, Berlin, 1973, pp. 574–598.Google Scholar