Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T17:43:35.520Z Has data issue: false hasContentIssue false
  • English
  • Français

A minimal pair of Π10 classes1

Published online by Cambridge University Press:  12 March 2014

Carl G. Jockusch Jr  and
Robert I. Soare
Carl G. Jockusch Jr
Affiliation:
University of Illinois, Urbana
Robert I. Soare
Affiliation:
University of Illinois at Chicago Circle
Get access Rights & Permissions [Opens in a new window]

Extract

A pair of sets (A0, A1) forms a minimal pair if A0 and A1 are nonrecursive, and if whenever a set B is recursive both in A0 and in A1 then B is recursive. C. E. M. Yates [8] and independently A. H. Lachlan [4] proved the existence of a minima] pair of recursively enumerable (r.e.) sets thereby establishing a conjecture of G. E. Sacks [6]. We simplify Lachlan's construction, and then generalize this result by constructing two disjoint pairs of r.e. sets (A0, B0) and (A1B1) such that if C0 separates (A0, A1 and C1 separates (B0, B1), then C0 and C1 form a minimal pair. (We say that C separates (A0, A1) if A0 ⊂ C and C ∩ = ∅.) The question arose in our study of (Turing) degrees of members of certain 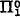classes, where we proved the weaker result [2, Theorem 4.1] that the above pairs may be chosen so that C0 and C2 are merely Turing incomparable. (There we used a variation of the weaker result to improve a result of Scott and Tennenbaum that no complete extension of Peano arithmetic has minimal degree.)

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 36 , Issue 1 , March 1971 , pp. 66 - 78
Copyright
Copyright © Association for Symbolic Logic 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

This problem arose from our study [2] of degrees of models and theories, a problem area which was suggested to us by A. H. Lachlan. G. E. Sacks brought to our attention H. Friedman's work [1] on hyperdegrees of members of classes, and asked us what analogous results held for Turing degrees of members of recursively bounded classes. This research was supported by National Science Foundation Grants GP 7421 and GP 8866.

References

[1]Friedman, H., Borel sets and hyperdegrees (to appear).Google Scholar
[2]Jockusch, C. G. Jr., and Soare, R. I., Π10 classes and degrees of theories (to appear).Google Scholar
[3]Jockusch, C. G. Jr., and Soare, R. I., Degrees of members of Π10 classes (to appear).Google Scholar
[4]Lachlan, A. H., Lower bounds for pairs of r.e. degrees, Proceedings of the London Mathematical Society (3), vol. 16 (1966), pp. 537–569.CrossRefGoogle Scholar
[5]Rogers, H. Jr., Theory of recursive functions and effective computabttity, McGraw-Hill, New York, 1967.Google Scholar
[6]Sacks, G. E., Degrees of unsolvability, Annals of mathematics studies No. 55, Princeton Univ. Press, Princeton, N.J., 1963.Google Scholar
[7]Shoenheld, J. R., Degrees of models, this Journal, vol. 25 (1960), pp. 233–237.Google Scholar
[8]Yates, C. E. M., A minimal pair of r.e. degrees, this Journal, vol. 31 (1966), pp. 159–168.Google Scholar