Article contents
Mixed systems
Published online by Cambridge University Press: 12 March 2014
Extract
In [A1]–[A4] there is an abstract description, in terms of “α-systems”, of the object of a nested priority construction, and there is a metatheorem listing conditions which guarantee the success of the construction. The metatheorem has different versions, with later versions becoming simpler and more general. The information needed to meet the requirements is enumerated by a 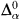 function, where α is an arbitrary recursive ordinal. All other objects associated with the α-system are r.e. In the basic metatheorem, the requirements must all be at level α, although there is a special result, for limit α, which allows one requirement at each level in an increasing sequence with limit α. There are other abstract descriptions of nested priority arguments in [K1], [K2], [K3], and [L-L].
function, where α is an arbitrary recursive ordinal. All other objects associated with the α-system are r.e. In the basic metatheorem, the requirements must all be at level α, although there is a special result, for limit α, which allows one requirement at each level in an increasing sequence with limit α. There are other abstract descriptions of nested priority arguments in [K1], [K2], [K3], and [L-L].
A typical use of α-systems is that in [B], where it is shown that, for a relation R on a recursive structure 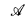 , under suitable assumptions, if R does not have a “recursive Σα” definition in
, under suitable assumptions, if R does not have a “recursive Σα” definition in 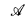 , then there is a recursive isomorphic copy of
, then there is a recursive isomorphic copy of 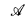 in which the image of R is not
in which the image of R is not  . There is no difficulty in generalizing this to make each of infinitely many relations not
. There is no difficulty in generalizing this to make each of infinitely many relations not  , when the assumptions are uniformly satisfied and each relation has no recursive Σα definition. However, the metatheorems for α-systems do not apply to the situation where we have several (even two) relations Ri, which do not have recursive Σβi definitions and whose images we wish to make not
, when the assumptions are uniformly satisfied and each relation has no recursive Σα definition. However, the metatheorems for α-systems do not apply to the situation where we have several (even two) relations Ri, which do not have recursive Σβi definitions and whose images we wish to make not 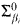 for distinct βi. An even more basic problem is to construct a recursive copy of a recursive structure via an isomorphism whose restriction to various sets Ui, is not
for distinct βi. An even more basic problem is to construct a recursive copy of a recursive structure via an isomorphism whose restriction to various sets Ui, is not 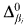 If βi, = α for all i, then we can use an (α + 1)-system; otherwise, the old metatheorems do not apply.
If βi, = α for all i, then we can use an (α + 1)-system; otherwise, the old metatheorems do not apply.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1994
References
REFERENCES
- 6
- Cited by

