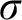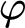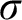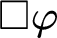Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Berger, Sören
Block, Alexander Christensen
and
Löwe, Benedikt
2023.
The modal logic of abelian groups.
Algebra universalis,
Vol. 84,
Issue. 3,
Löwe, Benedikt
and
Xiao, Han
2025.
Logic and Its Applications.
Vol. 15402,
Issue. ,
p.
164.