Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T10:25:24.774Z Has data issue: false hasContentIssue false
  • English
  • Français

THE MODAL LOGICS OF KRIPKE–FEFERMAN TRUTH

Part of: General logic

Published online by Cambridge University Press:  27 October 2020

CARLO NICOLAI  and
JOHANNES STERN
CARLO NICOLAI
Affiliation:
DEPARTMENT OF PHILOSOPHY KING’S COLLEGE LONDONLONDON, UKE-mail: carlo.nicolai@kcl.ac.uk
JOHANNES STERN
Affiliation:
DEPARTMENT OF PHILOSOPHY UNIVERSITY OF BRISTOL BRISTOL, UKE-mail: johannes.stern@bristol.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We determine the modal logic of fixed-point models of truth and their axiomatizations by Solomon Feferman via Solovay-style completeness results. Given a fixed-point model $\mathcal {M}$ , or an axiomatization S thereof, we find a modal logic M such that a modal sentence 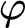$\varphi $ is a theorem of M if and only if the sentence 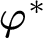$\varphi ^*$ obtained by translating the modal operator with the truth predicate is true in $\mathcal {M}$ or a theorem of S under all such translations. To this end, we introduce a novel version of possible worlds semantics featuring both classical and nonclassical worlds and establish the completeness of a family of noncongruent modal logics whose internal logic is nonclassical with respect to this semantics.

Keywords

axiomatic theories of truthsemantic theoriesmodal logicnon-classical logicmany-valued logicprovability logicliar paradoxSolovay completenessKripke’s theory of truthKripke-Feferman truth.

MSC classification

Secondary: 03B45: Modal logic (including the logic of norms) 03B50: Many-valued logic
Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 1 , March 2021 , pp. 362 - 396
Check for updates
Copyright
© The Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aczel, P., Frege structures and the notions of proposition, truth and set, The Kleene Symposium, Studies in Logic and the Foundations of Mathematics, vol. 101, North-Holland, Amsterdam-New York, 1980, pp. 31–59.10.1016/S0049-237X(08)71252-7CrossRefGoogle Scholar
Anderson, A. R. and Belnap, N. D., Entailment: The Logic of Relevance and Neccessity, vol. I, Princeton University Press, Princeton, NJ, 1975. Google Scholar
Blackburn, P., de Rijke, M., de Venema, Y., Modal Logic, Cambridge Tracts in Theoretical Computer Science, vol. 53, Cambridge University Press, Cambridge, 2001.10.1017/CBO9781107050884CrossRefGoogle Scholar
Burgess, J. P., Friedman and the axiomatization of Kripke’s theory of truth, Foundational Adventures, Tributes, vol. 22, Colloquium Publications, London, 2014, pp. 125–148.Google Scholar
Buss, S., Bounded Arithmetic, Bibliopolis, Napoli, 1986.Google Scholar
Cain, J. and Damnjanovic, Z., On the weak Kleene scheme in Kripke’s theory of truth, this Journal, vol. 56 (1991), no. 4, pp. 1452–1468.Google Scholar
Cantini, A., Notes on formal theories of truth. Zeitschrift für Logik und Grundlagen der Mathematik, vol. 35 (1989), pp. 97–130.CrossRefGoogle Scholar
Castaldo, L. and Stern, J., KF, PKF, and Reinhardt’s Program, preprint, 2020, arXiv:2005.01054.Google Scholar
Chellas, B. F., Modal Logic, Cambridge University Press, Cambridge-New York, 1980.CrossRefGoogle Scholar
Coniglio, M. and Corbalan, M., Sequent calculi for the classical fragment of Bochvar and Halldén’s nonsense logics. Electronic Proceedings in Theoretical Computer Science, vol. 113 (2013), no. 03, 125.CrossRefGoogle Scholar
Czarnecki, M. and Zdanowski, K., A modal logic of a truth definition for finite models. Fundamenta Informaticae, vol. 164 (2019), no. 4, pp. 299–325.CrossRefGoogle Scholar
Da Costa, N. C. A., On the theory of inconsistent formal systems. Notre Dame Journal of Formal Logic, vol. 15 (1974), no. 4, pp. 497–510.10.1305/ndjfl/1093891487CrossRefGoogle Scholar
Feferman, S., Towards useful type-free theories I, this Journal, vol. 49 (1984), no. 1, pp. 75–111.Google Scholar
Feferman, S., Reflecting on incompleteness, this Journal, vol. 56 (1991), pp. 1–49.Google Scholar
Feferman, S., Axioms for determinateness and truth. Review of Symbolic Logic, vol. 1 (2008), no. 2, pp. 204–217.CrossRefGoogle Scholar
Fischer, M., Halbach, V., Kriener, J., and Stern, J., Axiomatizing semantic theories of truth? The Review of Symbolic Logic, vol. 8 (2015), no. 2, pp. 257–278.CrossRefGoogle Scholar
Friedman, H. and Sheard, M., An axiomatic approach to self-referential truth. Annals of Pure and Applied Logic, vol. 33 (1987), no. 1, pp. 1–21.CrossRefGoogle Scholar
Fujimoto, K., Relative truth definability of axiomatic truth theories. Bulletin of Symbolic Logic, vol. 16 (2010), no. 3, pp. 305–344.CrossRefGoogle Scholar
Gupta, A. and Belnap, N., The Revision Theory of Truth, MIT Press, Cambridge, MA, 1993.10.7551/mitpress/5938.001.0001CrossRefGoogle Scholar
Hájek, P. and Pudlák, P., Metamathematics of First-Order Arithmetic, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1998.Google Scholar
Halbach, V., A system of complete and consistent truth. Notre Dame Journal Formal Logic, vol. 35 (1994), no. 3, pp. 311–327.CrossRefGoogle Scholar
Halbach, V., Axiomatic Theories of Truth, Revised edition, Cambridge University Press, Cambridge, 2014.10.1017/CBO9781139696586CrossRefGoogle Scholar
Halbach, V. and Horsten, L., Axiomatizing Kripke’s theory of truth in partial logic, this Journal, vol. 71 (2006), pp. 677–712.Google Scholar
Jaspars, J. and Thijsse, E., Fundamentals of partial modal logic, Partiality, Modality, Nonmonotonicity (Doherty, P., editor), CSLI, Stanford, 1996, pp. 111–141. Google Scholar
Kleene, S. C., Introduction to Metamathematics, North Holland, Amsterdam, 1952.Google Scholar
Kripke, S., Outline of a theory of truth, Journal of Philosophy, vol. 72 (1975), pp. 690–712.CrossRefGoogle Scholar
Loeb, M. H., Solution of a problem of Leon Henkin, this Journal, vol. 20 (1955), pp. 115–118.Google Scholar
Martin, R. L. and Woodruff, P. W., On representing ‘true-in-L’ in L, Recent Essays on Truth and the Liar Paradox (Martin, R. L., editor), Oxford University Press, Oxford, 1984, p. 47.Google Scholar
Moschovakis, Y. N., Elementary Induction on Abstract Structures, Studies in Logic and the Foundations of Mathematics, vol. 77, North-Holland, 1974.Google Scholar
Nicolai, C., Provably true sentences across axiomatizations of Kripke’s theory of truth. Studia Logica, vol. 106 (2018), no. 1, pp. 101–130.CrossRefGoogle Scholar
Nicolai, C. and Stern, J., First-order modal logics of truth. Unpublished Manuscript, 2020.Google Scholar
Odintsov, S. P. and Wansing, H., Modal logics with Belnapian truth values. Journal of Applied Non-Classical Logics, vol. 20 (2010), no. 3, pp. 279–301.CrossRefGoogle Scholar
Odintsov, S. P. and Speranski, S. O, The lattice of Belnapian modal logics: special extensions and counterparts. Logic and Logical Philosophy, vol. 25 (2016), no. 1, pp. 3–33.Google Scholar
Odintsov, S. P. and Speranski, S. O., Belnap–Dunn modal logics: Truth constants vs. truth values. The Review of Symbolic Logic, vol. 13 (2020), no. 2, pp. 416–435.CrossRefGoogle Scholar
Pakhomov, F., Solovay’s completeness without fixed points, Logic, Language, Information, and Computation, Lecture Notes in Computer Science, vol. 10388, Springer, Berlin, 2017, pp. 281–294.CrossRefGoogle Scholar
Priest, G., An Introduction to Non-Classical Logic: From If to Is, Cambridge University Press, Cambridge, 2008.CrossRefGoogle Scholar
Segerberg, K., An Essay in Classical Modal Logic. Filosofiska Studier, vol. 13, Filosofiska Föreningen och Filosofiska Institutionen vid Uppsala Universitet, Uppsala, 1971.Google Scholar
Smoryński, C., Self-Reference and Modal Logic. Springer-Verlag, New York, 1985.CrossRefGoogle Scholar
Solovay, R. M., Provability interpretations of modal logic. Israel Journal of Mathematics, vol. 25 (1976), no. 3–4, pp. 287–304.CrossRefGoogle Scholar
Speranski, S. O., Notes on the computational aspects of Kripke’s theory of truth. Studia Logica, vol. 105 (2017), no. 2, pp. 407–429.CrossRefGoogle Scholar
Standefer, S., Solovay-type theorems for circular definitions. Review of Symbolic Logic, vol. 8 (2015), no. 3, pp. 467–487.CrossRefGoogle Scholar
Stern, J., Toward Predicate Approaches to Modality, vol. 44. Springer, New York, 2015.Google Scholar
Tarski, A., A lattice-theoretical fixpoint theorem and its applications. Pacific Journal of Mathematics, vol. 5 (1955), pp. 285–309.CrossRefGoogle Scholar
Tarski, A., Der Wahrheitsbegriff in den formalisierten Sprachen, Logic, Semantics, Metamathematics, Clarendon Press, Oxford, 1956, pp. 152–278.Google Scholar
Visser, A., Semantics and the liar paradox, Handbook of Philosophical Logic (Gabbay, D. and Guenthner, F., editors), Springer, New York, pp. 617–706.Google Scholar